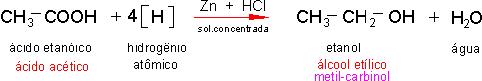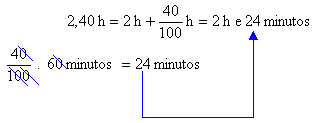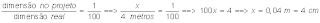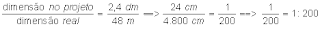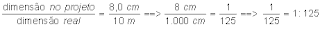Escala
Definimos escala de um desenho como sendo a razão entre o comprimento do projeto e o comprimento real correspondente,
sempre medidos na mesma unidade.

Usamos escala quando queremos representar um esboço gráfico de objetos, da planta de uma casa ou de uma cidade, mapas,
maquetes, etc.
Se num mapa a escala indicada é de 1 : 1000, isso quer dizer que cada medida no desenho do mapa é 1000 vezes menor que a
realidade, sendo assim : Cada 1 cm medido no mapa representará no real ->1000 cm = 10 m
Se num projeto arquitetônico cada cm desenhado equivale a 120 cm ( 1,2 m ) de dimensão real, afirmamos que esse modelo está
na escala de 1 : 120, ou seja, tudo na realidade é 120 vezes maior que no projeto arquitetônico.
Se num aeromodelo cada cm do protótipo equivale a 32 cm no real, afirmamos que esse modelo está na escala de 1 : 32, ou seja,
tudo no avião é 32 vezes maior que no modelo.
Todo mapa cartográfico é feito em escala
Todo projeto arquitetônico é feito em escala
Toda maquete reproduz fielmente o real, já que sempre é projetada em escala


Ambas as casas estão desenhadas em escala. A moça que aparece a frente da casa rosa tem, por definição em projetos de
arquitetura, a altura de 1,70 m. Assim se tem uma idéia melhor das dimensões da casa.

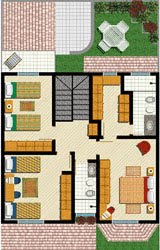
Outros dois projetos, também executados em escala.
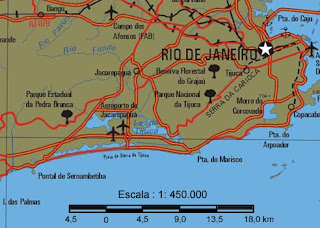
O Mapa parcial do município do Rio de Janeiro está construído na escala 1:450.000, ou seja, cada cm medido no mapa, medirá,
na verdade 450.000 vezes maior, ou seja : 1 cm no mapa será equivalente, no mapa, a 450.000 cm = 4.500 m = 4,5 km.
Escala - Exercícios Resolvidos
Exemplo 01) Um protótipo foi desenhado na escala 1:100. Qual será o comprimento desse protótipo se o modelo em tamanho real tem
um comprimento igual a 4,00 m ? 4 cm
Resolução : Os exercícios de escalas sempre serão resolvidos por meio de proporção. Se a escala é de 1:100, podemos escrever :
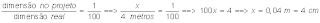
Exemplo 02) Qual é escala da planta de um terreno no qual um comprimento de 48 metros foi representado no papel por um segmento
de 2,4 dm ?
Resolução : Já sabemos que escala é a razão entre a dimensão de projeto e a dimensão verdadeira. Assim, podemos escrever :
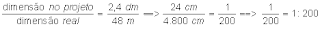
Exemplo 03) Uma bandeira brasileira oficial tem o comprimento de 10 metros e a largura de 7 metros. Que escala estaremos
trabalhando ao desenharmos nossa bandeira com 8 cm de comprimento ?
Resolução : Como escala é a razão entre a dimensão de projeto e a dimensão verdadeira. Assim, podemos escrever :
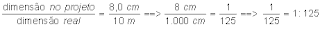
Escala - Exercícios Propostos
01) Qual deve ser a escala de uma planta de uma parede de 17,5 m, que está representada por um segmento de 0,35 dm ?
02) A distância entre duas cidades é de 150 km e está representada em um mapa por 10 cm. Determine a escala desse mapa.
03) A extensão de uma estrada de ferro é de 420 km. Qual foi a escala usada, se a mesma foi representada por 5 cm ?
04) Numa planta elaborada na escala de 1:25 a sala de jantar está com as seguintes dimensões: 12,6 cm e 1,74 dm. Calcule,
em metros quadrados, a área real da sala.
05) Em um mapa de escala 1 : 4.500.000, a distância entre duas cidades é de 100 mm. Qual será a escala de um outro mapa, no qual
estas mesmas cidades distem 2 cm entre si ?
06) Num desenho cuja escala é 1 : 500, tem-se um comprimento de 9 em, que no natural mede 45 metros. Calcule, em centímetros, o
mesmo comprimento do desenho na escala 1 :200.
07) Numa planta na escala 1 : 1.000, que dimensões (em m) devem ser atribuídas, a um compartimento de 0,5 dm por 60 mm ?
08) Qual o comprimento que devemos representar uma avenida de 42 hm de comprimento, ao desenhar a planta de um bairro, na
escala de 1 : 20.000 ?
09) Num mapa, uma rua mede 72 cm. Calcule o comprimento natural da rua, sabendo-se que o mapa foi desenhado na escala de
1 : 250.
10) Um prédio está desenhado na escala 1 : 150. Qual é o perímetro e a área de uma sala, que no desenho mede 4 cm x 5 cm ?
11) Sabe-se que um terreno tem 8.400 m2. Para representá-la por um retângulo de 6 cm por 2 cm, que escala deveremos representar?
Escala - Exercícios - Questões Objetivas
12) Um muro de 28,5 m está representado num desenho na escala 1 : 75. O comprimento do muro desenhado, é:
a) 0,38 m b) 0,38 cm c) 3,8 cm d) 1,9 m e) 0,19 dm
13) Num mapa de escala 1 : 2.000.000, a distância entre duas cidades é de 10 cm. Qual a distância entre as cidades ?
a) 10 km b) 20 km c) 100 km d) 200 km
14) Numa carta geográfica, a distância entre as cidades A e B é de 10 em. A distância real entre elas é de 500 km. Qual é a escala
da carta ?
a) 1 : 100.000 b) 1 : 500.000 c) 1 : 1.000.000 d) 1 : 5.000.000
15) ( UFCE ) Em um mapa cartográfico, 4 cm representam 12 km. Nesse mesmo mapa, 10 cm representarão quantos quilômetros ?
a) 60 km b) 30 km c) 15 km d) 18 km e) 25 km
16) ( UNICAMP - SP ) Na planta de um edifício em construção, cuja escala é 1 : 50. As dimensões de uma sala retangular são
10 cm e 8 cm. Calcule a área total da sala projetada.
a) 20 m2 b) 22 m2 c) 25 m2 d) 36 m2 e) 42 m2
Escala - Respostas dos Exercícios Propostos
01 1:500 02 1:1.500.000 03 1:840.000 04 13,7025 m2
05 1 : 2.250.000 06 18 m 07 50 m e 60 m 08 0,21 m = 21 cm
09 180 m 10 27 m e 45 m2 11 1:3.000 12 letra A
13 letra D 14 letra D 15 Letra B 16 Letra A
/www.matematicamuitofacil.com/
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
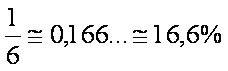



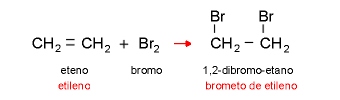
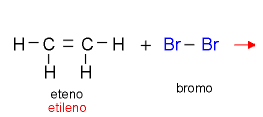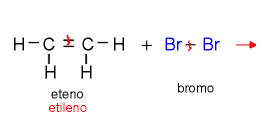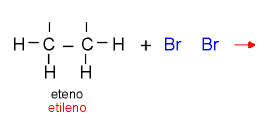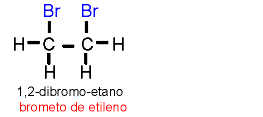
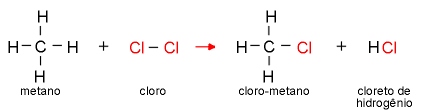
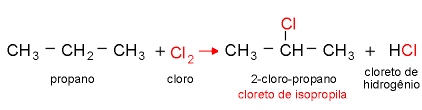 03 - Reação de eliminação: quando átomos ou radicais são eliminados da molécula orgânica.
03 - Reação de eliminação: quando átomos ou radicais são eliminados da molécula orgânica. 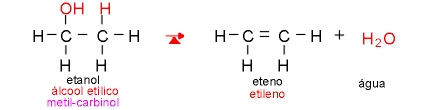 Regra de Saytzeff: Nas reações de eliminação, o hidrogênio preso ao carbono menos hidrogenado é mais facilmente eliminado.
Regra de Saytzeff: Nas reações de eliminação, o hidrogênio preso ao carbono menos hidrogenado é mais facilmente eliminado. 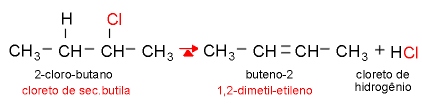


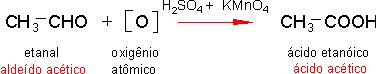

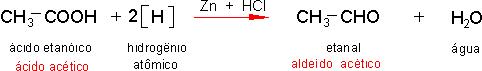
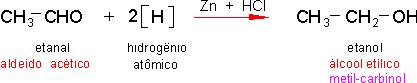
 5.4 - Redução total de ácido orgânico.
5.4 - Redução total de ácido orgânico.