Sistema Respiratório - Exercícios resolvidos
01. (UECE) Nos mamíferos, incluindo o homem, o percurso do ar inspirado, nos pulmões é:
a) bronquíolos ® brônquios ® alvéolos;
b) brônquios ® bronquíolos ® alvéolos;
c) alvéolos ® brônquios ® bronquíolos;
d) bronquíolos ® alvéolos ® brônquios.
e) n.d.a.
Resposta: B
02. Qual é a diferença entre o sangue venoso e o arterial?
ResoLUÇÃO: O venoso é pobre em oxigênio e rico em bicarbonato. O arterial é rico em oxigênio, formando oxiemoglobina.
03. (UNESP) Vários atletas do continente americano foram convidados a participar de uma competição de atletismo na cidade do Rio de Janeiro. Assim que os atletas desembarcaram no Aeroporto Internacional, eram submetidos a vários testes e exames, um dos quais o hemograma. Um determinado atleta tendo perdido seu passaporte durante a viagem, alegou ser mexicano e que morava na Cidade do México.
a) Qual o elemento figurado do sangue que, analisado através do hemograma deste atleta, possibilita acreditar na sua
origem?
b) Justifique sua resposta.
ResoLUÇÃO: a) Hemácia
b) Indivíduos provenientes de regiões de elevada altitude possuem um número maior de hemácias, para
compensar a baixa pressão parcial do O2, nessas regiões onde o ar é rarefeito.
04. (FUVEST) Jogadores de futebol que vive em altitudes próximas ao nível do mar sofrem adaptações quando jogam em cidades de grande altitude. Algumas adaptações são imediatas, outras só ocorrem após uma permanência de pelo menos três semanas. Qual alternativa inclui as realizações imediatas e as que podem ocorrer em longo prazo?
a) aumentam a freqüência respiratória, os batimentos cardíacos e a pressão arterial, em longo prazo diminui
o número de hemácias;
b) diminuem a freqüência respiratória e os batimentos cardíacos; diminui a pressão arterial, em longo prazo
aumenta o número de hemácias
c) aumentam a freqüência respiratória e os batimentos cardíacos; diminui a pressão arterial em longo prazo
diminui o número de hemácias;
d) aumentam a freqüência respiratória, os batimentos cardíacos e a pressão arterial, em longo prazo aumenta
o número de hemácias;
e) diminuem a freqüência respiratória, os batimentos cardíacos e a pressão arterial, em longo prazo aumenta
o número de hemácias.
Resposta: D
05. Por que a inalação do monóxido de carbono pode ocasionar até a morte?
ResoLUÇÃO: Ele se combina com a hemoglobina, formando carboxiemoglobina, composto estável que não transporta mais o
oxigênio.
06. O que é fosforilação oxidativa?
RESOLUÇÃO: Síntese de ATP (adenosina trifosfato) utilizando energia obtida nas oxidações celulares.
07. Quais são os processos básicos da respiração aeróbia de uma molécula de glicose?
RESOLUÇÃO: Glicólise, ciclo de Krebs, cadeia respiratória ou transportadora de elétrons.
08. Qual é a equação geral da respiração aeróbia de uma molécula de glicose?
RESOLUÇÃO: C6H12O6 + 6O2 + 6H2Og 6CO2 + 12H2O +
Segundo muitos bioquímicos, o lucro energético seria de 38ATP. Outros acreditam ser de 36ATP.
09. Quem é o aceptor final de hidrogênio na respiração celular?
RESOLUÇÃO: É o oxigênio. Ele se une ao hidrogênio, formando água.
10. Onde ocorre o ciclo do ácido cítrico?
RESOLUÇÃO: Na matriz mitocondrial.
www.colaweb.com
Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
sexta-feira, 29 de novembro de 2019
Fatoração
Fatorar uma expressão algébrica é modificar sua forma de soma algébrica para produto; fatorar uma expressão é obter outra expressão que
a) seja equivalente à expressão dada;
b) esteja na forma de produto. Na maioria dos casos, o resultado de uma fatoração é um produto notável.
Há diversas técnicas de fatoração que estudaremos em seguida, supondo a, b, x e y expressões não fatoráveis.
a) seja equivalente à expressão dada;
b) esteja na forma de produto. Na maioria dos casos, o resultado de uma fatoração é um produto notável.
Há diversas técnicas de fatoração que estudaremos em seguida, supondo a, b, x e y expressões não fatoráveis.
A. Fator Comum
Devemos reconhecer o fator comum, seja ele numérico, literal ou misto; em seguida colocamos em evidência esse fator comum, simplificamos a expressão deixando em parênteses a soma algébrica.
Observe os exemplos abaixo.
Observe os exemplos abaixo.
B. Agrupamento
Devemos dispor os termos do polinômio de modo que formem dois ou mais grupos entre os quais haja um fator comum, em seguida, colocar o fator comum em evidência.
Observe:
Observe:

C. Diferença de Quadrados
Utilizamos a fatoração pelo método de diferença de quadrados sempre que dispusermos da diferença entre dois monômios cujas literais tenham expoentes pares. A fatoração algébrica de tais expressões é obtida com os seguintes passos:
1º) Extraímos as raízes quadradas dos fatores numéricos de cada monômio;
2º) Dividimos por dois os expoentes das literais;
3º) Escrevemos a expressão como produto da soma pela diferença dos novos monômios assim obtidos.
Por exemplo, a expressão a2 – b2 seria fatorada da seguinte forma
1º) Extraímos as raízes quadradas dos fatores numéricos de cada monômio;
2º) Dividimos por dois os expoentes das literais;
3º) Escrevemos a expressão como produto da soma pela diferença dos novos monômios assim obtidos.
Por exemplo, a expressão a2 – b2 seria fatorada da seguinte forma
D. Trinômio Quadrado Perfeito
Uma expressão algébrica pode ser identificada como trinômio quadrado perfeito sempre que resultar do quadrado da soma ou diferença entre dois monômios.
Por exemplo, o trinômio x4 + 4 x2 + 4 é quadrado perfeito, uma vez que corresponde a (x2 + 2)2 .
São, portanto, trinômios quadrados perfeitos todas as expressões da forma a2 ± 2ab + b2, fatoráveis nas formas seguintes:
Por exemplo, o trinômio x4 + 4 x2 + 4 é quadrado perfeito, uma vez que corresponde a (x2 + 2)2 .
São, portanto, trinômios quadrados perfeitos todas as expressões da forma a2 ± 2ab + b2, fatoráveis nas formas seguintes:

E. Trinômio Quadrado da Forma ax2 + bx + c
Supondo sejam x1 e x2 as raízes reais do trinômio,  , dizemos que:
, dizemos que:
Lembre-se de que as raízes de uma equação de segundo grau podem ser calculadas através da fórmula de Bhaskara:
F. Soma de diferença de cubos
Se efetuarmos o produto do binômio a + b pelo trinômio a2 – ab + b2, obtemos o seguinte desenvolvimento:
O que acabamos de desenvolver foram produtos notáveis que nos permitem concluir que, para fatorarmos uma soma ou diferença de cubos, basta-nos inverter o processo anteriormente demonstrado.
Assim, dizemos que:
Fatoração

Casos Simples de Fatoração Algébrica
Como já aprendemos na Aritmética, todo número, não primo, pode ser decomposto em um produto de fatores primos. Assim, tem-se
30 = 2 X 3 X 5 ; 72 = 8 x 9 = 2 x 2 x 2 x 3 x 3 = 23 x 32
Da mesma forma, podemos decompor algumas expressões algébricas em fatores.
Assim, por exemplo : a2 - b2 = (a+b) (a - b) ; a2 + 2ab + b2 = (a + b)2 ; 12a2b3 - 18ab2 = 6ab2(2ab - 3)
O processo pelo qual transformamos uma adição algébrica em um produto algébrico denominamos fatoração algébrica, ou
simplesmente, fatoração.
No estudo da fatoração são conhecidos vários casos. Vamos estudá-los, classificando-os, para uma melhor compreensão.
Primeiro Caso de Fatoração : Evidenciação
Consideremos o polinômio 6ax2 - 4ax3 + 2ax, que pode ser escrito como :
(2ax).(3x) - (2ax).(2x) + (2ax).(1). Percebemos que o fator 2ax esta presente em todos os termos do polinômio. 2ax é o fator comum e
deverá ser colocado em evidência. Assim :
6ax2 - 4ax3 + 2ax = (2ax) (3x - 2x2 + 1)
Exemplo 01) Fatorar o polinômio 7m2p4 - 14m3p2 + 21m4p3
Colocando o fator comum 7m2p2 em evidência, teremos :
7m2p4 - 14m3p2 + 21m4p3 = 7m2p2 ( p2 - 2m + 3m2p)
Exemplo 02) Fatorar o polinômio 2m3(a - b) + 8m2( a - b)
Colocando o fator comum 2m2(a - b) em evidência, teremos :
2m3(a - b) + 8m2( a - b ) = [2m2(a - b)] ( m + 4) = 2m2(a - b)( m + 4)
Segundo Caso de Fatoração : Trinômio Quadrado Perfeito
Já aprendemos em produtos notáveis que :
(a + b)2 = a2 + 2ab + b2 e (a - b)2 = a2 - 2ab + b2
O que faremos agora é transformarmos a soma algébrica a2 ± 2ab + b2 em sua forma fatorada (a ± b)2.
E para tal precisamos compreender que um trinômio será quadrado perfeito quando possuir dois de seus três termos quadrados e o
terceiro sendo igual ao dobro do produto entre as raízes quadradas dos termos quadrados.
Exemplo 03) Se possível, fatore o polinômio 4m2 + 12mn2 + 9n4
O polinômio possui dois termos quadrados 4m2 e 9n4, e cujas raízes quadradas são, respectivamente, 2m e 3n2. O dobro do
produto entre essas raízes é exatamente igual ao terceiro termo 12mn2.
E dessa forma o polinômio 4m2 + 12mn2 + 9n4 é um trinômio quadrado perfeito e pode, portanto ser fatorado.
A raiz quadrada do primeiro termo quadrado é 2m, a raiz do segundo termo quadrado é 3n2 e o sinal que os une será o sinal do
terceiro termo + 12mn2. Dessa forma, teremos :
4m2 + 12mn2 + 9n4 = ( 2m + 3n2)2
Exemplo 04) Se possível, fatore o polinômio 16x4 + 36x2y3 + 25y6
O polinômio possui dois termos quadrados 16x4 e 25y6, e cujas raízes quadradas são, respectivamente, 4x2 e 5y3. O dobro do produto
entre essas raízes é igual a 40x2y3 que é diferente do terceiro termo 36x2y3.
E dessa forma o polinômio 16x4 + 36x2y3 + 25y6 não é um trinômio quadrado perfeito e não pode, portanto, ser fatorado, pelo menos
como um trinômio quadrado perfeito.
Exemplo 05) Se possível, fatore o polinômio 36 - 132p6n + 121p12n
O polinômio possui dois termos quadrados 36 e 121p12n, e cujas raízes quadradas são, respectivamente, 6 e 116n. O dobro do produto
entre essas raízes é exatamente igual ao terceiro termo 132p6n.
E dessa forma o polinômio 36 - 132p6n + 121p12n é um trinômio quadrado perfeito e pode, portanto, ser fatorado.
A raiz quadrada do primeiro termo quadrado é 6, a raiz do segundo termo quadrado é 11p6n e o sinal que os une será o sinal do terceiro
termo - 132p6n, Dessa forma, teremos :
36 - 132p6n + 121p12n = ( 6 - 11p6n)2
Terceiro Caso de Fatoração : Diferença de Dois Quadrados
Já aprendemos em produtos notáveis que :
(a + b) (a - b) = a2 - b2
O que faremos agora é transformarmos a diferença algébrica a2 - b2 em sua forma fatorada (a + b) (a - b). E para tal precisamos extrair
as raízes quadradas de ambos os termos e montarmos com essas raízes a sua soma multiplicada por sua diferença.
Exemplo 06) Fatore o binômio 64x2 - 25y8
O binômio é uma diferença de dois quadrados 64x2 e 25y8, e cujas raízes quadradas são, respectivamente, 8x e 5y4.
Montando a soma (8x + 5y4) e a diferença (8x - 5y4) e as multiplicando, teremos nossa fatoração concluída. Assim :
64x2 - 25y8 = (8x + 5y4) (8x - 5y4)
Exemplo 07) Fatore 81 - 0,49k6
O binômio é uma diferença de dois quadrados 81 e 0,49k6, e cujas raízes quadradas são, respectivamente, 9 e 0,7k3.
Montando a soma (9 + 0,7k3) e a diferença (9 - 0,7k3) e as multiplicando, teremos nossa fatoração concluída. Assim :
81 - 0,49k6 = (9 + 0,7k3) (9 - 0,7k3)
Veja que interessante: Já sabemos que 49 - 25 = 24.
Vamos fazer essa diferença entre dois quadrados utilizando a fatoração, que acabamos de aprender:
49 - 25 = (7 + 5) ( 7 - 5 ) = 12 x 2 = 24 ( deu, é claro, o mesmo resultado )
Quarto Caso de Fatoração : Trinômio de Stevin
Já aprendemos em produtos notáveis que :
(a + b) (a + c) = a2 + (b + c)a + bc, que podemos escrever como : a2 + Sa + P, onde S é a soma dos termos não comuns e P o seu
produto.
O que faremos agora é transformarmos a soma algébrica a2 + Sa + P em sua forma fatorada (a + b) (a + c).
E para tal precisamos extrair a raiz quadrada do termo quadrado e descobrirmos dois número cuja soma seja S e cujo produto seja P. e
verificarmos se a soma aparece multiplica pela raiz quadrada do termo comum.
Só com alguns exemplos poderemos entender melhor esse tipo de fatoração. Vamos a eles.
Exemplo 08) Fatore o trinômio k2 + 8k + 15
Extraindo a raiz quadrada do termo quadrado k2, teremos k. Vamos descobrir agora dois números que somados sejam iguais a 8 e
multiplicados sejam iguais a 15. Esses números serão 3 e 5, já que: 3 + 5 = 8 e 3 x 5 = 15. Percebemos, também, que a soma 8 aparece
multiplicada pela raiz quadrada k de k2.
Assim : k2 + 8k + 15 = (k + 3) (k + 5)
Exemplo 09) Fatore o trinômio m4 - 6m2 + 8
Extraindo a raiz quadrada do termo quadrado m4, teremos m2. Vamos descobrir agora dois números que somados sejam iguais a - 6 e
multiplicados sejam iguais a 8. Esses números serão - 2 e - 4 , já que: - 2 + - 4 = - 6 e (- 2) x (- 4) = + 8. Percebemos, também, que a
soma - 6 aparece multiplicada pela raiz quadrada m2 de m4.
Assim : m4 - 6m2 + 8 = (m2 - 2) (m2 - 4)
Exemplo 10) Fatore o trinômio 25y6 + 20y3 - 21
Extraindo a raiz quadrada do termo quadrado 25y6, teremos 5y3. Vamos descobrir agora dois números que somados sejam iguais a + 4,
lembremos que a raiz de 9y6, está presente nesse termo, assim, 20y3 : 5y3 = 4 e multiplicados sejam iguais a - 21.
Esses números serão - 3 e + 7 , já que: - 3 + 7 = 4 e (- 3) x (+ 7) = - 21. Percebemos, como já vimos, que a soma + 4 aparece
multiplicada pela raiz quadrada 5y3 de 25y6.
Assim : 25y6 + 20y3 - 21 = (5y3 + 7) (5y3 - 3)
Exemplo 11) Fatore o trinômio 4p8 - 8p4a - 5a2
Extraindo a raiz quadrada do termo quadrado 4p8, teremos 2p4. Vamos descobrir agora dois números que somados sejam iguais a - 4a,
lembremos que a raiz de 4p8, está presente nesse termo, assim, - 8p4a : 2p4 = 4a e multiplicados sejam iguais a - 5a2.
Esses números serão - 5a e + 1a , já que: - 5a + 1a = 4a e (- 5a) x (+ a) = - 5a2. Percebemos, como já vimos, que a soma + 4a aparece
multiplicada pela raiz quadrada 2p4 de 4p8.
Assim : 4p8 - 8p4a - 5a2 = (2p4 + a) (2p4 - 5a)
Quinto Caso de Fatoração : Soma de Dois Cubos
Um binômio soma da forma x3 + y3 pode ser fatorado em um produto da forma:
x3 + y3 = (x + y) ( x2 - xy + y2)
A melhor forma para fatorarmos uma soma de dois cubos é compreendermos que um dos fatores será a soma das raízes cúbicas dos
termos cúbicos originais, e a partir dele, montarmos o outro fator que será o quadrado do primeiro menos o produto entre o primeiro e
o segundo mais ( sempre mais ) o quadrado do segundo. Só praticando entenderemos esse caso fatoração.
Exemplo 12) Fatore a soma de dois cubos 8p6 + 125
Como ambos são termos cúbicos, essa soma poderá ser fatorada.
A raiz cúbica de 8p6 é 2p2 e a raiz cúbica de 125 é 5. Assim já temos o nosso primeiro fator (2p2 + 5)
A partir dele montaremos o nosso segundo fator. O quadrado de 2p2 é 4p4 ; o produto entre 2p2 e 5 é 10p2 e o quadrado do
segundo é 52 = 25. E dessa forma, teremos:
8p6 + 125 = (2p2 + 5) ( 4p4 - 10p2 + 25)
Exemplo 13) Fatore 27x3y9 + 64z6
Como ambos são termos cúbicos, essa soma poderá ser fatorada.
A raiz cúbica de 27x3y9 é 3xy3 e a raiz cúbica de 64z6 é 4z3.
Assim já temos o nosso primeiro fator (3xy3 + 4z2)
A partir dele montaremos o nosso segundo fator. O quadrado de 3xy3 é 9x2y6 ; o produto entre 3xy3 e 4z2 é 12xy3z2 e o quadrado do
segundo é (4z2)2 = 16z4.
E dessa forma, teremos: 27x3y9 + 64z6 = (3xy3 + 4z2) (9x2y6 - 12xy3z2 + 16z4)
Sexto Caso de Fatoração : Diferença de Dois Cubos
Um binômio diferença da forma x3 - y3 pode ser fatorado em um produto da forma:
x3 - y3 = (x - y)( x2 + xy + y2)
A melhor forma para fatorarmos uma diferença de dois cubos é compreendermos que um dos fatores será a diferença das raízes
cúbicas dos termos cúbicos originais, e a partir dele, montarmos o outro fator que será o quadrado do primeiro mais o produto entre o
primeiro e o segundo mais ( sempre mais ) o quadrado do segundo. Só praticando entenderemos esse caso fatoração.
Exemplo 14) Fatore a diferença de dois cubos 216p3 - 125m6
Como ambos são termos cúbicos, essa diferença poderá ser fatorada.
A raiz cúbica de 216p3 é 6p e a raiz cúbica de 125 m6 é 5m2. Assim já temos o nosso primeiro fator (6p - 5m2)
A partir dele montaremos o nosso segundo fator. O quadrado de 6p é 36p2 ; o produto entre 6p e 5m2 é 30pm2 e o quadrado do segundo
é (5m2)2 = 25m4.
E dessa forma, teremos: 216p3 - 125m6 = (6p - 5m2) ( 36p2 + 30pm2 + 25m4)
Sétimo Caso de Fatoração : Agrupamento
Quando em um polinômio dois ou mais termos possuem um termo comum que evidenciado faz aparecer um termo comum à fatoração
dos demais termos. Só com alguns exemplos podemos compreender melhor esse caso de fatoração.
Por essa razão o deixamos como o último caso de fatoração.
Exemplo 15) Fatore o polinômio ac + ad + bc + bd (1ª resolução )
Se colocarmos, nos dois primeiros termos, o fator comum a em evidência e colocarmos, nos dois últimos termos, o fator comum b em
evidência, teremos :
ac + ad + bc + bd = a(c + d) + b( c + d). E colocando o novo fator comum (c + d) em evidência, teremos :
ac + ad + bc + bd = a(c + d) + b(c + d) = (c + d) (a + b)
Exemplo 16) Fatore o polinômio ac + ad + bc + bd (2ª resolução )
Vamos agrupar agora o primeiro e o terceiro termo e, também, o segundo e o quarto termo.
ac + ad + bc + bd = ac + bc + ad + bd
Se colocarmos, nos dois primeiros termos, o fator comum c em evidência e colocarmos, nos dois últimos termos, o fator comum d em
evidência, teremos :
ac + bc + ad + bd = c(a + b) + d(a + b)
E colocando o novo fator comum (a + b) em evidência, teremos :
ac + bc + ad + bd = c(a + b) + d(a + b) = (a + b) (c + d)
Exemplo 17) Fatore o polinômio 2am + an - 6bm - 3bn
Se colocarmos, nos dois primeiros termos, o fator comum a em evidência e colocarmos, nos dois últimos termos, o fator comum - 3b em
evidência, teremos :
2am + an - 6bm - 3bn = a(2m + n) - 3b(2m + n).
E colocando o novo fator comum (2m + n) em evidência, teremos :
2am + an - 6bm - 3bn = a(2m + n) - 3b(2m + n) = (2m + n) (a - 3b)
Exemplo 18) Fatore 3a2x - 2b2 + 2a2 - 3b2x
Reagrupando o polinômio, teremos : 3a2x - 3b2x + 2a2 - 2b2
Se colocarmos, nos dois primeiros termos, o fator comum 3x em evidência e colocarmos, nos dois últimos termos, o fator comum 2 em
evidência, teremos :
3a2x - 3b2x + 2a2 - 2b2 = 3x(a2 - b2) - 2(a2 - b2)
E colocando o novo fator comum (a2 - b2) em evidência, teremos :
3a2x - 3b2x + 2a2 - 2b2 = 3x(a2 - b2) - 2(a2 - b2) = (a2 - b2) (3x - 2)
E como o fator (a2 - b2) é fatorável e igual a (a + b) (a - b), teremos, finalmente :
3a2x - 3b2x + 2a2 - 2b2 = 3x(a2 - b2) - 2(a2 - b2) = (a2 - b2) (3x - 2) = (a + b) (a - b) (3x - 2)
Com isso, apresentamos os mais importantes casos de fatoração. Alguns exercícios resolvidos e um pouco mais complexos,
nos ajudarão no entendimento desse assunto da Álgebra, que é um dos que mais dificuldades apresenta aos alunos.
Exercícios Resolvidos de Fatoração Algébrica
Exemplo 19) Fatore c2 - 2bc - a2 + b2
Reagrupando o polinômio, teremos : b2 - 2bc + c2 - a2 = (b2 - 2bc + c2) - a2
O trinômio b2 - 2bc + c2 pode ser fatorado como : (b - c)2
E dessa forma, teremos a diferença de dois quadrados (b - c)2 - a2, e finalmente, teremos :
(b - c)2 - a2 = (b - c + a) (b - c - a)
Exemplo 20) Fatore: 5m8 + 10m4 - 15
Percebemos que o fator 5 pode ser evidenciado, Assim:
5m8 + 10m4 - 15 = 5(m8 + 2m4 - 3)
O trinômio m8 + 2m4 - 3 não é um trinômio quadrado perfeito, mas poderá ser um trinômio de Stevin.
E realmente o é, pois os números 3 e -1, têm por soma 2 e por produto - 3, e a soma aparece multiplicada pela raiz quadrada m4 de m8.
Dessa forma, teremos : 5m8 + 10m4 - 15 = 5(m8 + 2m4 - 3) = 5(m4 + 3) (m4 - 1)
E como (m4 - 1) = (m2 + 1) (m2 - 1) , e como (m2 - 1) (m + 1)(m - 1) teremos : 5m8 + 10m4 - 15 = 5(m4 + 3)(m2 + 1)(m + 1)(m - 1)
Exemplo 21) Fatore: (x - y)2 + 2(y - x) - 24
Antes de mais nada, lembremos que (x - y)2 = (y - x)2 ( verifique se isso é verdade )
Com isso podemos escrever a expressão dada como : (y - x)2 + 2(y - x) - 24
Para facilitar o reconhecimento do caso de fatoração, chamemos o binômio (y - x) de A, então :
(y - x)2 + 2(y - x) - 24 = A2 + 2A - 24
O trinômio não é quadrado perfeito, mas parece ser de Stevin.
Verificando, percebemos que os números - 4 e + 6 têm por soma + 2 e por produto - 24 e a soma + 2 aparece multiplicada pela raiz
quadrada A de A2.
E assim : A2 + 2A - 24 = (A + 6) (A - 4) e como A = y - x, finalmente teremos: (x - y)2 + 2(y - x) - 24 = (y - x + 6) (y - x - 4)
Exemplo 22) Fatore x6 - y6
1ª Resolução: Considerando uma diferença de dois cubos
Como ambos são termos cúbicos, essa diferença poderá ser fatorada.
A raiz cúbica de x6 é x2 e a raiz cúbica de y6 é y2. Assim já temos o nosso primeiro fator x2 - y2
A partir dele montaremos o nosso segundo fator. O quadrado de x2 é x4 ; o produto entre x2 e y2 é x2y2 e o quadrado do
segundo é y2 é y4.
E dessa forma, teremos:
x6 - y6 = (x2 - y2) ( x4 + x2y2 + y4). Como a diferença de quadrados (x2 - y2) ainda pode ser fatorado, teremos :
x6 - y6 = (x + y) (x - y) ( x4 + x2y2 + y4).
Se escrevermos o trinômio ( x4 + x2y2 + y4) de uma outra forma, perceberemos que ele também poderá ser fatorado. Vejamos :
x4 + x2y2 + y4 = x4 + 2x2y2 + y4 - x2y2 = (x2 + y2)2 - x2y2, que é uma diferença de dois quadrados.
Assim : (x2 + y2)2 - x2y2 = ( x2 + y2 + xy) ( x2 + y2 - xy) = ( x2 - xy + y2) ( x2 + xy + y2). E finalmente :
x6 - y6 = (x + y) (x - y) ( x2 - xy + y2) ( x2 + xy + y2)
2ª Resolução: Considerando uma diferença de dois quadrados. Como ambos são quadrados, temos uma diferença de dois quadrados.
A raiz quadrada de x6 é x3 e a raiz quadrada de y6 é y3.
Assim já temos o nosso primeiro fator (x3 + y3) e o segundo fator (x3 - y3).
Assim, teremos : x6 - y6 = (x3 + y3) (x3 - y3) .
Como a soma e a diferença de dois cubos (x3 + y3) e (x3 - y3) ainda podem ser fatorados, teremos :
x6 - y6 = (x3 + y3) (x3 - y3) = (x + y) ( x2 - xy + y2) (x - y) ( x2 + xy + y2) , ou ainda :
x6 - y6 = (x + y) (x - y) ( x2 - xy + y2) ( x2 + xy + y2)
OBSERVAÇÃO MUITO IMPORTANTE
Sempre que fatoramos uma expressão algébrica ou quando efetuamos um produto notável devemos utilizar o sinal de identidade
que é uma ampliação do conceito de igualdade.
Vamos entender melhor essa diferenciação:
Quando afirmamos que 3x + 4 = 19, sabemos que apenas o valor de x = 5 tornará verdadeira essa sentença.
Nesse caso utilizaremos o sinal de igualdade.
Quando afirmamos que 2(x + 3) = 2x + 6, percebemos que qualquer valor de x, torna essa sentença verdadeira.
Nesse caso devemos utilizar o sinal de identidade .
www.matematicafacil.com
Fatoração de Polinômios
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
http://accbarrosogestar.blogspot.com.br
Fatoração de Polinômios
Por Marcos Noé
Polinômios
As fatorações mais conhecidas são: fator comum em evidência, agrupamento, diferença entre dois quadrados, trinômio quadrado perfeito e trinômio soma e produto.
Fator comum em evidência
Nesse modelo de fatoração temos que determinar o elemento comum aos termos que formam o polinômio. Observe:
No polinômio x² + 2x, temos que a variável x é comum aos dois termos. Ela será o termo em evidência, a qual dividirá todos os termos do polinômio original.
x² + 2x → x * (x + 2)
x² : x = x
2x : x = 2
Veja mais exemplos de fatoração por evidência:
4x³ – 2x² → 2x² * (2x – 1)
4x³ : 2x² = 2x
2x : 2x = 1
16x² + 8 → 8 * (2x² + 1)
16x² : 8 = 2x²
8 : 8 = 1
Fatoração por Agrupamento
Na fatoração por agrupamento, utilizamos inicialmente a fatoração por evidência e logo em seguida agrupamos os termos sob certas condições também de evidenciação. Observe:
2yx – x – 6y + 3, aplicar evidência entre 2yx e –x e entre –6y e 3.
2yx – x → x * (2y – 1)
–6y + 3 → –3 * (2y – 1)
2yx – x – 6y + 3 → x * (2y – 1) – 3 * (2y – 1) → (x – 3) * (2y – 1)
Observe mais exemplos:
bx – 2b + x – 2 → bx + x – 2b – 2 → x * (b + 1) – 2 * (b + 1) → (x – 2) * (b + 1)
10x² + 15xy + 4x + 6y → 10x² + 4x + 15xy + 6y → 2x * (5x + 2) + 3y * (5x + 2) → (2x + 3y) * ( 5x + 2)
Diferença entre dois quadrados
Nessa fatoração aplicaremos a raiz quadrada entre os elementos. O valor resultante das raízes formará uma multiplicação entre binômios no mesmo modelo do notável produto da soma pela diferença. Veja:
4x² – 16 → (2x + 4) * (2x – 4)
√4x² = 2x
√16 = 4
25x² – 100 → (5x + 10) * (5x – 10)
√25x² = 5x
√100 = 10
81x4 – 144 → (9x² + 12) * (9x² – 12)
√81x4 = 9x²
√144 = 12
400x² – 49 → (20x + 7) * (20x – 7)
√400x² = 20x
√49 = 7
Trinômio quadrado perfeito
Determinaremos o produto notável responsável pela formação do trinômio x² + 2xy + y² ou x² – 2xy + y². Observe:
x² + 18x + 81 → (x + 9)²
√x² = x
√81 = 9
(x + 9)² = (x + 9) * (x + 9) = x² + 9x + 9x + 81 = x² + 18x + 81
4x² – 48x + 144 → (2x – 12)²
√4x² = 2x
√144 = 12
(2x + 12)² = (2x + 12) * (2x + 12) = 4x² + 24x + 24x + 144 = 4x² + 48x + 144
Trinômio Soma e Produto
São as fatorações envolvendo trinômios do tipo x² + Sx + P, que podem ser fatorados e escritos da seguinte forma (x + a) * (x + b). Nessa situação temos que Soma = a + b e Produto = a * b. Observe:
x² + 10x + 16 → (x + 8) * (x + 2)
Soma = 10
Produto = 16
Os números são 8 e 2, pois:
8 + 2 = 10
8 * 2 = 16
x² – 13x + 42 → (x – 6) * (x – 7)
Soma = –13
Produto = 42
Os números são –6 e –7, pois:
– 6 – 7 = – 13
(–6) * (–7) = 42
x² + 3x – 10 → (x – 2) * (x + 5)
Soma = 3
Produto = –10
Os números são 3 e –10, pois:
– 2 + 5 = 3
(–2) * 5 = – 10
x² – 2x – 63 → (x – 9) * (x + 7)
Soma = –2
Produto = – 63
Os números são –9 e 7, pois:
– 9 + 7 = – 2
(–9) * 7 = – 63
Vícios de Linguagem

Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
1. Barbarismo: Grifo ou pronúncia de uma palavra em desacordo com a norma culta.
“Gratuíto” (em vez de gratuito)
“Rítmo” (em vez de ritmo)
2. Solecismo: Desvio da norma em relação à sintaxe.
“Fazem dois anos que não nos vemos” (em vez de faz)
3. Ambiguidade ou Anfibologia: Deixar a frase com mais de um sentido.
“O menino viu o incêndio da escola”
4. Cacófato: Mau som produzido pela junção de palavras.
“Beijou na boca dela”.
“Eu vi ela”. (Eu viela?)
"Eu amo ela" (Eu a moela?)
“Não tenho pretensão acerca dela”.
(Não tenho pretensão a ser cadela?)
“Vou-me já porque já está pingando”.
(Vou mijar porque já está pingando?)
"Tenho culpa eu" (Tem c... pá eu?!)
5. Pleonasmo Vicioso: repetição desnecessária de palavras para expressar uma idéia.
“Subir pra cima”
“Entra pra dentro, menino!”
6. Neologismo: criação desnecessária de palavras novas.
“O ministro se considerava imexível”
7. Eco: Repetição de um som numa seqüência de palavras.
“A decisão da eleição não causou comoção na população.”
8. Arcaísmo: Utilização de palavras que já caíram em desuso.
“Vossa Mercê vai pescar”
www.algosobre.com.br
Genética - os seguidores de Mendel Dos cromossomos ao DNA
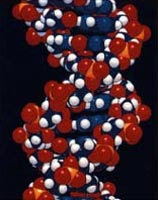
A estrutura molecular do DNA
Walter Sutton, um estudante de graduação no laboratório da Universidade de Columbia, nos EUA, foi o primeiro a declarar, em 1902, que os cromossomos obedecem às leis de Mendel. Ele se especializou no estudo de cromossomos de gafanhotos, dando início às pesquisas citológicas que contribuiriam para a elaboração da teoria cromossômica da hereditariedade.
Em seu trabalho, Sutton concluiu que, durante o processo de meiose, no qual são produzidos óvulos e espermatozóides, cada gameta recebe apenas um cromossomo de cada tipo. Nas outras partes do corpo, as células possuem dois cromossomos de cada tipo, herdados de cada genitor. O padrão de segregação dos cromossomos durante a meiose corresponde aos padrões de segregação propostos por Mendel.
Naquele mesmo ano, um citologista alemão, T. Boveri, reconheceu que os cromossomos individuais são diferentes uns dos outros, mas não fez nenhuma conexão com os princípios mendelianos. No entanto, o supervisor de Sutton, E. B. Wilson, ofereceu co-autoria a Boveri pela proposição da teoria cromossômica da hereditariedade.
Um ano mais tarde, Sutton publicou um trabalho intitulado "Os cromossomos na hereditariedade", no qual desenvolve com maiores detalhes sua hipótese. De acordo com alguns pesquisadores, com este trabalho de Sutton se inicia o estudo da citogenética.
Apesar do nascimento de uma disciplina - a citogenética - que une os estudos da célula (citologia), dos genes e de sua transmissão às gerações seguintes (genética) ter ocorrido no ano de 1903, a palavra gene só foi criada em 1909, pelo botânico dinamarquês Wilhelm Johannsen, quando ele descreveu os fatores da hereditariedade nas experiências de Mendel.
No que se refere ao termo genética, ele foi usado quatro anos antes pelo geneticista William Bateson em uma carta, mas só passou a ser utilizado pelos cientistas após a criação do termo gene por Johannsen. O termo gene vem da palavra grega genos, que significa nascimento.
Morgan, Beadle e Tatum
Depois dos gafanhotos, as moscas se tornaram um organismo modelo nos estudos da hereditariedade. Estudando as moscas Drosophila melanogaster, o pesquisador Thomas Hunt Morgan e seus colaboradores da Universidade de Columbia mostraram, no ano de 1911, que os genes estão localizados nos cromossomos e são as unidades da hereditariedade. Eles confirmaram a teoria cromossômica da hereditariedade e, por isso, Thomas Hunt Morgan recebeu, em 1933, o Prêmio Nobel de Fisiologia ou Medicina.
No ano de 1941, os cientistas George Beadle e Edward Tatum mostraram, por meio de experimentos com o fungo vermelho do pão, Neurospora crassa, que os genes agem regulando eventos químicos distintos. Eles concluíram que a função de um gene é dar instruções para a formação de uma enzima particular, que regula um evento químico.
Beadle e Tatum propuseram que, em geral, um gene codifica para a produção de uma enzima. A hipótese de Beadle e Tatum ficou conhecida como "um gene, uma enzima". Posteriormente, o nome da hipótese foi modificado para "um gene, um polipeptídeo", já que algumas proteínas são compostas por diferentes cadeias de polipeptídeos, codificados por genes separados.
O DNA revelado pelos raios X
Os cientistas interessados em ampliar os estudos de genética iniciaram suas pesquisas pelo nível celular, com os cromossomos, e, pouco a pouco, foram se aprofundando, até chegar ao nível molecular.
O DNA havia sido descoberto, no ano de 1868, pelo biólogo suíço Friedrich Miescher, mas permaneceu sem muita importância por cerca de 70 anos. Em 1943, o cientista britânico William Astbury extraiu o DNA de células, mergulhou uma agulha na solução viscosa de DNA e puxou um filamento contendo muitas moléculas alinhadas, quase que em paralelo, umas com as outras. Ele obteve, então, um padrão de difração de raios X para visualizar a molécula de DNA.
Os padrões de difração de raios X de moléculas cristalizadas podem revelar suas estruturas com precisão atômica. Esta técnica revelou o DNA como uma estrutura regular e periódica. Astbury sugeriu que as bases de nucleotídeo do DNA estavam empilhadas umas sobre as outras como "uma pilha de moedas".
Em 1952, Alfred Hershey e Martha Chase mostraram, com o auxílio de marcadores radioativos, que, quando um vírus infecta uma célula hospedeira (a bactéria Escherichia coli), para nela se reproduzir, é o seu DNA que invade a bactéria e não a sua capa protéica. Este experimento corroborou a hipótese feita pelos cientistas Avery, McLeod e McCarty no ano de 1944, de que o DNA é a molécula responsável pela hereditariedade. O experimento de Alfred Hershey e Martha Chase ofereceu suporte para a idéia de que os genes são feitos de DNA.
Muito já se sabia sobre o DNA no ano de 1953:
# que o DNA é composto de nucleotídeos formados por três partes: um grupo fosfato, um açúcar com cinco átomos de carbono (pentose) e bases nitrogenadas (adenina, citosina, guanina e timina);
# que no DNA de qualquer tipo de célula a quantidade de adenina é, aproximadamente, a mesma de timina, enquanto que a quantidade de citosina é aproximadamente a mesma de guanina. Isto foi demonstrado por Erwin Chargaff, em 1949;
# e que o DNA possui grande simetria e consistência em sua estrutura.
A estrutura molecular do DNA
Dois pesquisadores do laboratório Cavendish, na Inglaterra, se dedicaram a obter mais informações sobre a estrutura química do DNA. O físico Francis Crick e o zoólogo James Watson se apressaram em desvendar a estrutura do DNA antes de qualquer pessoa. Eles competiam com o químico Linus Pauling.
Enquanto Watson e Crick trabalhavam em seu modelo, Pauling publicou um trabalho sugerindo uma estrutura de tripla hélice para o DNA. O modelo de Pauling foi criticado por conter imperfeições químicas. Ao ler o trabalho de Pauling, Watson convenceu seus colegas de que tinha a interpretação correta. Um dos colegas, Maurice Wilkins, mostrou a Watson as imagens mais recentes de difração de raios X do DNA. Ao ver as imagens, Watson teve certeza de que sua idéia estava correta e começou a construir, junto com Crick, o novo modelo da estrutura do DNA.
O modelo de Watson e Crick revelou as seguintes propriedades:
# o DNA é uma dupla hélice, com o açúcar e o fosfato dos nucleotídeos formando os dois filamentos da hélice - e as bases nitrogenadas apontando para o interior da hélice e empilhando-se umas sobre as outras;
# as bases nitrogenadas usam pontes de hidrogênio para parearem especificamente, com uma adenina sempre se opondo a uma timina, e uma citosina sempre se opondo a uma guanina;
# os dois filamentos da dupla hélice correm em direções opostas.
Em 1962, Watson, Crick e Wilkins receberam o prêmio Nobel de Fisiologia ou Medicina pela descoberta da estrutura molecular do DNA.
Sono O que acontece enquanto dormimos?

Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
O sono, na visão do pintor surrealista Salvador Dalì
O sono é uma atividade fisiológica essencial à nossa saúde e à nossa sobrevivência. É durante o sono que ocorrem diversos processos metabólicos, através dos quais o corpo se recupera e se desenvolve. Pesquisas demonstram que repousar, sem dormir, não apresenta os mesmos resultados de uma boa noite de sono.
A privação do sono leva, entre outras coisas, a uma queda na atenção, dificuldades em aprender novas tarefas motoras, alterações emocionais e dificuldades de memorização.
O que é o sono?
O ciclo de sono e vigília se repete a cada 24 horas, ou seja, apresenta o que chamamos de ritmo circadiano. Estudos demonstram que esse ciclo se mantém mesmo em condições nas quais não se possui acesso à passagem do tempo. Pessoas mantidas em salas escuras continuaram dormindo e acordando aproximadamente a cada 24 horas.
Isso sugere que o controle do sono não depende apenas de fatores externos, e mas também de mecanismos internos (endógenos) do organismo. Esses mecanismos são chamados de relógios biológicos e são capazes de controlar os ritmos biológicos mesmo na ausência de estímulos ambientais.
Fisiologicamente, o sono é descrito como o estado no qual o indivíduo não responde facilmente a estímulos sensoriais, a atividade motora fica reduzida e há uma perda temporária da consciência. Já a vigília corresponde ao estado no qual o indivíduo responde facilmente a estímulos e apresenta alta atividade motora e cognitiva.
Fases do sono
O sono não é um fenômeno homogêneo. Ele ocorre de forma cíclica e cada ciclo apresenta vários estágios, alternando fases de sono profundo e leve. Em média, cada ciclo dura entre 60 e 90 minutos e é dividido nos seguintes estágios:
Estágio 1: é a fase inicial do sono, ou seja, a transição entre o estado de vigília e o sono. Pode durar de alguns segundos a até cerca de 5 minutos. É caracterizado pelo sono leve, do qual somos facilmente despertados. O estado de consciência é baixo e a atenção, reduzida. Nessa fase, o indivíduo pode ouvir e falar, mas, provavelmente, não irá se lembrar depois que acordar. Corresponde a cerca de 5% do tempo total de sono e pode ocorrer também durante a mudança de estágios.
Estágio 2: ainda é uma fase de sono leve, mas não tanto como no estágio 1. Dura de 10 a 20 minutos.
Estágio 3: é o início do sono profundo. A atividade cerebral se torna mais lenta e o processo de recuperação fisiológica do organismo se inicia. Dura de alguns segundos até cerca de 5 minutos.
Estágio 4: sono profundo. Nesta fase diminuem a freqüência cardíaca, a respiração e a temperatura corporal. É neste estágio que ocorre a produção de hormônios. Dura cerca de 20 minutos.
Sono REM: também conhecido como estágio 5 ou sono paradoxal. No sono REM, os olhos se mexem rapidamente por baixo das pálpebras fechadas, porém o restante da musculatura do corpo permanece totalmente relaxada. O nome REM vem da sigla em inglês para movimentos rápidos dos olhos (rapid eyes movements). Nesta fase, embora a pessoa esteja dormindo profundamente, as ondas cerebrais possuem um padrão de atividade similar àquele da vigília, daí o nome sono paradoxal. Este estágio dura de 15 a 20 minutos e é nele que ocorrem os sonhos.
Quanto tempo devemos dormir?
Em média, adultos devem dormir entre 7 e 9 horas diárias. Este número varia conforme a idade, as atividades realizadas e outras características individuais. Crianças precisam dormir um número maior de horas.
Um bebê recém-nascido dorme cerca de 18 horas; com 1 ano de idade, entre 13 e 14 horas. Ou seja, o número de horas tende a diminuir com o aumento da idade, até atingir uma média de 8 horas diárias.
Agora que já sabemos as funções e as características de uma boa noite de sono vamos ver como despertamos. Existem duas maneiras de acordar. Uma delas é ser despertado por estímulos externos intensos, como sons, sensações táteis ou luz intensa. Esses estímulos tiram de sincronia os impulsos nervosos do córtex cerebral e nos despertam. A outra forma é despertar espontaneamente e isso geralmente ocorre após o término de um ciclo completo de sono.
Distúrbios do sono
Os distúrbios do sono são alterações que afetam o início ou todo o sono e podem ter origem emocional ou fisiológica. Alguns destes distúrbios são a insônia, a narcolepsia, a apnéia do sono e o terror noturno.
A insônia é caracterizada pela dificuldade em pegar no sono ou por manter o sono por um período contínuo, levando à fadiga, falta de atenção e indisposição durante o dia. Pode ter origem emocional, como o estresse, ou fisiológica, como distúrbios hormonais ou neurológicos.
A narcolepsia é um distúrbio pouco comum, marcado por episódios de sono súbito e incontrolável ao longo do dia, mesmo em situações inesperadas, como quando o indivíduo está de pé ou conversando com alguém. Este sono possui curta duração e, geralmente, não ultrapassa 30 minutos. As causas da doença ainda não foram descobertas, mas, como costuma afetar vários membros de uma mesma família, acredita-se que exista uma predisposição genética.
A apnéia do sono é caracterizada por paradas curtas e repetitivas da respiração durante o sono. Costuma-se classificar este distúrbio em dois tipos, dependendo da origem. Quando a apnéia é causada por disfunção no controle neurológico da respiração, é chamada de apnéia do sono central. Quando é provocada por obstrução das vias aéreas, é chamada de apnéia do sono obstrutiva.
O terror noturno é considerado uma manifestação severa do sonambulismo. Geralmente, o portador do distúrbio se levanta no meio do sono profundo, muito agitado, com a respiração e os batimentos cardíacos acelerados e, por vezes, gritando como se estivesse aterrorizado. Aparentemente, estes episódios não estão relacionados a pesadelos ou sonho perturbadores. Ao acordar, a pessoa geralmente não se lembra de nada.
É importante procurar ajuda médica ao sentir dificuldade para dormir ou alguma outra disfunção durante o sono, pois somente um especialista poderá fazer o diagnóstico correto e prescrever o tratamento adequado.
Alice Dantas Brites é professora de biologia.
Assinar:
Postagens (Atom)