O Problema das Oito Caixas e uma P.G. -Tudo a Ver!
Esse texto foi retirado da obra de Malba Tahan e chama-se "O Problema das Oito Caixas" que é um dos contos do matemático e escritor Ali Iezid Izz-Edim Ibn Salim Hank Malba Tahan ou simplesmente "Malba Tahan" que é o pseudônimo do professor de Matemática Júlio César de Mello e Souza, nascido no Rio de Janeiro, em 1895, e falecido no ano de 1974, no Recife, aos 79 anos. Malba Tahan escreveu mais de uma centena de livros sobre Matemática Recreativa, Didática da Matemática, História da Matemática e Literatura Infanto-juvenil. O texto é recomendado por muitos especialistas em educação para fazer parte dos conteúdos envolvendo a interdisciplinaridade e sobretudo para assessoramento no tópico de progressão geométrica do ensino de matemática em nível médio.
(conto do matemático: Malba Tahan)
Segundo uma lenda muito antiga, o célebre Califa Al Motacém Billah, rei dos árabes, chamou certa manhã o astucioso Sabag, seu vizir-tesoureiro, e disse-lhe em tom grave, como se ditasse uma sentença irrevogável:
— Dentro de poucas horas, meu caro vizir, receberei a visita do jovem Beremiz Samir, apelidado “o homem que calculava”. Não ignoras, certamente, que o talentoso Beremiz tem deslumbrado esta nossa gloriosa Bagdá com inequívocas demonstrações de seu incomparável engenho e de sua agudíssima inteligência. Os enigmas mais intrincados, os cálculos mais difíceis são, pelo exímio matemático, explicados e resolvidos em rápidos momentos.
É meu desejo presentear o ilustre Beremiz com avultada quantia. Gostaria, entretanto, de experimentar também a tão elogiada argúcia do calculista, propondo-lhe durante a nossa entrevista um problema que seja relacionado, de certo modo, com o prêmio que lhe darei em moedas de ouro. Um problema que deixasse o nosso visitante encantado, é verdade, mas também perplexo e confuso.
O vizir Sabag não era homem que se deixasse entibiar diante dos caprichos e fantasias do poderoso emir. Depois de ouvir, cabisbaixo e pensativo, as palavras do rei, ergueu o rosto bronzeado, fitou serenamente o glorioso califa, e assim falou:
— Escuto e obedeço, ó Príncipe dos Crentes! Pelo tom de vossas palavras, adivinho perfeitamente o rumo seguido pela caravana de vossas intenções. É vosso desejo premiar um sábio geômetra com valiosa quantia. Ressalta, dessa intenção, a generosidade sem par de vosso coração. Quereis, entretanto, que este prêmio seja exorado com um problema original e inédito, capaz de surpreender o mais engenhoso dos matemáticos e de encantar o mais delicado dos filósofos. Essa lembrança põe em relevo a elegância de vossas atitudes, pois o visitante, ao ser arguido diante da corte, poderá mais uma vez demonstrar a pujança de seu engenho e o poderio de sua cultura.
Proferidas tais palavras, retirou-se o vizir para a sua sala de trabalho. Decorrido algum tempo, voltou à presença do rei, precedido de dois escravos núbios que conduziam pesada bandeja de prata. Repousavam sobre a bandeja oito caixas de madeira, todas do mesmo tamanho, numeradas de um até oito.
Não pequeno foi o espanto do califa de Bagdá ao ver aquele singular aparato. Qual seria a razão de ser daquelas caixas numeradas de um até oito? Que mistério, no domínio das contas e dos cálculos, poderiam elas envolver? Xeiques e nobres, que se achavam ao lado do rei, entreolhavam-se espantados.
Cabia ao honrado Sabag, ministro da corte, explicar o porquê daquela estranha preparação. Ouçamos, pois, o relato feito pelo digno vizir:
— Cada uma dessas caixas contém certo número de moedas. O total contido nas caixas é o prêmio que será oferecido ao calculista. As caixas, como podeis observar, estão numeradas de um até oito, e dispostas segundo o número de moedas que cada uma contém. Para esse arranjo das caixas, adotei a ordem crescente. Assim, a caixa designada pelo número 1 encerra o menor número de moedas; vem depois a que é indicada pelo número 2; a seguir aparece a de número 3, e assim por diante até a última, que encerra o maior número de moedas. Para evitar qualquer dúvida, direi desde logo que não é possível encontrar duas caixas com o mesmo número de moedas.
O califa, seriamente intrigado, interpelou o vizir:
— Não percebo, ó eloquente Sabag, que problema seria possível formular com esses dinares distribuídos por oito caixinhas. Por Allah! Não percebo!
O vizir Sabag, quando moço, fora professor primário e havia aprendido, diante das classes, a ensinar os iletrados, a esclarecer as dúvidas dos menos atilados e dirimir as questões sugeridas pelos mais espertos.
Firmemente resolvido a elucidar o glorioso soberano, o velho mestre-escola assim falou:
— Cumpre-me dizer, ó Rei do Tempo, que os dinares não foram distribuídos ao acaso pelas oito caixas. Cada caixa encerra certo número de moedas. São ao todo, portanto, oito quantias em dinares. Com as quantias distribuídas pelas oito caixas, podemos fazer qualquer pagamento, desde um dinar até o número total contido nas oito caixas, sem precisar abrir nenhuma caixa ou tocar em moeda alguma. Basta separar, da coleção que se acha sobre a bandeja, uma, duas, três, quatro ou mais caixas, e será obtido o total desejado.
— Iallah! É curioso! — comentou maravilhado o emir. — Segundo posso inferir de tua explicação, o arranjo dos dinares, distribuídos pelas oito caixas, permite que se possa retirar do total a quantia que se quiser, sem violar nenhuma das caixas, sem remover moeda alguma?
— Isso mesmo! — confirmou pressuroso o vizir. — Digamos que fosse vosso desejo retirar, por exemplo, do total a quantia de 212 dinares. Nada mais simples. No grupo das oito caixas há algumas cujas porções nelas contidas perfazem a soma de 212. Consistirá a dificuldade do problema, para cada caso, em determinar as caixas que devem ser separadas, a fim de que se obtenha uma determinada quantia, pois o que se fez para 212 poder-se-á fazer para 200, 49, 157, ou qualquer número inteiro até o total de moedas.
Feita breve pausa, a fim de permitir que o rei pudesse fixar ideias e refletir sobre o caso, o inteligente vizir rematou:
— Eis, ó Comendador dos Crentes, em resumo, o problema que poderia ser proposto, diante da corte, ao genial calculista: “Sabendo que estas caixas, numeradas de um até oito, contêm dinares em números que não se repetem; sabendo-se também que é possível efetuar qualquer pagamento até o número total de moedas, sem abrir nenhuma caixa, pergunta-se:
1º - Quantas moedas contém, respectivamente, cada uma das caixas?
2º - Como determinar, por meio do raciocínio, matematicamente certo, a quantia contida em cada uma?
3º - Qual o número total de moedas?
4º - Será possível resolver o mesmo problema distribuindo-se as moedas por um número menor de caixas?”
O divã do califado, isto é, o salão real das audiências, achava-se repleto de nobres e convidados quando, pelo soar surdo e solene do gongo, foi anunciada a visita de Beremiz Samir, “o homem que calculava”. No centro do suntuoso recinto, sobre luxuoso tapete, foi colocada a bandeja com as oito caixas que iriam servir de base para o problema.
Al-Motacém Billah, Príncipe dos Crentes, que se achava em seu trono de ouro e púrpura, rodeado de seus vizires e cádis, dirigiu ao matemático amistosa saudação:
— Sê bem-vindo, ó Beremiz! Sê bem-vindo sob a inspiração de Allah! Que a tua presença neste divã seja motivo de júbilo para todos os nossos amigos, e que de tuas palavras possamos colher as tâmaras deliciosas da sabedoria que eleva as almas e purifica os corações.
Decorreu um momento de impressionante silêncio. Competia ao visitante agradecer aquela honrosa saudação. Inclinando-se Beremiz diante do rei, assim falou:
— Allah badique, ia Sidi! — Deus vos conduza, ó Chefe! Admiro, estimo e exalto aqueles que governam com justiça, bondade e sabedoria. É esse o vosso caso, ó Emir dos Árabes, e todos os vossos súditos proclamam essa verdade. A vossa justiça assegura o poderio do Estado; a vossa bondade cria preciosas dedicações; e a vossa sabedoria fortalece e perpetua a confiança do povo. Ai daqueles cujos governantes são sábios, mas regem a vida pela injustiça das ações que praticam! Ai daqueles cujos chefes e dirigentes são justos, mas desconhecem a bondade! E Allah, o Clemente, se compadeça daqueles que se acham sob o jugo de homens ignorantes, pérfidos e iníquos.
— As tuas palavras, ó calculista — respondeu o rei mansamente — são para mim como brincos de ouro e rubis. Servem-me de estímulo e enchem-me de orgulho. Vou, mais uma vez, abusar de tua gentileza. Será um encanto, não só para mim, como para todos os nobres, vizires e xeiques que aqui se acham ouvir a tua palavra, a tua doutíssima opinião, sempre original e brilhante, sobre um problema aritmético que parece desafiar o engenho dos mais insignes matemáticos. Esse problema, formulado pelo vizir Sabag, poderia ser enunciado nos seguintes termos:
“Sobre aquela bandeja estão oito caixas. Cada caixa contém certo número de moedas, e não há duas caixas com o mesmo número de moedas. Afirma o vizir Sabag que a distribuição de moedas pelas oito caixas foi feita de modo a permitir que se possa do total, destacar qualquer quantia, desde um dinar, sem abrir nenhuma caixa, isto é, sem tocar nas moedas. Resta agora determinar quantas moedas contém cada caixa e qual o total de moedas. Para facilitar a exposição, as caixas estão numeradas de um até oito, segundo a ordem crescente das quantias que encerram”.
E o califa rematou, depois de breve pausa:
— Como orientarias, ó calculista, a solução desse engenhoso problema?
Beremiz Samir, “o homem que calculava”, como bom súdito, não se fez de rogado. Cruzou lentamente os braços, baixou o rosto e pôs-se a meditar. Depois de coordenar as ideias, iniciou a preleção sobre o caso, nos seguintes termos:
— Em nome de Allah, Clemente e Misericordioso! Esse problema é, realmente, um dos mais interessantes que tenho ouvido, e a sua solução, por ser simples e suave, põe em relevo a beleza e a simplicidade sem par da Matemática. Vejamos. A distribuição dos dinares pelas oito caixas foi feita de modo a permitir que separemos uma quantia qualquer, a partir de um dinar, destacando-se da coleção uma, duas, três ou mais caixas. Resta determinar o conteúdo de cada caixa. É evidente que a primeira caixa deve conter um dinar, pois do contrário não poderíamos destacar a unidade do total. Eis a conclusão algemada pela evidência: a caixa designada pelo número 1 contém um dinar.
A segunda caixa deverá conter, forçosamente, dois dinares, pois a quantia de um dinar não pode ser repetida, e se a segunda caixa tivesse três, quatro ou mais dinares não seria possível separar dois dinares do total. Conclusão: já conhecemos os conteúdos respectivos das duas primeiras caixas. Com auxílio dessas duas caixas podemos obter um, dois ou três dinares.
Passemos agora a terceira caixa. Quanto deveria conter? A resposta impõe-se imediatamente: quatro dinares. Com efeito, se a terceira caixa encerrasse mais de quatro dinares, não seria possível, conservando intactas as caixas, separar quatro dinares do total. Para as três primeiras, temos, portanto:
1ª caixa: 1 dinar;
2ª caixa: 2 dinares;
3ª caixa: 4 dinares.
Com auxílio dessas três caixas, podemos formar todas as quantias desde um até sete dinares. Sete representaria o total das três primeiras caixas, isto é, um mais dois mais quatro.
Repetindo o mesmo raciocínio, somos levados a afirmar que a caixa seguinte, isto é, a quarta, deverá conter oito dinares. A inclusão desta caixa com oito dinares permitirá separar do total todas as quantias desde um até quinze. O quinze é formado pelo conteúdo das quatro primeiras caixas.
E a quinta caixa? Não oferece o cálculo de seu conteúdo a menor dificuldade. Uma vez demonstrado que as quatro primeiras caixas totalizam quinze, é evidente que a quinta caixa deverá encerrar dezesseis dinares. A inclusão da quinta caixa ao grupo das quatro primeiras permite que formemos qualquer número desde um até trinta e um, inclusive. O total trinta e um é obtido pela soma das cinco primeiras.
Neste ponto fez o calculista uma pausa rapidíssima, e logo prosseguiu:
— Vejamos, pelo encadeamento natural de nosso raciocínio, se é possível descobrir uma lei, ou regra, que permita calcular os conteúdos respectivos das outras caixas restantes. Para isso convém recapitular:
1ª caixa: 1 moeda;
2ª caixa: 2 moedas;
3ª caixa: 4 moedas;
4ª caixa: 8 moedas;
5ª caixa: 16 moedas.
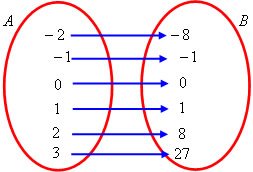
Observemos que cada caixa, a partir da segunda, contém sempre o dobro do número de moedas da caixa precedente. Dizem os matemáticos que os números 1, 2, 4, 8 e 16 formam uma progressão geométrica crescente, cuja razão é dois — um sistema binário, portanto. Dada à natureza do problema, é fácil provar que se mantém a mesma progressão fixando os conteúdos das quatro caixas seguintes. Temos então:
6ª caixa: 32 moedas;
7ª caixa: 64 moedas;
8ª caixa: 128 moedas;
E o total de moedas em todas as caixas, portanto, são 255.
— Uassalã!
Matéria Revisada, e Adaptado de Malba Tahan, O homem que calculava – Conquista, Rio, 1965.
Tem tudo a ver, pois este é o sistema binário, que é a base de funcionamento dos computadores. Bit é a menor informação usada, correspondendo ao conteúdo de uma caixa, qualquer delas; byte é a informação (número) obtida com uma ou mais caixas escolhidas dentre essas oito. O sistema de oito bits (ou oito caixas, conforme a descrição) permite computar de 0 até 255. Os dez algarismos do sistema decimal ocupam apenas dez possibilidades, e as 245 restantes são usadas pelos analistas e programadores para corresponder a letras, sinais gráficos, comandos, etc.
fonte:recordandomatematica.blogspot.com.br