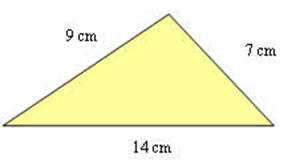
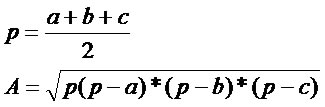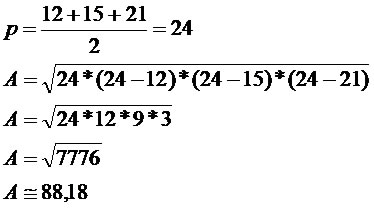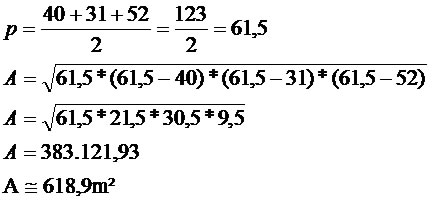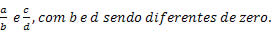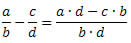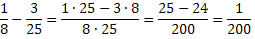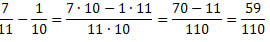Professor de Matemática Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Quíton, um exemplo de molusco pertencente à classe Polyplacophora
Caracóis, caramujos, ostras, lesmas, polvos. Todos esses animais pertencem ao filo Mollusca. O nome do grupo já fornece uma pista sobre uma característica compartilhada por todos eles. Mollusca vem do latim Mollis, que significa "mole". Todos os moluscos possuem corpo mole, recoberto ou não por uma concha calcária.
O filo dos moluscos apresenta um grande número de espécies, ficando atrás apenas dos artrópodes. Eles podem ser encontrados em ambientes marinhos, de água doce ou terrestres. Muitos moluscos são utilizados na alimentação humana e a sua pesca ou coleta é uma importante atividade econômica de inúmeros países.
Outros, como o caramujo-gigante africano (Achatina fulica), são considerados espécies invasoras. As espécies invasoras podem competir com as espécies locais, prejudicando-as. Existe um grupo de moluscos marinhos, chamados de teredinídeos, que perfuram madeira, podendo estragar o casco de barcos, piers e outras estruturas.
Embora existam muitas e diferentes espécies de moluscos, o corpo de todos eles pode ser definido segundo um plano básico: cabeça, pé e massa visceral. A cabeça porta a boca, e pode ser extremamente reduzida em alguns grupos. O pé geralmente é uma sola achatada e muscular, situada na superfície ventral do corpo. A massa visceral corresponde a uma bolsa no interior da qual se encontram os órgãos internos. Muitas classes apresentam também uma concha que recobre e protege o corpo do animal. A concha é uma estrutura composta por carbonato de cálcio secretado por glândulas epidérmicas.
Sistema digestório e excretor
O sistema digestório dos moluscos é do tipo completo, ou seja, eles possuem boca e ânus, além de esôfago, estômago e intestino.
Muitos moluscos aquáticos se alimentam de pequenas algas que ficam presas às rochas ou outros pequenos organismos. Outros são carnívoros e chegam a se alimentar de animais de porte considerável, como ouriços, estrelas-do-mar e até mesmo outros moluscos. Porém, alguns são filtradores e retiram pequenas partículas orgânicas diretamente da água. Os moluscos terrestres, em sua maioria, se alimentam de pequenas plantas, como gramíneas, ou de partes, como folhas e flores, de plantas de maior porte.
Na boca da maioria dos moluscos não filtradores existe uma estrutura chamada rádula. A rádula assemelha-se a uma língua com inúmeros dentículos de quitina que raspam as superfícies retirando o alimento. Na boca dos cefalópodes há uma espécie de mandíbula, também quitinosa, que funciona como uma prensa para segurar o alimento.
Da boca o alimento segue pelo esôfago até atingir o estômago. No estômago existe uma região glandular que secreta enzimas digestivas. Após o estômago há um intestino longo e enrolado que, por fim, desemboca no ânus.
Os moluscos possuem um par de estruturas especializadas para a excreção, são os metanefrídios. Esses órgãos filtram as substâncias tóxicas do sangue, bem como reabsorvem aquelas que ainda podem ser aproveitadas.
Sistema respiratório
Como vimos, os moluscos apresentam uma grande variedade de formas e habitats. Portanto, as estruturas respiratórias também são muito variadas. Existem desde espécies que apresentam apenas respiração branquial, espécies que possuem brânquias e nas quais a cavidade do manto funciona como um pulmão (saco pulmonar), até espécies sem nenhuma brânquia e apenas com o saco pulmonar.
Sistema circulatório
Os moluscos possuem um coração situado na região dorsal do corpo. Do coração partem vasos sanguíneos que desembocam em cavidades chamadas de hemoceles. Das hemoceles o sangue passa para todos os tecidos do corpo. O sangue retorna ao coração passando pelas brânquias ou metanefrídios. O sangue dos moluscos possui um pigmento respiratório chamado hemocianina, cuja coloração é azulada.
Sistema nervoso e sensorial
O sistema nervoso dos moluscos é composto, basicamente, por um anel de nervos ao redor do esôfago e uma série de cordões nervosos que seguem para as demais regiões do corpo. O sistema sensorial é muito variado e depende do grupo. Alguns possuem estruturas, chamadas estatocistos, capazes de perceber variações ambientais, outros possuem tentáculos sensoriais e olhos.
A reprodução dos moluscos
Os moluscos podem ser hermafroditas ou apresentar sexos separados. A fecundação pode ser externa, com liberação dos gametas na água, ou interna. O desenvolvimento pode ser indireto, ou seja, apresentar uma fase larval, ou direto, quando do ovo já eclode forma jovem.
As diversas classes de moluscos
# Classe Aplacophora
Os aplacóforos são moluscos marinhos pouco conhecidos. Possuem corpo vermiforme e algumas espécies são capazes de viver em grandes profundidades. Em geral não ultrapassam alguns milímetros de comprimento e não possuem concha.
# Classe Monoplacophora
Os monoplacóforos também são exclusivamente marinhos e habitam águas profundas. Seu corpo é totalmente recoberto por uma concha única, vindo daí seu nome (do grego mono: um).
# Classe Polyplacophora
Os poliplacóforos são popularmente chamados de quítons e vivem aderidos a rochas nas regiões entre marés ou submersas. Sua concha é formada por uma série de oito placas sobrepostas e articuladas, por isso o nome Polyplacophora (do grego polys: muito).
# Classe Scaphoda
Os escafópodos são exclusivamente marinhos e a maioria vive enterrada na areia ou lodo. São popularmente conhecidos como concha-dente. Isso porque possuem uma concha cilíndrica que lembra um dente, ou presa. O pé desses animais é musculoso e adaptado a escavar o substrato.
# Classe Bivalvia
Os bivalves são um grupo grande e muito diverso. Existem espécies marinhas e de água doce. Alguns exemplos são as ostras, os mexilhões e os mariscos. Possuem uma concha composta por duas partes, chamadas de valvas, articuladas por uma espécie de dobradiça situada na região dorsal. Possuem uma cabeça reduzida e um pé estreito que lembra a forma de um machado.
São espécies de bivalves que produzem as pérolas. Estas nada mais são do que um corpo estranho que penetra entre a concha e o manto do molusco. Como forma de proteção, as glândulas epidérmicas vão envolvendo este objeto com camadas de uma substância lisa chamada nácar, originando uma bolinha brilhante que corresponde à pérola.
# Classe Gastropoda
Os gastrópodes representam o maior grupo dentro dos moluscos. Existem espécies de água doce, marinhas e terrestres. Alguns gastrópodes bem conhecidos são as lesmas, os caracóis de jardim e os caramujos. Existem espécies com concha, geralmente espiralada, como os caracóis e caramujos, ou sem, como as lesmas. O nome do grupo faz referência ao seu pé dorsal e musculoso, situado abaixo do estômago (do grego gastros, estômago, e podos, pé).
# Classe Cephalopoda
Os cefalópodes são exclusivamente marinhos e incluem as lulas, sépias, náutilos e polvos. A concha pode estar presente, como nos náutilos, ou ausente, como é o caso dos polvos, ou ser reduzida e interna, como ocorre com as lulas e sépias. Ao redor da cabeça geralmente há um círculo de tentáculos que atua na movimentação e captura de alimentos.
Muitas espécies possuem células especiais e pigmentadas chamadas cromatóforos, que permitem a esses animais mudar de coloração. Alguns cefalópodes, como as lulas, também são dotados de um pequeno órgão, em forma de saco, que contém um fluído escuro. Quando ameaçados, esses animais liberam o fluído, dificultando a visão do predador.
*Alice Dantas Brites é professora de biologia.