terça-feira, 14 de julho de 2020

Reunião do Articulador gestar comprof Edvan para planejamento

Posted by on Nenhum comentário:
Marcadores:

Relação de Girard

Relações de Girard

Considere a função polinomial

F(x) = a0. xn + a1. xn – 1 + a2. xn – 2 +... + an – 1. x + an, sendo a0 ≠ 0 e n ≥ 1.
Considerando o teorema da decomposição podemos representar F(x) = a0 . (x – r1) . (x – r2) . ... . (x – rn).
Empregando a propriedade distributiva, tornando redutíveis os termos semelhantes, e ordenando o polinômio, temos:

F(x) = a0 . xn – a0(r1 + r2 + ... + rn) . xn-1 + a0 (r1r2 + r1r3 + ...) xn-2 + ...

Se igualarmos os coeficientes deste último polinômio, dois a dois, respectivamente, como os coeficientes iniciais a0, a1, a2, ..., an, obtemos n relações entre as raízes e os coeficientes de F, tais relações são denominadas Relações de Girard, e são as seguintes:



Relações de Girard para uma equação de grau 2

A equação a0x2 + a1 x + a2 = 0 possue como raízes os termos r1 e r2, nesse caso:




Relações de Girard para uma equação de grau 3

A equação a0x3 + a1x2 + a2x + a3 = 0 possui como raízes os termos r1, r2 e r3, nesse caso:



Relações de Girard para uma equação de grau 4

A equação a0x4 + a1x3 + a2x2 + a3x + a4 = 0 possui como raízes os termos r1, r2, r3 e r4, nesse caso:


extraido de www.colegioweb.com.br
Posted by on Nenhum comentário:
Marcadores:

Minha apresentação de slides Atividade do Gestar

Posted by on Nenhum comentário:
Marcadores:

Demonstração do Teorema de Heron

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com        

www.accbarrosogestar.wordpress.com

      

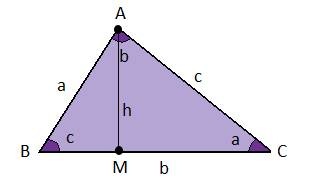
A fórmula tradicional de cálculo da área do triângulo, ensinada e muito utilizada no ensino fundamental é . Entretanto, outras fórmulas foram desenvolvidas para realizar este cálculo. Uma delas é a fórmula de Herão (ou de Heron), que dá a área do triângulo em função da medida dos três lados do triângulo. O nome faz referência ao matemático grego Herão de Alexandria.



Primeiro, encontramos o cosseno do ângulo c. Para isso, aplicamos o Teorema de Pitágoras no triângulo ABM para encontrar o comprimento de BM:







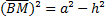
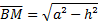
Assim,



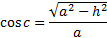
Agora, utilizando o triângulo ABC, aplicamos a lei dos cossenos relativa ao ângulo c:







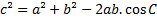
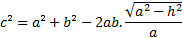
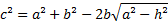
Logo,



Assim,



Substituindo (I) em (II), temos:









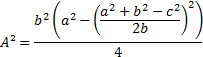
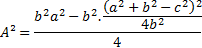
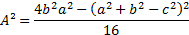
Aplicando a diferença de dois quadrados:







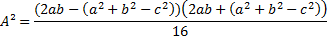
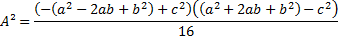
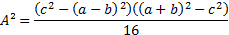
Novamente pela diferença entre quadrados:











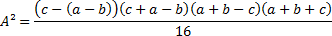
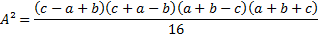
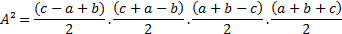
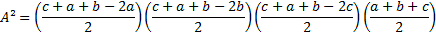
Como , tal que s é o semiperímetro (metade do perímetro), vem:



E por fim,


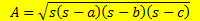
http://www.fazendomatematica.com
Posted by on 5 comentários:
Marcadores:

Logica-proposição


Professor de Matemática e Ciências Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Blog HTTP://ensinodematemtica.blogspot.com.br e http://accbarrosogestar.blogspot.com.brCONCEITO DE PROPOSIÇÃO
PROPOSIÇÃO: sentenças declarativas afirmativas (expressão de uma linguagem) da qual tenha sentido afirmar que seja verdadeira ou que seja falsa.
· A lua é quadrada.
· A neve é branca.
· Matemática é uma ciência.
Não serão objeto de estudo as sentenças interrogativas ou exclamativas.
OS SÍMBOLOS DA LINGUAGEM DO CÁLCULO PROPOSICIONAL
· VARIÁVEIS PROPOSICIONAIS: letras latinas minúsculas p,q,r,s,.... para indicar as proposições (fórmulas atômicas) .
Exemplos: A lua é quadrada : p
A neve é branca : q
· CONECTIVOS LÓGICOS: As fórmulas atômicas podem ser combinadas entre si e, para representar tais combinações usaremos os conectivos lógicos :
























Ù: e , Ú: ou , ® : se...então , « : se e somente se , ~: não Exemplos: · A lua é quadrada e a neve é branca. : p Ù q (p e q são chamados conjunctos) · A lua é quadrada ou a neve é branca. : p Ú q ( p e q são chamados disjunctos)
· Se a lua é quadrada então a neve é branca. : p ® q ( p é o antecedente e q o conseqüente)
· A lua é quadrada se e somente se a neve é branca. : p « q
· A lua não é quadrada. : ~p

 · SÍMBOLOS AUXILIARES : ( ) , parênteses que servem para denotar o "alcance" dos conectivos;
Exemplos:
























· Se a lua é quadrada e a neve é branca então a lua não é quadrada. :
((p Ù q) ® ~ p) · A lua não é quadrada se e somente se a neve é branca. :
((~ p) «q)) · DEFINIÇÃO DE FÓRMULA : 1. Toda fórmula atômicaé uma fórmula.
2. Se A e B são fórmulas então
(A Ú B) , (A Ù B) , (A ® B) , (A « B) e (~ A) também são fórmulas.
3. São fórmulas apenas as obtidas por 1. e 2. . Os parênteses serão usados segundo a seguinte ordem dos conectivos: ~, Ú , Ù , ®, « .
Com o mesmo conectivo adotaremos a convenção pela direita.
Exemplo: a fórmula p Ú q Ù ~ r ® p ® ~ q deve ser entendida como
(((p Ú q) Ù (~ r)) ® ( p ® (~ q)))
AS TABELAS VERDADE
A lógica clássica é governada por três princípios (entre outros) que podem ser formulados como segue:
· Princípio da Identidade: Todo objeto é idêntico a si mesmo.
· Princípio da Contradição: Dadas duas proposições contraditórias (uma é negação da outra), uma delas é falsa.
· Princípio do Terceiro Excluído: Dadas duas proposições contraditórias, uma delas é verdadeira.
Com base nesses princípios as proposições simples são ou verdadeiras ou falsas - sendo mutuamente exclusivos os dois casos; daí dizer que a lógica clássica é bivalente.
Para determinar o valor (verdade ou falsidade) das proposições compostas (moleculares), conhecidos os valores das proposições simples (atômicas) que as compõem usaremos tabelas-verdade :
1.Tabela verdade da "negação" : ~p é verdadeira (falsa) se e somente se p é falsa (verdadeira).
p ~p
V F
F V
2. Tabela verdade da "conjunção" : a conjunção é verdadeira se e somente os conjunctos são verdadeiros.
p
q
p Ù q
V
V
V
V
F
F
F
V
F
F
F
F
3. Tabela verdade da "disjunção" : a disjunção é falsa se, e somente, os disjunctos são falsos.
p
q
p Ú q
V
V
V
V
F
V
F
V
V
F
F
F
4. Tabela verdade da "implicação": a implicação é falsa se, e somente se, o antecedente é verdadeiro e o conseqüente é falso.
p
q
p ® q
V
V
V
V
F
F
F
V
V
F
F
V
5. Tabela verdade da "bi-implicação": a bi-implicação é verdadeira se, e somente se seus componentes são ou ambos verdadeiros ou ambos falsos
p
q
p « q
V
V
V
V
F
F
F
V
F
F
F
V
Exemplo: Construir a tabela verdade da fórmula : ((p Ú q) ® ~p) ® (q Ù p)
p
q
((p Ú q) ® ~p) ® (q Ù p)
V
V
V
F
F
V
 V
V
F
V
F
F
V
 F
F
V
V
V
V
F
 F
F
F
F
V
V
F
 F
·NÚMERO DE LINHAS DE UMA TABELA-VERDADE: Cada proposição simples (atômica) tem dois valores V ou F, que se excluem. Para n atômicas distintas, há tantas possibilidades quantos são os arranjos com repetição de 2 (V e F) elementos n a n. Segue-se que o número de linhas da tabela verdade é 2n. Assim, para duas proposições são 22 = 4 linhas; para 3 proposições são 23 = 8; etc.
Exemplo: a tabela - verdade da fórmula ((p Ù q) ® r) terá 8 linhas como segue :
p
q
r
((p Ù q) ® r )
V
V
V
V V
V
V
F
V F
V
F
V
F V
V
F
F
F V
F
V
V
F V
F
V
F
F V
F
F
V
F V
F
F
F
F V
NOTA: "OU EXCLUSIVO" É importante observar que "ou" pode ter dois sentidos na linguagem habitual: inclusivo (disjunção) Ú ("vel") e exclusivo Ú ( "aut") onde p Úq significa ((p Ú q) Ù~ (p Ù q)).
p
q
 ((p Ú q) Ù ~ (p Ù q))
V
V
 V F F V
V
F
 V V V F
F
V
 V V V F
F
F
 F F V F
Posted by on Nenhum comentário:
Marcadores:

Teorema de Tales

Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
www.youtube.com/accbarroso1

Teorema de Tales

Tales nasceu na cidade de Mileto, colônia grega localizada na Ásia menor. Filósofo, Matemático, Astrônomo, desenvolveu uma teoria que ficou conhecida como: Teorema de Tales.
Tales ficou conhecido por ter medido a altura de uma pirâmide com base no comprimento de sua sombra. Ele concluiu que os raios solares chegam à Terra inclinados, partindo dessa afirmação ele conseguiu medir a altura da pirâmide da seguinte forma: Fincou uma estaca ao lado da pirâmide e observou que no instante em que o comprimento da sombra da estaca era igual à medida do comprimento da estaca, a altura da pirâmide teria o mesmo comprimento da sua sombra.


Feixes de retas paralelas cortadas por retas transversais formam segmentos proporcionais.
Veja ilustração do Teorema de Tales:

Exemplo 1
Calcule o valor de x na ilustração abaixo

4x = 15
x = 15/4
x = 3,75

Exemplo 2
Aplique o Teorema de Tales e calcule o valor de x.

6(2x-3) = 5(x+2)
12x – 18 = 5x + 10
12x – 5x = 10 + 18
7x = 28
x = 28/7
x = 4
Posted by on 4 comentários:
Marcadores:

Feche a caixa (multiplicação)

MATERIAL: Tabuleiro, 40 marcadores e dois dados (1 de 6 faces e 1 de 10 faces)
REGRAS:
1. Distribuir o material para as duas equipes.
2. Decidir qual das equipes iniciará o jogo.
3. O jogador joga os dois dados e multiplica os números obtidos.
4. O jogador poderá cobrir (fechar) a casa com o resultado obtido ou com as casas correspondentes a decomposição do resultado na soma de dois ou mais números.
5. Vence a equipe que cobrir todas as casas do seu tabuleiro.
Observações:
1. Uma alternativa para o jogo é cobrir apenas um dos lados da caixa, não considerando o lado pintado.
2. Se depois de três jogadas de uma equipe, nenhuma casa for coberta, encerra-se o jogo. Ganha a equipe que estiver com maior número de pontos através dos valores das casas fechadas.
http://www.ibilce.unesp.br/
Posted by on Nenhum comentário:
Marcadores:

Cor - As Cores

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com          
www.youtube.com/accbarroso1     

Thiago Ribeiro

Você Conhece as Cores?
O que é a Cor?
A cor é uma sensação de luz que temos sobre nossos olhos, pois são provocados por um feixe de fótons sobre as células especializadas da retina, a cor de algo é determinada pelas médias de frequências que a onda de suas moléculas constituintes refletem.
Exemplo:
Você está vendo este objeto vermelho?
Então...
Na verdade, um objeto é vermelho se absorve todas as frequências de cores fora do vermelho.
A cor é relacionada com os diferentes comprimento de onda do espectro eletromagnético, por exemplo:
A Luz Solar (Raio de Sol), possui todas as cores possíveis, tente provar... Pegue um prisma e ponha diante dele e você verá uma espécie de arco-íris, contendo várias cores.
Assim se prova, o branco é a combinação de todas cores possíveis e o preto é a ausência delas.
Cores Primárias?
São as cores básicas que são encontradas na natureza e são impossíveis de serem decompostas e ao se misturarem forma outras cores, as chamadas cores secundárias.
São elas:
- Amarelo
- Azul
- Vermelho
Algumas cores secundárias:
- Verde (amerelo + azul);
- Laranja (vermelho + amarelo);
- Violeta (vermelho + azul).
Posted by on 2 comentários:
Marcadores:

Poliedros planificados

Imagens e figuras geométricas para imprimir

São um total de 77 imagens geométricas para imprimir os moldes sólidos geométrico é uma figura geométrica que possui as dimensões de latitude, longitude e altitude. Os sólidos são, por exemplo, a esfera, o cubo, o cilindro, o cone e a pirâmide.

Imagens e figuras geométricas para imprimir

Imagens e figuras geométricas para imprimir
Imagens e figuras geométricas para imprimir




































Fonte:www.educarx.blogspot.com.br
Posted by on Nenhum comentário:
Marcadores: ,
Assinar: Postagens (Atom)