terça-feira, 3 de dezembro de 2019
Equação modular
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Utilizando a definição de módulo que diz:
| x | = x, se x for maior ou igual a zero.
| x | = – x, se x for menor que zero.
Podemos resolver equações modulares, uma vez que:
Se | x | = k, então x = k ou x = – k.
Exemplo 1. Resolva a equação | 2x – 5 | = 7.
Solução: Da definição de módulo, temos que:
2x – 5 = 7 ou 2x – 5 = – 7
2x = 7 + 5 2x = – 7 + 5
2x = 12 2x = – 2
x = 6 x = – 1
Portanto, S = {– 1, 6}
Exemplo 2. Resolva a equação |x2 + 4x + 5| = 5
Solução: Temos que
x2 + 4x + 5 = 5 ou x2 + 4x + 5 = – 5
x2 + 4x + 5 – 5 = 0 x2 + 4x + 5 + 5 = 0
x2 + 4x = 0 x2 + 4x + 10 = 0
x(x + 4) = 0 Δ = 16 – 40 = – 24
x = 0 ou x = – 4 não possui solução real, pois Δ < 0
Portanto, S = {– 4, 0}
Exemplo 3. Determine o conjunto solução da equação:
| x |2 – 8| x | – 9 = 0
Solução: Nesse caso, devemos fazer uma mudança de variável.
| x | = y
Substituindo na equação inicial, obtemos:
y2 – 8y – 9 = 0
Δ = (– 8)2 – 4*1*(– 9) = 64 + 36 = 100
y = 9 ou y = – 1
Daí, temos que:
| x | = 9 → x = 9 ou x = – 9
| x | = – 1 → não faz sentido, uma vez que o módulo de um número é sempre um valor positivo.
Portanto, S = { - 9, 9}
www.bancodeconcursos.com
Gráfico de Inequações do 1º Grau
Professor de Matemática Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Diferente das equações, as inequações são expressões matemáticas que apresentam em sua configuração sinais de desigualdade. Veja:>: maior que
<: menor que
≥: maior ou igual que
≤: menor ou igual que
As inequações são utilizadas em cálculos envolvendo restrições ao valor da incógnita. Por exemplo, ao resolvermos a equação 2x + 5 > 11, descobrimos que seu valor é correspondente a x > 3, de modo a respeitar a condição da inequação.
Os sinais de desigualdade podem ser utilizados em qualquer expressão matemática envolvendo incógnitas, como funções do 1º grau, do 2º grau, exponenciais, logarítmicas, trigonométricas, modulares.
As inequações também possuem gráficos representados no plano cartesiano. Na construção deles devemos levar em consideração o sinal da desigualdade.
Exemplo 1
Vamos determinar a construção do gráfico da seguinte expressão: 2x + 4 ≤ 0.
y = 0
2x + 4 ≤ 0
2x ≤ – 4
x ≤ –2
Gráfico
Exemplo 2
Construir o gráfico da inequação x + 4 ≥ 0, de acordo com a raiz da função.
y = 0
x + 4 ≥ 0
x ≥ – 4
Gráfico
Exemplo 3
Determinando o gráfico da inequação –2x + 7 > 0.
–2x + 7 > 0
–2x > –7
x < –7/2
x < –3,5
Gráfico
Marcos Noé Pedro da Silva
Sistemas e Equações Lineares
Equações Lineares
As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente.
A equação 4x – 3y + 5z = 31 é uma equação linear. Os coeficientes são 4, –3 e 5; x, y e z as incógnitas e 31 o termo independente.
Para x = 2, y = 4 e z = 7, temos 4*2 – 3*4 + 5*7 = 31, concluímos que o terno ordenado (2,4,7) é solução da equação linear
4x – 3y + 5z = 31.
Para x = 1, y = 0 e z = 3, temos 4*1 – 3*0 + 5*3 ≠ 31, concluímos que o terno ordenado (1,0,3) não é solução da equação linear
4x – 3y + 5z = 31.
www.mundoeducacao.com.br
Sistemas Lineares
Dizemos que o conjunto de equações lineares forma um sistema linear.
Exemplos
2x + 3y = 10
x – 5y = 2Sistema linear com duas equações e duas incógnitas.
5x – 6y – 2z = 15
9x – 10y + 5z = 20Sistema linear com duas equações e três incógnitas.
x + 9y + 6z = 20
3x – 10y – 12z = 5
-x + y + z = 23Sistema linear com três equações e três incógnitas.
x+ y + z + w = 36
2x – y +2z + 9w = 40
-5x + 3y – 5z + 5w = 16Sistema linear com três equações e quatro incógnitas.
O sistema linear abaixo admite o terno ordenado (1, 2, 3) como solução.
x + 2y – z = 2
2x – y + z = 3
x + y + z = 6
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 3 = 6 → 6 = 6
No entanto, ele não admite como solução o terno ordenado (1, 2, 4).
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 4 = 6 → 7 ≠ 6
As equações do tipo a1x1 + a2x2 + a3x3 + .....+ anxn = b, são equações lineares, onde a1, a2, a3, ... são os coeficientes; x1, x2, x3,... as incógnitas e b o termo independente.
A equação 4x – 3y + 5z = 31 é uma equação linear. Os coeficientes são 4, –3 e 5; x, y e z as incógnitas e 31 o termo independente.
Para x = 2, y = 4 e z = 7, temos 4*2 – 3*4 + 5*7 = 31, concluímos que o terno ordenado (2,4,7) é solução da equação linear
4x – 3y + 5z = 31.
Para x = 1, y = 0 e z = 3, temos 4*1 – 3*0 + 5*3 ≠ 31, concluímos que o terno ordenado (1,0,3) não é solução da equação linear
4x – 3y + 5z = 31.
www.mundoeducacao.com.br
Sistemas Lineares
Dizemos que o conjunto de equações lineares forma um sistema linear.
Exemplos
2x + 3y = 10
x – 5y = 2Sistema linear com duas equações e duas incógnitas.
5x – 6y – 2z = 15
9x – 10y + 5z = 20Sistema linear com duas equações e três incógnitas.
x + 9y + 6z = 20
3x – 10y – 12z = 5
-x + y + z = 23Sistema linear com três equações e três incógnitas.
x+ y + z + w = 36
2x – y +2z + 9w = 40
-5x + 3y – 5z + 5w = 16Sistema linear com três equações e quatro incógnitas.
O sistema linear abaixo admite o terno ordenado (1, 2, 3) como solução.
x + 2y – z = 2
2x – y + z = 3
x + y + z = 6
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 3 = 6 → 6 = 6
No entanto, ele não admite como solução o terno ordenado (1, 2, 4).
1 + 2*2 – 3 = 2 → 1+ 4 – 3 = 2 → 2 = 2
2*1 – 2 + 3 = 3 → 2 – 2 + 3 = 2 → 3 = 3
1 + 2 + 4 = 6 → 7 ≠ 6
Fatoração
As fatorações são utilizadas no intuito de transformar expressões e equações algébricas em procedimentos envolvendo o produto de duas ou mais expressões. Dessa forma, em algumas situações, as equações podem ser resolvidas de forma simples e direta. Para a realização da fatoração simultânea, o conhecimento das técnicas envolvendo termo comum em evidência, agrupamento, diferença entre dois quadrados, trinômio quadrado perfeito e trinômio soma e produto, é de extrema importância. Em alguns polinômios, a fatoração por completo exige a utilização de duas ou mais técnicas informadas.
Observe alguns exemplos envolvendo a utilização da fatoração simultânea:
Exemplo 1
x³ + 2x² + x
1ª fatoração: fator comum em evidência
x * (x² + 2x + 1)
2ª fatoração: trinômio quadrado perfeito
x * (x + 1)²
x³ + 2x² + x → x * (x + 1)²
Exemplo 2
a²x – b²x
1ª fatoração: fator comum em evidência
x * (a² – b²)
2ª fatoração: diferença entre dois quadrados
x * (a + b) * (a – b)
a²x – b²x → x * (a + b) * (a – b)
Exemplo 3
x²b + 5bx + 6b
1ª fatoração: fator comum em evidência
b * (x² + 5x + 6)
2ª fatoração: trinômio soma e produto
b * (x + 2) * (x + 3)
x²b + 5bx + 6b → b * (x + 2) * (x + 3)
Exemplo 4
4x³ + 3x² – 4y²x – 3y²
1ª fatoração: agrupamento
x² * (4x + 3) – y² * (4x + 3)
(x² – y²) * (4x + 3)
2ª fatoração: diferença entre dois quadrados
(x + y) * (x – y) * (4x + 3)
4x³ + 3x² – 4y²x – 3y² → (x + y) * (x – y) * (4x + 3)
Exemplo 5
a³ – a
1ª fatoração: fator em evidência
a * (a² – a)
2ª fatoração: diferença entre dois quadrados
a * (a + 1 ) * (a – 1)
a³ – a → a * (a + 1 ) * (a – 1)
Exemplo 6
12x³ – 3xy²
1ª fatoração: fator em evidência
3x * (4x² – y²)
2ª fatoração: agrupamento
3x * (2x – y) * (2x + y)
12x³ – 3xy² → 3x * (2x – y) * (2x + y)
Fatorar é o mesmo que decompor o número em fatores primos, isto é, escrever um número através da multiplicação de números primos. Na fatoração utilizamos os números primos obedecendo a uma ordem crescente de acordo com as regras de divisibilidade em razão do termo a ser fatorado. Números primos são aqueles que podem ser divididos somente por um e por ele mesmo. Observe a decomposição em fatores primos dos números a seguir:
24 = 2 x 2 x 2 x 3
10 = 2 x 5
52 = 2 x 2 x 13
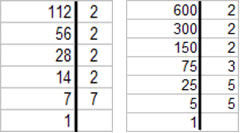
112 = 2 x 2 x 2 x 2 x 7
600 = 2 x 2 x 2 x 3 x 5 x 5
Forma prática de fatoração
O número a ser fatorado deverá ocupar a coluna da esquerda e a coluna da direita será preenchida com os fatores primos. Ao dividir o número pelo algarismo primo os resultados deverão ser colocados na coluna da direita. As divisões deverão ser efetuadas no intuito de simplificar ao máximo o número, isto é reduzi-lo ao número 1.
.jpg)
Objetivos da fatoração
Cálculo da raiz quadrada de um número.
Vamos determinar a raiz quadrada do número 144.
De acordo com a fatoração do número 144 temos: 2 x 2 x 2 x 2 x 3 x 3.
No caso da raiz quadrada, podemos representar o número 144 da seguinte forma:
2² x 2² x 3². Como o índice da raiz quadrada é 2, podemos simplificar os expoentes de valor 2 com o índice 2 da raiz. As bases dos expoentes simplificados saem da raiz multiplicadas entre si. Acompanhe a demonstração a seguir:
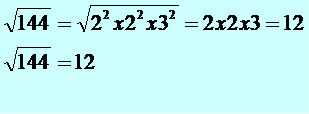.jpg)
Dado dois números quaisquer x e y. Se subtrairmos ficará: x – y, se montarmos uma expressão algébrica com os dois números obteremos: x2 + xy + y2, assim, devemos multiplicar as duas expressões encontradas.
(x - y) (x2 + xy + y2) é necessário utilizar a propriedade distributiva;
x3 + x2y + xy2 - x2y –xy2 - y3 unir os termos semelhantes;
x3 - y3 é uma expressão algébrica de dois termos, os dois estão elevados ao cubo e subtraídos.
Assim, podemos concluir que x3 - y3 é uma forma geral da soma de dois cubos onde
x e y podem assumir qualquer valor real.
A forma fatorada de x3 - y3 será (x - y) (x2 + xy + y2).
Com o conhecimento de todos os casos de fatoração, quando for preciso fatorar alguma expressão algébrica devemos sempre observar em qual dos casos ela se enquadra, veja os exemplos de como fazer esse reconhecimento.
Exemplo:
Se tivermos que fatorar a seguinte expressão algébrica 27x3 – y3 devemos observar que ela tem dois termos. Lembrando dos casos de fatoração, o único caso que fatora dois termos é a diferença de dois quadrados, soma de dois cubos e a diferença de dois cubos.
No exemplo acima os dois termos estão ao cubo e entre eles há uma subtração, então devemos utilizar o 7º caso de fatoração (diferença de dois cubos), para fatorarmos devemos escrever a expressão algébrica 27x3 – y3 da seguinte forma:
(x - y) (x2 + xy + y2). Ao tirar as raízes cúbicas dos dois termos, temos: 27x3 – y3.
A raiz cúbica de 27x3 é 3x e a raiz cúbica de y3 é y. Agora, basta substituir valores, no lugar de x colocaremos 2x e no lugar de y colocaremos 3 na forma fatorada
(x - y) (x2 + xy + y2) , ficando assim:
(3x – y) ((3x)2 + 3x . y + y2)
(3x – y) (9x2 + 3xy + y2)
Então, (2x – 3) (4x2 + 6x + 9) é a forma fatorada da expressão algébrica 8x3 – 27.
Exemplo 2
Para resolvemos a fatoração utilizando a diferença de dois cubos devemos seguir os mesmos passos do exemplo anterior. Fatorando a expressão algébrica r3 – 64 temos: As raízes cúbicas de r3 é r e de 64 é 4, substituindo teremos no lugar de x o r e no lugar de y o 4.
(r – 4) (r2 + 4r + 16) é a forma fatorada de r3 – 64.
Dado dois números quaisquer x e y, se somarmos os dois obteremos x + y, se montarmos uma expressão algébrica com os dois números teremos x2 - xy + y2, agora devemos multiplicar as duas expressões encontradas.
(x + y) (x2 - xy + y2) utilize a propriedade distributiva;
x3 - x2y + xy2 + x2y –xy2 + y3 una os termos semelhantes;
x3 + y3 é uma expressão algébrica de dois termos onde os dois estão elevados ao cubo e somados.
Assim, podemos concluir que x3 + y3 é uma forma geral da soma de dois cubos onde
x e y poderão assumir qualquer valor real.
A forma fatorada de x3 + y3 será (x + y) (x2 - xy + y2).
Veja alguns exemplos:
Exemplo1:
27x3 + 1000 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
33x3 + 103, assim: x = 3x e y = 10
Agora, basta usarmos a forma geral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(3x + 10) ((3x)2 – 3x . 10 + 102)
(3x + 10) (9x2 – 30x + 100)
Portanto, a fatoração de 27x3 + 1000 será (3x + 10) (9x2 – 30x + 100).
Exemplo 2:
x3 + 1 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
(x)3 + 13 assim: x = x e y = 1
Agora, basta usarmos a forma gral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(x + 1) ((x)2 –x .1 + 12)
(x – 1) (x2 –x + 1)
Exemplo 3:
8x3 + y3 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
(2x)3 + y3 assim: x = 2x e y = y
Agora, basta usarmos a forma gral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(2x + y) ((2x)2 – 2xy + y2)
(2x + y) (4x2 – 2xy + y2)
Para fatorar uma expressão algébrica utilizando esse primeiro caso de fatoração, todos os monômios da expressão algébrica devem ter pelo menos algum termo em comum.
A fatoração é feita colocando o termo comum em evidência, veja alguns exemplos:
►a – ab é uma expressão algébrica, veja como devemos fatorar:
É preciso analisar se o 1º caso poderá ser utilizado para a fatoração, então é necessário analisar todos os seus monômios (termos) para ver se há termos em comum.
a – ab essa expressão tem dois monômios a e ab
Os dois possuem termos semelhantes: o termo semelhante é a. Então, colocamos esse termo comum em evidência.
Quando colocamos a em evidência devemos dividir a e ab (os monômios) por a (termo comum), assim:
a : a = 1, pois todo número (ou letra) dividido por ele mesmo é igual a 1.
ab : a = b, pois a : a = 1, então ficaria 1b que é o mesmo que b.
Portanto a – ab = a (1 – b)
↓
Termos
em evidência
►a3 – 4a2 é uma expressão algébrica, veja como fatorar:
Essa expressão algébrica tem 2 monômios a3 e 4a2, eles têm o a como termo semelhante, então podemos colocá-lo em evidência, mas poderá surgir uma dúvida, devemos colocar o a3 ou a2? Devemos colocar sempre o de menor expoente, então colocamos a2.
Assim, devemos dividir a3 e 4a2 por a2, assim:
a3 : a2 = a, pois a3 = a .a .a, então a . a . a : a2 é o mesmo que 1a = a.
4a2 : a2 = 4, pois a2 : a2 = 1, então ficaria 4 . 1 que é mesmo que 4.
Portanto a3 – 4a2 = a2 (a – 4).
↓
Termos
em evidência
►x4 - 2x3 + x2 + x é uma expressão algébrica que tem quatro monômios, eles têm termos em comum, como esses termos têm mesma base devemos pegar o de menor expoente, então o termo em comum é x.
O termo em evidência deverá ser dividido pelos monômios x4 , 2x2 , x2 e x, assim:
x4 : x = x3, pois em bases iguais conservamos a base e diminuímos os expoentes.
2x3 : x = 2x2, pois em bases iguais conservamos a base e diminuímos os expoentes.
x2 : x = x, pois em bases iguais conservamos a base e diminuímos os expoentes.
x : x = 1, pois qualquer número ou letra dividido por ele mesmo é igual a 1.
Portanto x4 - 2x3 + x2 + x = x (x3 – 2x2 + x – 1).
↓
Termos
em evidência
► 4r + 12 é uma expressão algébrica, olhando rapidamente podemos pensar que não existe termo semelhante, o que seria errado, pois o número 12 pode ser fatorado em dois fatores 12 = 4 . 3, com essa fatoração percebemos que há um termo em comum na expressão algébrica, esse é o 4.
Então, pegamos os monômios 4r e 12 e dividimos por 4, ficando assim:
4r : 4 = 1r ou r
12 : 4 = 3
Portanto, 4r + 12 = 4 (r + 3)
↓
Termos
em evidência
► Para fatorarmos a expressão algébrica (x + 1) (x – 3) + 2 (x + 1) devemos ter um pouco mais de cuidado, pois em primeiro lugar separamos os termos:
(x + 1) (x – 3) + 2 (x + 1) a expressão possui dois termos.
↓ ↓
1º termo 2º termo
O termo semelhante é (x + 1), pois é encontrado tanto no 1º termo, como no 2º.
Então, devemos dividir o 1º termo e o 2º por (x + 1), ficando assim:
[(x + 1) (x – 3)] : (x + 1) = (x – 3)
2 (x + 1) : (x + 1) = 2
Portanto, (x + 1) (x – 3) + 2 (x + 1) = (x + 1) (x – 3 + 2)
(x + 1) (x – 3) + 2 (x + 1) = (x + 1) (x – 1)
↓
Termos
em evidência
Para conferir se as fatorações estão corretas, basta efetuar as fatorações, veja:
Para verificar se a fatoração 4r + 12 = 4 (r + 3) está correta, basta pegar a expressão algébrica fatorada 4 (r + 3) e resolvê-la:
Aplicando a propriedade distributiva temos: 4 (r + 3) = 4 . r + 4 . 3 = 4r + 12. Podemos concluir que a fatoração está correta.
Quando aplicamos o caso de fatoração por agrupamento, utilizamos a fatoração por termos comuns. Veja:
Se observarmos a expressão ab + 3b + 7a + 21 veremos que não são todos os monômios que têm termos semelhantes, mas podemos unir os que possuem termos semelhantes.
Assim, temos: ab + 3b + 7a + 21, agora aplicamos o 1º caso de fatoração (termo comum), colocando em evidência cada elemento comum de cada agrupamento.
ab + 3b + 7a + 21
↓ ↓
b termo 7 é o termo comum
comum
Então: b (a + 3) + 7 (a + 3)
Mesmo fazendo essa fatoração observamos que ainda podemos fazer mais uma fatoração, pois os dois termos b (a + 3) e 7 (a + 3) possuem um termo em comum
(a + 3). Então, aplicamos o processo do fator comum, ficando assim a fatoração:
b (a + 3) + 7 (a + 3)
(a + 3) (b + 7)
Portanto, a expressão algébrica ab + 3b + 7a + 21 fatorada fica assim: (a + 3) (b + 7).
Dada a expressão algébrica y2 – 5y + 6, sabemos que é um trinômio, mas os seus dois membros das extremidades não estão elevados ao quadrado, assim descarta a possibilidade de ser quadrado perfeito.
Então, o único caso de fatoração que podemos utilizar para fatorar essa expressão algébrica é x2 + Sx + P. Dada a expressão y2 – 5y + 6, observe se ela está em ordem decrescente de seus expoentes (do maior para o menor), se estiver basta achar dois números que somados resultem em -5 e que o produto deles resulte em 6.
Vamos fazer as tentativas para que o produto resulte em 6:
2 . 3 = 6
(- 2) . (- 3) = 6
6 . 1= 6
- 6 . (- 1) = 6
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê -5. Concluímos que -2 + (-3) = -5, portanto a forma fatorada desse trinômio será:
(y – 2) (y – 3).
Dada a expressão m2 + 7m – 8, devemos achar dois números que somados resulte 7 e o produto deles seja -8. Verificamos as possibilidades do produto resultar em - 8:
- 1 . 8 = - 8
1 . (-8) = - 8
4 . (- 2) = - 8
- 4 . 2 = - 8
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê 7. Concluímos que -1 + 8 = 7, portanto a forma fatorada desse trinômio será:
(m – 1) (m + 8).
Dado a expressão x2 + 4x – 12, devemos achar dois números que somados resulte em 4 e o produto do mesmo seja – 12. Verifiquemos as possibilidades de o produto resultar em -12:
1 .(-12) = -12
-1 . 12 = -12
6 . (-2) = -12
- 6 . 2 = -12
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê 4. Concluímos que 6 +(- 2) = 4, portanto a forma fatorada desse trinômio será:
(x + 6) (x – 2)
Esse caso de fatoração só pode ser utilizado em expressões algébricas que possuem dois monômios e os mesmos devem estar elevados ao quadrado (elevados à quinta potência).
Chegamos à conclusão que a diferença de dois quadrados pode ser utilizada, quando:
-Tivermos uma expressão algébrica com dois monômios (sejam binômios).
- Os dois monômios forem quadrados.
- A operação entre eles for de subtração.
Veja alguns exemplos de expressões algébricas que seguem esse modelo:
• a2 - 16
• 1 – a2
3
• 4x2 – b2
Como fazer essa fatoração
Dada a expressão algébrica 9x2 – 81, veja os passos que devemos tomar para chegarmos à forma fatorada utilizando o 5º caso de fatoração.
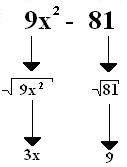
A forma fatorada será (3x – 9) (3x + 9).
Veja alguns exemplos:
Exemplo 1:
A expressão algébrica x2 – 4 é uma expressão com dois monômios e as raízes quadradas são respectivamente x e 2, então a sua forma fatorada é (x – 2) (x + 2).
Exemplo 2:
Dada a expressão algébrica 16x2 – 25, a raiz dos termos 16x2 e 25 é respectivamente 4x e 5. Então, a forma fatorada é (4x – 5) (4x + 5).
Exemplo 3:
Dada a expressão algébrica 36x2 – 81y2, a raiz dos termos 36x2 e 81y2 é respectivamente 6x e 9y. Então, a forma fatorada é (6x – 9y) (6x + 9y).
Fonte mundoeducacao.com.br
Observe alguns exemplos envolvendo a utilização da fatoração simultânea:
Exemplo 1
x³ + 2x² + x
1ª fatoração: fator comum em evidência
x * (x² + 2x + 1)
2ª fatoração: trinômio quadrado perfeito
x * (x + 1)²
x³ + 2x² + x → x * (x + 1)²
Exemplo 2
a²x – b²x
1ª fatoração: fator comum em evidência
x * (a² – b²)
2ª fatoração: diferença entre dois quadrados
x * (a + b) * (a – b)
a²x – b²x → x * (a + b) * (a – b)
Exemplo 3
x²b + 5bx + 6b
1ª fatoração: fator comum em evidência
b * (x² + 5x + 6)
2ª fatoração: trinômio soma e produto
b * (x + 2) * (x + 3)
x²b + 5bx + 6b → b * (x + 2) * (x + 3)
Exemplo 4
4x³ + 3x² – 4y²x – 3y²
1ª fatoração: agrupamento
x² * (4x + 3) – y² * (4x + 3)
(x² – y²) * (4x + 3)
2ª fatoração: diferença entre dois quadrados
(x + y) * (x – y) * (4x + 3)
4x³ + 3x² – 4y²x – 3y² → (x + y) * (x – y) * (4x + 3)
Exemplo 5
a³ – a
1ª fatoração: fator em evidência
a * (a² – a)
2ª fatoração: diferença entre dois quadrados
a * (a + 1 ) * (a – 1)
a³ – a → a * (a + 1 ) * (a – 1)
Exemplo 6
12x³ – 3xy²
1ª fatoração: fator em evidência
3x * (4x² – y²)
2ª fatoração: agrupamento
3x * (2x – y) * (2x + y)
12x³ – 3xy² → 3x * (2x – y) * (2x + y)
Fatorar é o mesmo que decompor o número em fatores primos, isto é, escrever um número através da multiplicação de números primos. Na fatoração utilizamos os números primos obedecendo a uma ordem crescente de acordo com as regras de divisibilidade em razão do termo a ser fatorado. Números primos são aqueles que podem ser divididos somente por um e por ele mesmo. Observe a decomposição em fatores primos dos números a seguir:
24 = 2 x 2 x 2 x 3
10 = 2 x 5
52 = 2 x 2 x 13
112 = 2 x 2 x 2 x 2 x 7
600 = 2 x 2 x 2 x 3 x 5 x 5
Forma prática de fatoração
O número a ser fatorado deverá ocupar a coluna da esquerda e a coluna da direita será preenchida com os fatores primos. Ao dividir o número pelo algarismo primo os resultados deverão ser colocados na coluna da direita. As divisões deverão ser efetuadas no intuito de simplificar ao máximo o número, isto é reduzi-lo ao número 1.
.jpg)
Objetivos da fatoração
Cálculo da raiz quadrada de um número.
Vamos determinar a raiz quadrada do número 144.
De acordo com a fatoração do número 144 temos: 2 x 2 x 2 x 2 x 3 x 3.
No caso da raiz quadrada, podemos representar o número 144 da seguinte forma:
2² x 2² x 3². Como o índice da raiz quadrada é 2, podemos simplificar os expoentes de valor 2 com o índice 2 da raiz. As bases dos expoentes simplificados saem da raiz multiplicadas entre si. Acompanhe a demonstração a seguir:
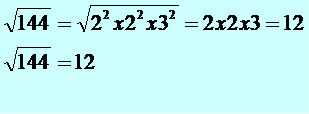.jpg)
Dado dois números quaisquer x e y. Se subtrairmos ficará: x – y, se montarmos uma expressão algébrica com os dois números obteremos: x2 + xy + y2, assim, devemos multiplicar as duas expressões encontradas.
(x - y) (x2 + xy + y2) é necessário utilizar a propriedade distributiva;
x3 + x2y + xy2 - x2y –xy2 - y3 unir os termos semelhantes;
x3 - y3 é uma expressão algébrica de dois termos, os dois estão elevados ao cubo e subtraídos.
Assim, podemos concluir que x3 - y3 é uma forma geral da soma de dois cubos onde
x e y podem assumir qualquer valor real.
A forma fatorada de x3 - y3 será (x - y) (x2 + xy + y2).
Com o conhecimento de todos os casos de fatoração, quando for preciso fatorar alguma expressão algébrica devemos sempre observar em qual dos casos ela se enquadra, veja os exemplos de como fazer esse reconhecimento.
Exemplo:
Se tivermos que fatorar a seguinte expressão algébrica 27x3 – y3 devemos observar que ela tem dois termos. Lembrando dos casos de fatoração, o único caso que fatora dois termos é a diferença de dois quadrados, soma de dois cubos e a diferença de dois cubos.
No exemplo acima os dois termos estão ao cubo e entre eles há uma subtração, então devemos utilizar o 7º caso de fatoração (diferença de dois cubos), para fatorarmos devemos escrever a expressão algébrica 27x3 – y3 da seguinte forma:
(x - y) (x2 + xy + y2). Ao tirar as raízes cúbicas dos dois termos, temos: 27x3 – y3.
A raiz cúbica de 27x3 é 3x e a raiz cúbica de y3 é y. Agora, basta substituir valores, no lugar de x colocaremos 2x e no lugar de y colocaremos 3 na forma fatorada
(x - y) (x2 + xy + y2) , ficando assim:
(3x – y) ((3x)2 + 3x . y + y2)
(3x – y) (9x2 + 3xy + y2)
Então, (2x – 3) (4x2 + 6x + 9) é a forma fatorada da expressão algébrica 8x3 – 27.
Exemplo 2
Para resolvemos a fatoração utilizando a diferença de dois cubos devemos seguir os mesmos passos do exemplo anterior. Fatorando a expressão algébrica r3 – 64 temos: As raízes cúbicas de r3 é r e de 64 é 4, substituindo teremos no lugar de x o r e no lugar de y o 4.
(r – 4) (r2 + 4r + 16) é a forma fatorada de r3 – 64.
Dado dois números quaisquer x e y, se somarmos os dois obteremos x + y, se montarmos uma expressão algébrica com os dois números teremos x2 - xy + y2, agora devemos multiplicar as duas expressões encontradas.
(x + y) (x2 - xy + y2) utilize a propriedade distributiva;
x3 - x2y + xy2 + x2y –xy2 + y3 una os termos semelhantes;
x3 + y3 é uma expressão algébrica de dois termos onde os dois estão elevados ao cubo e somados.
Assim, podemos concluir que x3 + y3 é uma forma geral da soma de dois cubos onde
x e y poderão assumir qualquer valor real.
A forma fatorada de x3 + y3 será (x + y) (x2 - xy + y2).
Veja alguns exemplos:
Exemplo1:
27x3 + 1000 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
33x3 + 103, assim: x = 3x e y = 10
Agora, basta usarmos a forma geral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(3x + 10) ((3x)2 – 3x . 10 + 102)
(3x + 10) (9x2 – 30x + 100)
Portanto, a fatoração de 27x3 + 1000 será (3x + 10) (9x2 – 30x + 100).
Exemplo 2:
x3 + 1 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
(x)3 + 13 assim: x = x e y = 1
Agora, basta usarmos a forma gral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(x + 1) ((x)2 –x .1 + 12)
(x – 1) (x2 –x + 1)
Exemplo 3:
8x3 + y3 é a soma de dois cubos.
Podemos escrever essa expressão da seguinte forma:
(2x)3 + y3 assim: x = 2x e y = y
Agora, basta usarmos a forma gral e fazermos as substituições.
(x + y) (x2 - xy + y2)
(2x + y) ((2x)2 – 2xy + y2)
(2x + y) (4x2 – 2xy + y2)
Para fatorar uma expressão algébrica utilizando esse primeiro caso de fatoração, todos os monômios da expressão algébrica devem ter pelo menos algum termo em comum.
A fatoração é feita colocando o termo comum em evidência, veja alguns exemplos:
►a – ab é uma expressão algébrica, veja como devemos fatorar:
É preciso analisar se o 1º caso poderá ser utilizado para a fatoração, então é necessário analisar todos os seus monômios (termos) para ver se há termos em comum.
a – ab essa expressão tem dois monômios a e ab
Os dois possuem termos semelhantes: o termo semelhante é a. Então, colocamos esse termo comum em evidência.
Quando colocamos a em evidência devemos dividir a e ab (os monômios) por a (termo comum), assim:
a : a = 1, pois todo número (ou letra) dividido por ele mesmo é igual a 1.
ab : a = b, pois a : a = 1, então ficaria 1b que é o mesmo que b.
Portanto a – ab = a (1 – b)
↓
Termos
em evidência
►a3 – 4a2 é uma expressão algébrica, veja como fatorar:
Essa expressão algébrica tem 2 monômios a3 e 4a2, eles têm o a como termo semelhante, então podemos colocá-lo em evidência, mas poderá surgir uma dúvida, devemos colocar o a3 ou a2? Devemos colocar sempre o de menor expoente, então colocamos a2.
Assim, devemos dividir a3 e 4a2 por a2, assim:
a3 : a2 = a, pois a3 = a .a .a, então a . a . a : a2 é o mesmo que 1a = a.
4a2 : a2 = 4, pois a2 : a2 = 1, então ficaria 4 . 1 que é mesmo que 4.
Portanto a3 – 4a2 = a2 (a – 4).
↓
Termos
em evidência
►x4 - 2x3 + x2 + x é uma expressão algébrica que tem quatro monômios, eles têm termos em comum, como esses termos têm mesma base devemos pegar o de menor expoente, então o termo em comum é x.
O termo em evidência deverá ser dividido pelos monômios x4 , 2x2 , x2 e x, assim:
x4 : x = x3, pois em bases iguais conservamos a base e diminuímos os expoentes.
2x3 : x = 2x2, pois em bases iguais conservamos a base e diminuímos os expoentes.
x2 : x = x, pois em bases iguais conservamos a base e diminuímos os expoentes.
x : x = 1, pois qualquer número ou letra dividido por ele mesmo é igual a 1.
Portanto x4 - 2x3 + x2 + x = x (x3 – 2x2 + x – 1).
↓
Termos
em evidência
► 4r + 12 é uma expressão algébrica, olhando rapidamente podemos pensar que não existe termo semelhante, o que seria errado, pois o número 12 pode ser fatorado em dois fatores 12 = 4 . 3, com essa fatoração percebemos que há um termo em comum na expressão algébrica, esse é o 4.
Então, pegamos os monômios 4r e 12 e dividimos por 4, ficando assim:
4r : 4 = 1r ou r
12 : 4 = 3
Portanto, 4r + 12 = 4 (r + 3)
↓
Termos
em evidência
► Para fatorarmos a expressão algébrica (x + 1) (x – 3) + 2 (x + 1) devemos ter um pouco mais de cuidado, pois em primeiro lugar separamos os termos:
(x + 1) (x – 3) + 2 (x + 1) a expressão possui dois termos.
↓ ↓
1º termo 2º termo
O termo semelhante é (x + 1), pois é encontrado tanto no 1º termo, como no 2º.
Então, devemos dividir o 1º termo e o 2º por (x + 1), ficando assim:
[(x + 1) (x – 3)] : (x + 1) = (x – 3)
2 (x + 1) : (x + 1) = 2
Portanto, (x + 1) (x – 3) + 2 (x + 1) = (x + 1) (x – 3 + 2)
(x + 1) (x – 3) + 2 (x + 1) = (x + 1) (x – 1)
↓
Termos
em evidência
Para conferir se as fatorações estão corretas, basta efetuar as fatorações, veja:
Para verificar se a fatoração 4r + 12 = 4 (r + 3) está correta, basta pegar a expressão algébrica fatorada 4 (r + 3) e resolvê-la:
Aplicando a propriedade distributiva temos: 4 (r + 3) = 4 . r + 4 . 3 = 4r + 12. Podemos concluir que a fatoração está correta.
Quando aplicamos o caso de fatoração por agrupamento, utilizamos a fatoração por termos comuns. Veja:
Se observarmos a expressão ab + 3b + 7a + 21 veremos que não são todos os monômios que têm termos semelhantes, mas podemos unir os que possuem termos semelhantes.
Assim, temos: ab + 3b + 7a + 21, agora aplicamos o 1º caso de fatoração (termo comum), colocando em evidência cada elemento comum de cada agrupamento.
ab + 3b + 7a + 21
↓ ↓
b termo 7 é o termo comum
comum
Então: b (a + 3) + 7 (a + 3)
Mesmo fazendo essa fatoração observamos que ainda podemos fazer mais uma fatoração, pois os dois termos b (a + 3) e 7 (a + 3) possuem um termo em comum
(a + 3). Então, aplicamos o processo do fator comum, ficando assim a fatoração:
b (a + 3) + 7 (a + 3)
(a + 3) (b + 7)
Portanto, a expressão algébrica ab + 3b + 7a + 21 fatorada fica assim: (a + 3) (b + 7).
Dada a expressão algébrica y2 – 5y + 6, sabemos que é um trinômio, mas os seus dois membros das extremidades não estão elevados ao quadrado, assim descarta a possibilidade de ser quadrado perfeito.
Então, o único caso de fatoração que podemos utilizar para fatorar essa expressão algébrica é x2 + Sx + P. Dada a expressão y2 – 5y + 6, observe se ela está em ordem decrescente de seus expoentes (do maior para o menor), se estiver basta achar dois números que somados resultem em -5 e que o produto deles resulte em 6.
Vamos fazer as tentativas para que o produto resulte em 6:
2 . 3 = 6
(- 2) . (- 3) = 6
6 . 1= 6
- 6 . (- 1) = 6
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê -5. Concluímos que -2 + (-3) = -5, portanto a forma fatorada desse trinômio será:
(y – 2) (y – 3).
Dada a expressão m2 + 7m – 8, devemos achar dois números que somados resulte 7 e o produto deles seja -8. Verificamos as possibilidades do produto resultar em - 8:
- 1 . 8 = - 8
1 . (-8) = - 8
4 . (- 2) = - 8
- 4 . 2 = - 8
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê 7. Concluímos que -1 + 8 = 7, portanto a forma fatorada desse trinômio será:
(m – 1) (m + 8).
Dado a expressão x2 + 4x – 12, devemos achar dois números que somados resulte em 4 e o produto do mesmo seja – 12. Verifiquemos as possibilidades de o produto resultar em -12:
1 .(-12) = -12
-1 . 12 = -12
6 . (-2) = -12
- 6 . 2 = -12
Devemos, dentre essas possibilidades, achar uma que a soma dos números dê 4. Concluímos que 6 +(- 2) = 4, portanto a forma fatorada desse trinômio será:
(x + 6) (x – 2)
Esse caso de fatoração só pode ser utilizado em expressões algébricas que possuem dois monômios e os mesmos devem estar elevados ao quadrado (elevados à quinta potência).
Chegamos à conclusão que a diferença de dois quadrados pode ser utilizada, quando:
-Tivermos uma expressão algébrica com dois monômios (sejam binômios).
- Os dois monômios forem quadrados.
- A operação entre eles for de subtração.
Veja alguns exemplos de expressões algébricas que seguem esse modelo:
• a2 - 16
• 1 – a2
3
• 4x2 – b2
Como fazer essa fatoração
Dada a expressão algébrica 9x2 – 81, veja os passos que devemos tomar para chegarmos à forma fatorada utilizando o 5º caso de fatoração.
A forma fatorada será (3x – 9) (3x + 9).
Veja alguns exemplos:
Exemplo 1:
A expressão algébrica x2 – 4 é uma expressão com dois monômios e as raízes quadradas são respectivamente x e 2, então a sua forma fatorada é (x – 2) (x + 2).
Exemplo 2:
Dada a expressão algébrica 16x2 – 25, a raiz dos termos 16x2 e 25 é respectivamente 4x e 5. Então, a forma fatorada é (4x – 5) (4x + 5).
Exemplo 3:
Dada a expressão algébrica 36x2 – 81y2, a raiz dos termos 36x2 e 81y2 é respectivamente 6x e 9y. Então, a forma fatorada é (6x – 9y) (6x + 9y).
Fonte mundoeducacao.com.br
segunda-feira, 2 de dezembro de 2019
Taxonomia Como funciona o sistema de classificação dos seres vivos
Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
www.youtube.com/accbarroso1 O gorila também pertence à família dos hominidae como os seres humanos
Imagine todos os seres vivos do planeta, tanto animais como vegetais. Agora, tente pensar em uma denominação para cada um deles, de forma que seus nomes os agrupe conforme suas características em comum. Difícil, não é? Mas é exatamente isso que um ramo da biologia faz. Existem pessoas que trabalham apenas para identificar e nomear espécies - os botânicos (no caso das plantas) e os zoólogos (no caso dos animais) e são chamados sistematas.
É muito importante para a ciência que todos os seres vivos sejam identificados, ou não seria possível estudá-los. A ciência agrupa os seres vivos conforme as características que eles apresentam em comum. Como num jogo de encaixar, cada grupo possui um subgrupo, o qual possui outro subgrupo, e a cada divisão as similaridades ficam cada vez mais acentuadas.
Por exemplo, no reino animal estão todos os animais. Nele, há diversos subgrupos que unem os animais que têm mais coisas em comum, como o dos mamíferos, que engloba apenas animais que mamam. A partir daí, há mais subgrupos, como os que são gerados em placenta (placentários) e que são a maioria, ou os que colocam ovos - esse é o caso dos ornitorrincos.
Ordem decrescente
A classificação básica dos seres vivos é, em ordem decrescente: reino, filo, classe, ordem, família, gênero, e espécie. Em muitos casos, há tantas especializações que esta classificação não é suficiente. Por isso foram criadas algumas subdivisões dentro de ordem, classe, e espécie. No caso do grupo "classe", encontra-se a superclasse (que fica um grau acima da classe) e a infraclasse (que fica um grau abaixo da classe). Da mesma maneira ocorre com o grupo da ordem: existie a superordem e a infraordem. No grupo de espécies, encontra-se a subespécie.
Essas subdivisões são muito comuns no caso dos insetos. A razão disso, está muitas vezes ligada à peculiaridades como número de articulações nas antenas - é o caso de uma espécie de besouro. Estudiosos descobriram que uma espécie de besouro tem alguns indivíduos com número maior de articulações nas antenas. E estes apenas se reproduziam com os seus iguais. Então, esses besouros foram classificados em uma subespécie.
O mesmo acontece com os cães. Geneticamente, são idênticos aos lobos (Cannis lupus). Mas apresentam diversas diferenças quanto a tamanho e forma. Assim, são classificados como uma subespécie dos lobos: são os Cannis (gênero) lupus (espécie) familiaris (subespécie).
Ao usar o ser humano como exemplo, veja uma classificação taxonômica completa:
# Reino: Animalia (o homem é um animal, e nesse grupo estão todos os animais).
# Filo: Chordata (possui notocorda - formação da coluna vertebral - no seu desenvolvimento embrionário, e aqui estão todos os vertebrados).
# Classe: Mammalia (seu filhos mamam, e nessa classe estão todos os mamíferos)
# Infraclasse: Placentalia (é um mamífero cuja fêmea possui placenta - mamíferos que não possuem placenta pertencem a outra infraclasse)
# Ordem: Primata
# Família: Hominidae (dentro desse grupo estão as subfamílias Gorilla (gorilas), Pan (chimpanzés), Ardipithecus (extinto), Australopithecus (extinto) , Pierolapithecus (extinto), Sahelanthropus (extinto), Paranthropus (extinto), Kenyanthropus (extinto), Orrorin (extinto), Homininae (seres humanos).
# Subfamília: Homininae
# Gênero: Homo.
Na verdade, o gênero Homo contém diversas espécies, porém, com exceção do sapiens, todas estão extintas. São elas : Homo antecessor, Homo rhodesiensis, Homo rudolfensis, Homo habilis, Homo cepranensis, Homo ergaster, Homo erectus, Homo floresiensis, Homo georgicus, Homo heidelbergensis, Homo neanderthalensis, Homo sapiens.
# Espécie: Homo sapiens.
Conforme os grupos se subdividem de acordo com as características compartilhadas, o número de animais enquadrados diminui. Ao mesmo tempo, estes apresentam cada vez mais características em comum.
Cada grupo de classificação é chamado de táxon - de onde vem o nome taxonomia. Esse sistema de classificação permite que os seres vivos sejam agrupados conforme o seu grau de parentesco e permite compreender melhor a evolução da vida na Terra.
Mariana Aprile é estudante de biologia na Universidade Mackenzie e bolsista do CNPq.
Ângulos no circulo ou circunfêrencia
Professor de Matemática Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves www.accbarrosogestar.wordpress.com
email accbarroso@hotmail.com
extraído do www.mundoeducacao.com.br
A relação entre ângulos e círculo é muito importante no estudo da geometria. Diversos assuntos ligados à astronomia possuem relações estreitas com ângulos no círculo ou na circunferência. Podemos ter ângulos com vértice no centro, no interior ou no exterior de um círculo, cada um apresentando características e propriedades diferentes. Vejamos cada um desses casos:1. Ângulo com vértice no centro da circunferência – Ângulo central.
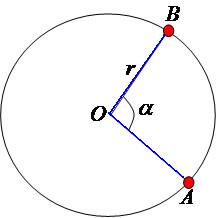
Propriedade: o ângulo central apresenta a mesma medida do arco formado por seus lados, ou seja:
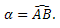
2. Ângulo cujo vértice é um ponto da circunferência – Ângulo Inscrito.
Propriedade: a medida do ângulo inscrito equivale à metade da medida do arco formado por seus lados, ou seja:
Exemplo: Determine o valor de α sabendo que o arco AB mede 60o.
Exemplo: Determine o valor de α sabendo que o arco AB mede 60o.
Solução:
3. Ângulo com vértice exterior à circunferência – Ângulo excêntrico externo.
3. Ângulo com vértice exterior à circunferência – Ângulo excêntrico externo.
Propriedade: o ângulo α equivale à metade da diferença entre as medidas dos arcos formados pelos seus lados, ou seja:
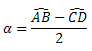
Exemplo: Determine o valor de α na figura abaixo.
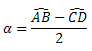
Exemplo: Determine o valor de α na figura abaixo.
4. Ângulo com vértice no interior da circunferência – Ângulo excêntrico interno.
Propriedade: o ângulo excêntrico interno possui medida igual à metade da soma dos arcos formados pelos seus lados, ou seja:
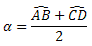
Exemplo: Determine o valor de α na figura abaixo.
Solução:
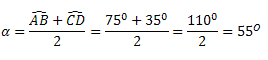
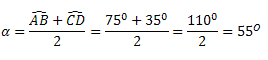
Equação fundamental da reta
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Toda reta não-vertical (reta que possui inclinação diferente de 90º) possui uma equação que representa todos os seus pontos. Essa equação é demonstrada através de um ponto pertencente a essa reta mais o seu coeficiente angular (m).
Considere uma reta s não vertical que passa pelo ponto B (x0, y0) de coeficiente igual a m.
O outro ponto A(x,y), pertencente ao plano cartesiano, irá pertencer a reta s se o cálculo do coeficiente angular (m) da reta s for igual:
m = ∆y = y – y0
∆x x – x0
Podemos representar essa igualdade da seguinte forma:
m = y – y0
x – x0
y – y0 = m (x – x0)
Essa equação formada é chamada de equação fundamental da reta.
Dessa forma podemos concluir que a equação fundamental da reta é obtida por um ponto pertencente a essa reta mais o seu coeficiente angular, ficando sempre em função de outro ponto.
Exemplo 1:
Determine a equação fundamental da reta que passa pelo P(1/4,-3,2) de coeficiente angular m = -1/2.
Os dados oferecidos no enunciado são:
P(x0, y0) = (1/4,-3,2)
m = -1/2
Substituindo-os na equação fundamental da reta temos:
y – y0 = m (x – x0)
y – (-3/2) = -1/2 (x – 1/4)
y + 3/2 = -1/2 (x – 1/4)
2(y + 3/2) = -x + 1/4
2y + 3 = -x + 1/4
8y + 12 = -4x + 1 4 4
4x + 8y + 11 = 0
Exemplo 2:
Represente por meio de uma equação a reta que passa por esses dois pontos A(1,8) e B(4,2).
Foi dito na explicação acima que a equação fundamental de uma reta é determinada por um ponto pertencente à reta e o seu coeficiente angular. O ponto foi dado no enunciado, falta calcular o seu coeficiente angular.
m = yB - yA xB – xA
m = 2 – 8 = - 6 = - 2
4 – 1 3
Escolha um dos dois pontos e monte a equação fundamental da reta que passa pelos pontos A e B.
Ponto A (1,8) e m = -2
y – y0 = m (x – x0)
y – 8 = - 2 (x – 1)
y – 8 = - 2x + 2
2x + y – 10 = 0.
Regra de Sarrus
Regra de Sarrus
Marcos Noé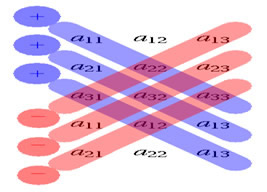
Regra de Sarrus
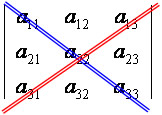
Diagonal principal: a11, a22 e a33.
Diagonal secundária: a13, a22, a31.
A aplicação da Regra de Sarrus consiste em escrever a matriz seguida da repetição de suas duas primeiras colunas. Feito esse processo, verifique a presença de três diagonais principais e três diagonais secundárias.
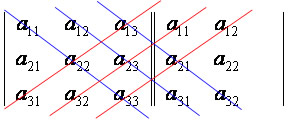
O determinante será calculado por meio da diferença entre o somatório do produto das três diagonais principais e o somatório do produto das três diagonais secundárias. Observe:
Diagonal principal
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} – {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)}
Exemplo 1:
Vamos calcular o valor do determinante da matriz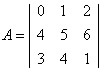
.
Diagonal principal
(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)
Diagonal secundária
(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)
Determinante
D = {(a11 * a22 * a33) + (a12 * a23 * a31) + (a13 * a21 * a32)} – {(a13 * a22 * a31) + (a11 * a23 * a32) + (a12 * a21 * a33)}
Exemplo 1:
Vamos calcular o valor do determinante da matriz
.
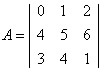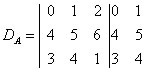
Diagonais principais
0 * 5 * 1 = 0
1 * 6 * 3 = 18
2 * 4 * 4 = 32
0 + 18 + 32 = 50
Diagonais secundárias
2 * 5 * 3 = 30
0 * 6 * 4 = 0
1 * 4 * 1 = 4
30 + 0 + 4 = 34
Determinante
DA = 50 – 34
DA = 16
Exemplo 2:
Dada a matriz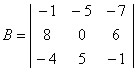
, calcule o seu determinante.
Diagonais principais
(–1) * 0 * (–1) = 0
(–5) * 6 * (–4) = 120
(–7) * (8) * (5) = – 280
0 + 120 + (–280)
120 – 280
– 160
Diagonais secundárias
(–7) * 0 * (–4) = 0
(–1) * 6 * 5 = – 30
(–5) * 8 * (–1) = 40
0 + (–30) + 40
–30 +40
10
Determinante
DB = –160 – 10
DB = – 170
0 * 5 * 1 = 0
1 * 6 * 3 = 18
2 * 4 * 4 = 32
0 + 18 + 32 = 50
Diagonais secundárias
2 * 5 * 3 = 30
0 * 6 * 4 = 0
1 * 4 * 1 = 4
30 + 0 + 4 = 34
Determinante
DA = 50 – 34
DA = 16
Exemplo 2:
Dada a matriz
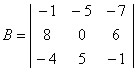, calcule o seu determinante.Diagonais principais
(–1) * 0 * (–1) = 0
(–5) * 6 * (–4) = 120
(–7) * (8) * (5) = – 280
0 + 120 + (–280)
120 – 280
– 160
Diagonais secundárias
(–7) * 0 * (–4) = 0
(–1) * 6 * 5 = – 30
(–5) * 8 * (–1) = 40
0 + (–30) + 40
–30 +40
10
Determinante
DB = –160 – 10
DB = – 170
Assinar:
Postagens (Atom)