Equações do 1º grau com uma variável
Equação é toda sentença matemática aberta representada por uma igualdade, em que exista uma ou mais letras que representam números desconhecidos.
Exemplo:X + 3 = 12 – 4
Forma geral: ax = b, em que x representa a variável (incógnita) e a e b são números racionais, com a 0. Dizemos que a e b são os coeficientes da equação.(ax = b, é a forma mais simples da equação do 1º grau)
Exemplos:
x - 4 = 2 + 7, (variável x)
2m + 6 = 12 – 3 ,(variável m)
-2r + 3 = 31, (variável r)
5t + 3 = 2t – 1 , (variável t)
3(b – 2) = 3 + b,(variável b)
4 + 7 = 11, (é uma igualdade, mas não possui uma variável, portanto não é uma equação do 1º grau)
3x – 12 > 13, (possui uma variável, mas não é uma igualdade, portanto não é uma equação do 1º grau)
Obs:
Devemos observar duas partes em uma equação, o 1º membro à esquerda do sinal de igual e o 2º membro à direita do sinal de igual.
Veja:
Conjunto Universo:Conjunto formado por todos os valores que a variável pode assumir. Representamos pela letra U.
Conjunto Solução:Conjunto formado por valores do conjunto U que tornam a sentença verdadeira. Representamos pela letra S.
Exemplo:
Dentre os elementos do conjunto F = {0, 2, 3, 6, 8, 9}, qual deles torna a sentença matemática
2x – 4 = 2, verdadeira.
2(0) – 4 = 2 Errado
2(2) – 4 = 2 Errado
2(3) – 4 = 2 Verdadeiro
2(6) – 4 = 2 Errado
2(8) – 4 = 2 Errado
2(9) – 4 = 2 Errado
Devemos observar que o conjunto U = {0, 2, 3, 6, 8, 9}, e conjunto S = {3}
Sistemas de Equações do 1º Grau
SISTEMA COM DUAS EQUAÇÕES DO 1º GRAU COM DUAS VARIÁVEIS
Resolver um sistema de duas equações do 1º grau com duas variáveis, x e y, por exemplo, significa determinar o único par ordenado (x,y) que é a solução do sistema. Podemos encontrar a solução de um sistema usando os métodos da adição, substituição e comparação.
Exercícios Resolvidos:
1) Um número mais a sua metade é igual a 150. Qual é esse número?
Solução:
n + n/2 = 150
2n/2 + n/2 = 300/2
2n + n = 300
3n = 300
n = 300/3
n = 100
Resposta: Esse número é 100.
2) A diferença entre um número e sua quinta parte é igual a 36. Qual é esse número?
Solução:
x - x/5 = 36
(5 x - x)/5 = 36
4x /5 = 36
4x = 36.5
4x = 180
x = 180/4
x = 45
Resposta: Esse número é 45.
3) O triplo de um número é igual a sua metade mais 20. Qual é esse número?
Solução:
3 m = m/2 + 20
6m/2 = (m+40)/2
6m = m + 40
6m - m =
5m = 40
m = 40/5
m = 8
Resposta: Esse número é 8.
4) O triplo de um número, mais 5, é igual a 254. Qual é esse número?
Solução:
3p + 5 = 254
3p = 254 - 5
3p = 249
p = 249/3
p = 83
Resposta: Esse número é 83.
5) O quádruplo de um número, diminuído de três, é igual a 99. Qual é esse número ?
6) Júlio tem 15 anos e Eva tem 17 anos. Daqui a quantos anos a soma de suas idades será 72 anos?
7) Num pátio há bicicletas e carros num total de 20 veículos e 56 rodas. Determine o número de bicicletas e de carros.
8) A metade dos objetos de uma caixa mais a terça parte desses objetos é igual a 75. Quantos objetos há na caixa?
9) Em uma fábrica, um terço dos empregados são estrangeiros e 90 empregados são brasileiros. Quantos são os empregados da fábrica?
10) Numa caixa, o número de bolas pretas é o triplo de bolas brancas. Se tirarmos 4 brancas e 24 pretas, o número de bolas de cada cor ficará igual. Qual a quantidade de bolas brancas?
11) Como devo distribuir R$ 438,00 entre três pessoas, de modo que as duas primeiras recebam quantias iguais e a terceira receba o dobro do que receber as duas primeiras?
12) Ao triplo de um número foi adicionado 40. O resultado é igual ao quíntuplo do número. Qual é esse número?
Gráfico de uma equação de 1º grau com duas variáveis
Sabemos que uma equação do 1º grau com duas variáveis possui infinitas soluções.
Cada uma dessas soluções pode ser representada por um par ordenado (x, y).
quinta-feira, 2 de julho de 2020
Matrizes e determinantes
Matrizes formam um importante conceito em matemática, de especial uso no estudo de transformações lineares. Não é o propósito desta página a teoria dessas transformações, mas apenas alguns fundamentos e operações básicas com matrizes que as representam.
Uma matriz Am,n pode ser entendida como um conjunto de mn (m multiplicado por n) números, dispostos em m linhas e n colunas, conforme figura ao lado.
c (A + B) = cA + cB e d (cA) = dc (A).
E, também, se cA = cB então A = B.
c11 = 4.1 + 0.2 + 5.1 = 9 | c12 = 4.2 + 0.5 + 5.0 = 8 |
c21 = 1.1 + 1.2 + 3.1 = 6 | c22 = 1.2 + 1.5 + 3.0 = 7 |
Entretanto, na multiplicação de matrizes, a ordem dos fatores não é indiferente.
Em geral AB ? BA. Se AB = BA, as matrizes são ditas comutativas.
1) Se os produtos A(BC) e (AB)C são possíveis de cálculo, então A(BC) = (AB)C.
2) Se os produtos AC e BC são possíveis, então (A+B)C = AC + BC.
3) Se os produtos CA e CB são possíveis, então C(A+B) = CA + CB.
4) Se Ip é a matriz unitária pp conforme já mencionado, então: Ip Ap,n = Ap,n e Bm,p Ip = Bm,p.
O primeiro passo é acrescentar uma matriz unitária no lado direito de A.
Agora, o objetivo é somar ou subtrair linhas multiplicadas por coeficientes de forma a obter a matriz unitária no lado esquerdo (processo de Gauss-Jordan).
1ª linha = 1ª linha + 2ª linha multiplicada por -1.
2ª linha = 2ª linha + 1ª linha multiplicada por -1.
3ª linha = 3ª linha + 1ª linha multiplicada por -2.
3ª linha = 3ª linha + 2ª linha multiplicada por -3.
3ª linha = 3ª linha multiplicada por -1.
2ª linha = 2ª linha + 3ª linha multiplicada por -1.
E a matriz inversa é a parte da direita.
Veja ao lado para uma matriz A2,2 (determinante de 2ª ordem).
O prefixo det é colocado antes da matriz para indicar determinante. Ou, de forma mais compacta, os colchetes na matriz são substituídos por barras verticais para o mesmo efeito.
Se o índice da coluna for par, o sinal da parcela será negativo e positivo do contrário. Para cada determinante restante, o processo é repetido até chegar a determinantes de 2ª ordem, que são calculados pela fórmula anterior.
A figura acima demonstra o método para um determinante de terceira ordem.
1) Mantidas as ordens dos elementos, um determinante não se altera se linhas e colunas são trocadas.
2) Se duas linhas ou duas colunas são trocadas entre si, o determinante muda de sinal.
3) Se os elementos de duas linhas ou colunas são iguais entre si, proporcionais entre si ou nulos, o determinante é nulo (k é um número qualquer).
4) Se os elementos de uma mesma linha ou coluna têm um fator de multiplicação comum, ele pode ser colocado em evidência.
5) Um determinante não se altera se aos elementos de uma linha ou coluna são somados ou subtraídos os elementos (ou múltiplos deles) de outra linha ou coluna.
Seja o sistema de equações lineares ao lado e o determinante B calculado pelos coeficientes das variáveis.
E os determinantes conforme figura a lado.
Então a solução é dada por: x = B1/B, y = B2/B e z = B3/B.
Portanto, na matriz abaixo, de 2 linhas e 3 colunas, temos:
Adição e subtração
Esta operação só pode ser feita com matrizes de mesmo número de linhas e mesmo número de colunas.Multiplicação por um escalar
Algumas propriedades das operações anteriores
Sejam A e B matrizes m,n e c e d escalares. Então:c (A + B) = cA + cB e d (cA) = dc (A).
E, também, se cA = cB então A = B.
Matrizes nulas e unitárias
Multiplicação de matrizes
Sejam as matrizes Am,p e Bp,n (o número de colunas da primeira deve ser igual ao número de linhas da segunda). O produto AB é dado pela matriz Cm,n cujos elementos são calculados por:c21 = 1.1 + 1.2 + 3.1 = 6 | c22 = 1.2 + 1.5 + 3.0 = 7 |
Temos então a fórmula genérica:
Ordem dos fatores
Se A e B são matrizes quadradas (igual número de linhas e colunas), ambos os produtos AB e BA podem ser calculados.Em geral AB ? BA. Se AB = BA, as matrizes são ditas comutativas.
Algumas propriedades do produto de matrizes
Sejam as matrizes A, B e C.1) Se os produtos A(BC) e (AB)C são possíveis de cálculo, então A(BC) = (AB)C.
2) Se os produtos AC e BC são possíveis, então (A+B)C = AC + BC.
3) Se os produtos CA e CB são possíveis, então C(A+B) = CA + CB.
4) Se Ip é a matriz unitária pp conforme já mencionado, então: Ip Ap,n = Ap,n e Bm,p Ip = Bm,p.
Matriz inversa
Sejam as matrizes quadradas An,n e Bn,n. Se BA = In , onde In é a matriz unitária conforme já visto, então B é chamada de matriz inversa esquerda de A.Para achar a matriz inversa:
Por exemplo, seja a matriz A ao lado e desejamos saber sua inversa esquerda B.O primeiro passo é acrescentar uma matriz unitária no lado direito de A.
Agora, o objetivo é somar ou subtrair linhas multiplicadas por coeficientes de forma a obter a matriz unitária no lado esquerdo (processo de Gauss-Jordan).
1ª linha = 1ª linha + 2ª linha multiplicada por -1.
2ª linha = 2ª linha + 1ª linha multiplicada por -1.
3ª linha = 3ª linha + 1ª linha multiplicada por -2.
3ª linha = 3ª linha + 2ª linha multiplicada por -3.
3ª linha = 3ª linha multiplicada por -1.
2ª linha = 2ª linha + 3ª linha multiplicada por -1.
E a matriz inversa é a parte da direita.
Determinantes de 2ª ordem
O conceito de determinante está ligado ao de matriz, embora seja completamente distinto: enquanto matriz é o conjunto de elementos conforme já mencionado, determinante é o resultado de uma operação aritmética com os elementos de uma matriz, que obedece a uma determinada regra. Só se aplica a matrizes quadradas.O prefixo det é colocado antes da matriz para indicar determinante. Ou, de forma mais compacta, os colchetes na matriz são substituídos por barras verticais para o mesmo efeito.
Determinantes de ordens superiores
Para determinantes de 3ª ordem ou superior, o cálculo pode ser feito pela decomposição: considera-se, por exemplo, a primeira linha da matriz e somam-se as parcelas de cada elemento desta linha multiplicado pelo determinante da matriz que restar pela eliminação da linha e coluna que passam pelo elemento.A figura acima demonstra o método para um determinante de terceira ordem.
Algumas propriedades dos determinantes
1) Mantidas as ordens dos elementos, um determinante não se altera se linhas e colunas são trocadas.
2) Se duas linhas ou duas colunas são trocadas entre si, o determinante muda de sinal.
3) Se os elementos de duas linhas ou colunas são iguais entre si, proporcionais entre si ou nulos, o determinante é nulo (k é um número qualquer).
4) Se os elementos de uma mesma linha ou coluna têm um fator de multiplicação comum, ele pode ser colocado em evidência.
5) Um determinante não se altera se aos elementos de uma linha ou coluna são somados ou subtraídos os elementos (ou múltiplos deles) de outra linha ou coluna.
Exemplo de aplicação de determinantes
Seja o sistema de equações lineares ao lado e o determinante B calculado pelos coeficientes das variáveis.
E os determinantes conforme figura a lado.
Então a solução é dada por: x = B1/B, y = B2/B e z = B3/B.
Fonte: www.mspc.eng.br
Distribuição Eletrônica Linus Pauling e as camadas eletrônicas do átomo
Um problema para os químicos era construir uma teoria consistente que explicasse como os elétrons se distribuíam ao redor dos átomos, dando-lhes as características de reação observadas em nível macroscópico.
Foi o cientista americano Linus C. Pauling quem apresentou a teoria até o momento mais aceita para a distribuição eletrônica.
Sobre Pauling, é sempre interessante citar que ele foi duas vezes laureado com o Prêmio Nobel. O de química em 1954, por suas descobertas sobre as ligações atômicas, e o da Paz em 1962, por sua militância contra as armas nucleares.
Para entender a proposta de Pauling, é preciso primeiro dar uma olhadinha no conceito de camadas eletrônicas, o princípio que rege a distribuição dos elétrons em torno do átomo em sete camadas, identificadas pelas letras K, L, M, N, O, P e Q.
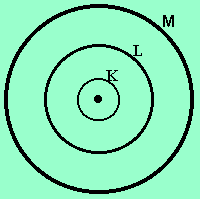
Uma característica destas camadas é que cada uma delas possui um número máximo de elétrons que podem comportar, conforme tabela que segue:
Camada
Número máximo de elétrons
K
2
L
8
M
18
N
32
O
32
P
18
Q
8
Pauling apresentou esta distribuição dividida em níveis e subníveis de energia, em que os níveis são as camadas e os subníveis divisões destes (representados pelas letras s, p, d, f), possuindo cada um destes subníveis também um número máximo de elétrons.
Subnível
Número máximo de elétrons
Nomenclatura
s
2
s2
p
6
p6
d
10
d10
f
14
f14
Quando combinados níveis e subníveis, a tabela de distribuição eletrônica assume a seguinte configuração:
Camada
Nível
Subnível
Total de elétrons
s2
p6
d10
f14
K
1
1s
2
L
2
2s
2p
8
M
3
3s
3p
3d
18
N
4
4s
4p
4d
4f
32
O
5
5s
5p
5d
5f
32
P
6
6s
6p
6d
18
Q
7
7s
7p
8
A distribuição eletrônica, conforme Pauling, não era apenas uma ocupação pelos elétrons dos espaços vazios nas camadas da eletrosfera.
Os elétrons se distribuem segundo o nível de energia de cada subnível, numa seqüência crescente em que ocupam primeiro os subníveis de menor energia e, por último, os de maior.
É esta a tradução do diagrama de energia de Pauling, que define esta ordem energética crescente que é também a seqüência de distribuição dos elétrons
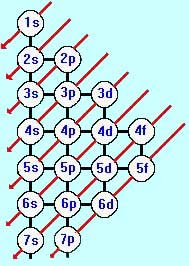
Diagrama de Linus Pauling
Na figura, as setas indicam a ordem crescente dos níveis de energia: 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14 5d10 6p6 7s2 5f14 6d10
Note que como a energia de 4s2 é menor, esta posição vem antes de 3p6 e 3d10.
Assim, seguindo o diagrama de Pauling, podemos montar a distribuição eletrônica de qualquer elemento químico, como por exemplo:
Elemento químico Número atômico Distribuição eletrônica
He Hélio 2 1s2
K = 2
Cl Cloro 17 1s2 2s2 2p6 3s2 3p5
K = 2, L = 8, M = 7
Zr Zircônio 40 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d2
K = 2, L = 8, M = 18, n = 10, O =2
Pt Platina 78 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s1 4f14 5d9
K = 2, L = 8, M = 18, N = 32, O = 16, P = 2
Lembre-se que a soma da distribuição dos elétrons, tanto nos subníveis quanto nas camadas deve bater com o número atômico, como no exemplo da Platina:
Camada
Nível
Distribuição eletrônica da platina
Total de elétrons
s2
p6
d10
f14
K
1
1s2
2
L
2
2s2
2p6
8
M
3
3s2
3p6
3d10
18
N
4
4s2
4p6
4d10
4f14
32
O
5
5s2
5p6
5d8
16
P
6
6s2
-
2
Q
7
-
-
Total
78
Algumas edições da Tabela Periódica informam também a distribuição eletrônica dos elementos químicos, o que facilita muito o trabalho de quem precisa operar estes dados.
Mas, independentemente disto, é muito importante conhecer os mecanismos que regem esta distribuição, e particularmente o conceito de níveis e subníveis de energia, ponto de partida para estudos mais avançados como os princípios da mecânica quântica.
*Carlos Roberto de Lana é engenheiro químico e professor.
Foi o cientista americano Linus C. Pauling quem apresentou a teoria até o momento mais aceita para a distribuição eletrônica.
Sobre Pauling, é sempre interessante citar que ele foi duas vezes laureado com o Prêmio Nobel. O de química em 1954, por suas descobertas sobre as ligações atômicas, e o da Paz em 1962, por sua militância contra as armas nucleares.
Para entender a proposta de Pauling, é preciso primeiro dar uma olhadinha no conceito de camadas eletrônicas, o princípio que rege a distribuição dos elétrons em torno do átomo em sete camadas, identificadas pelas letras K, L, M, N, O, P e Q.
Uma característica destas camadas é que cada uma delas possui um número máximo de elétrons que podem comportar, conforme tabela que segue:
Camada
Número máximo de elétrons
K
2
L
8
M
18
N
32
O
32
P
18
Q
8
Pauling apresentou esta distribuição dividida em níveis e subníveis de energia, em que os níveis são as camadas e os subníveis divisões destes (representados pelas letras s, p, d, f), possuindo cada um destes subníveis também um número máximo de elétrons.
Subnível
Número máximo de elétrons
Nomenclatura
s
2
s2
p
6
p6
d
10
d10
f
14
f14
Quando combinados níveis e subníveis, a tabela de distribuição eletrônica assume a seguinte configuração:
Camada
Nível
Subnível
Total de elétrons
s2
p6
d10
f14
K
1
1s
2
L
2
2s
2p
8
M
3
3s
3p
3d
18
N
4
4s
4p
4d
4f
32
O
5
5s
5p
5d
5f
32
P
6
6s
6p
6d
18
Q
7
7s
7p
8
A distribuição eletrônica, conforme Pauling, não era apenas uma ocupação pelos elétrons dos espaços vazios nas camadas da eletrosfera.
Os elétrons se distribuem segundo o nível de energia de cada subnível, numa seqüência crescente em que ocupam primeiro os subníveis de menor energia e, por último, os de maior.
É esta a tradução do diagrama de energia de Pauling, que define esta ordem energética crescente que é também a seqüência de distribuição dos elétrons
Diagrama de Linus Pauling
Na figura, as setas indicam a ordem crescente dos níveis de energia: 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s2 4f14 5d10 6p6 7s2 5f14 6d10
Note que como a energia de 4s2 é menor, esta posição vem antes de 3p6 e 3d10.
Assim, seguindo o diagrama de Pauling, podemos montar a distribuição eletrônica de qualquer elemento químico, como por exemplo:
Elemento químico Número atômico Distribuição eletrônica
He Hélio 2 1s2
K = 2
Cl Cloro 17 1s2 2s2 2p6 3s2 3p5
K = 2, L = 8, M = 7
Zr Zircônio 40 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d2
K = 2, L = 8, M = 18, n = 10, O =2
Pt Platina 78 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 5s2 4d10 5p6 6s1 4f14 5d9
K = 2, L = 8, M = 18, N = 32, O = 16, P = 2
Lembre-se que a soma da distribuição dos elétrons, tanto nos subníveis quanto nas camadas deve bater com o número atômico, como no exemplo da Platina:
Camada
Nível
Distribuição eletrônica da platina
Total de elétrons
s2
p6
d10
f14
K
1
1s2
2
L
2
2s2
2p6
8
M
3
3s2
3p6
3d10
18
N
4
4s2
4p6
4d10
4f14
32
O
5
5s2
5p6
5d8
16
P
6
6s2
-
2
Q
7
-
-
Total
78
Algumas edições da Tabela Periódica informam também a distribuição eletrônica dos elementos químicos, o que facilita muito o trabalho de quem precisa operar estes dados.
Mas, independentemente disto, é muito importante conhecer os mecanismos que regem esta distribuição, e particularmente o conceito de níveis e subníveis de energia, ponto de partida para estudos mais avançados como os princípios da mecânica quântica.
*Carlos Roberto de Lana é engenheiro químico e professor.
Média Geométrica
Para calcularmos a média geométrica entre números
devemos realizar a multiplicação entre eles e, logo em seguida, extrair a
raiz com índice igual ao número de fatores utilizados na multiplicação.
Por exemplo, ao calcular a média geométrica dos números 2, 4 e 6,
efetuamos o seguinte cálculo:
A média geométrica é muito utilizada nas situações
envolvendo aumentos sucessivos. Por exemplo, vamos considerar um aumento
de salário sucessivo de 15% no primeiro mês, 12% no segundo mês e 21%
no terceiro mês.
Vamos determinar a média geométrica dos aumentos, mas para isso as taxas percentuais devem ser transformadas em taxa unitárias, observe:
15% = 1,15
12% = 1,12
21% = 1,21
O valor 1,1594 corresponde a taxa média de 15,94% de todos os aumentos sucessivos. Isso indica que se aplicarmos três vezes consecutivas a taxa de 15,94% corresponderá ao aumento sucessivo dos percentuais de 15%, 12% e 21%.
Suponhamos que o salário reajustado seja de R$ 600,00. Acompanhe os aumentos utilizando as duas opções de reajustes:
1ª opção
600,00 + 15% = 690,00
690,00 + 12% = 772,80
772,80 + 21% = 935,09
2ª opção
600,00 + 15,94% = 695,64
695,64 + 15,94% = 806,53
806,53 + 15,94% = 935,09
Vamos determinar a média geométrica dos aumentos, mas para isso as taxas percentuais devem ser transformadas em taxa unitárias, observe:
15% = 1,15
12% = 1,12
21% = 1,21
O valor 1,1594 corresponde a taxa média de 15,94% de todos os aumentos sucessivos. Isso indica que se aplicarmos três vezes consecutivas a taxa de 15,94% corresponderá ao aumento sucessivo dos percentuais de 15%, 12% e 21%.
Suponhamos que o salário reajustado seja de R$ 600,00. Acompanhe os aumentos utilizando as duas opções de reajustes:
1ª opção
600,00 + 15% = 690,00
690,00 + 12% = 772,80
772,80 + 21% = 935,09
2ª opção
600,00 + 15,94% = 695,64
695,64 + 15,94% = 806,53
806,53 + 15,94% = 935,09
Por Marcos Noé
Graduado em Matemática
Graduado em Matemática
sistema binário
O sistema binário de computação já era conhecido na China uns 3000 a.C., de acordo com os manuscritos da época. Quarenta e seis séculos depois, Leibniz redescobre o sistema binário.
Este sistema de numeração binário é muito importante, na medida em que, modernamente, é de largo alcance por ser utilizado nas calculadoras electrónicas, computadores e nas estruturas que envolvem relações binárias. Este sistema pode ser chamado sistema de base dois, binário ou dual, o qual utiliza apenas dois algarismos, o 0 e o 1, os quais nas estruturas dessas máquinas se fazem corresponder às situações de sim-não, aberto-fechado, contacto-interrupção, passagem-vedação, etc., uma vez que os circuitos digitais são constituídos por elementos dotados de dois estados distintos.
A cada um dos símbolos do sistema binário chama-se um «bit».
O maior inconveniente da base dois é que a representação de cada número envolve muitos algarismos. Por exemplo, cem mil, que na base dez se representa por 5 algarismos, na base dois representa-se por 17 algarismos! Porém, este inconveniente é superado nas máquinas electrónicas pela velocidade.
Como é que funciona, afinal, este sistema binário?
Na base dois, um número imediatamente à esquerda de outro, representa, em relação a este, um número de unidades duas vezes maior. (..., 2 3, 2 2, 21, 20)
Como é que se representa um número decimal (numeração árabe) na base dois?
Temos então que, para passar da notação binária para a notação decimal, o processo não é muito complexo e é o seguinte, por exemplo:
10011010(2)=1×27+0×26+0×25+1×24+1×23+0×22+1×21+0×20
= 128+0+0+16+8+0+2+0=
=154(10) (O que é uma maneira bem mais prática de representar o mesmo número!)
8(10)= ?(2)
Podemos então concluir que 8(10)=1000(2) ( 8 = 1×2³+ +0×2²+ 0×2¹+0×20)
Vejamos este outro exemplo:
66(10)= ?(2)
Podemos então concluir que 66(10)=1000010(2) ( 66 = 1×26+ + 0×25+0×24+0×23+0×22+1×21+0×20 )
Este sistema de numeração binário é muito importante, na medida em que, modernamente, é de largo alcance por ser utilizado nas calculadoras electrónicas, computadores e nas estruturas que envolvem relações binárias. Este sistema pode ser chamado sistema de base dois, binário ou dual, o qual utiliza apenas dois algarismos, o 0 e o 1, os quais nas estruturas dessas máquinas se fazem corresponder às situações de sim-não, aberto-fechado, contacto-interrupção, passagem-vedação, etc., uma vez que os circuitos digitais são constituídos por elementos dotados de dois estados distintos.
O maior inconveniente da base dois é que a representação de cada número envolve muitos algarismos. Por exemplo, cem mil, que na base dez se representa por 5 algarismos, na base dois representa-se por 17 algarismos! Porém, este inconveniente é superado nas máquinas electrónicas pela velocidade.
Na base dois, um número imediatamente à esquerda de outro, representa, em relação a este, um número de unidades duas vezes maior. (..., 2 3, 2 2, 21, 20)
Como é que se representa um número decimal (numeração árabe) na base dois?
Vejamos os seguintes exemplos:
| Notação decimal | Notação binária |
|---|---|
| 0 | 0 ( =0×20 ) |
| 1 | 1 ( =1×20 ) |
| 2 | 10 ( =1×21+0×20) |
| 3 | 11 ( =1×21+1×20) |
| 4 | 100 ( =1×22+0×21+0×20) |
| 5 | 101 ( =1×22+0×21+1×20) |
| 6 | 110 ( =1×22+1×21+0×20) |
| 7 | 111 ( =1×22+1×21+1×20) |
10011010(2)=1×27+0×26+0×25+1×24+1×23+0×22+1×21+0×20
= 128+0+0+16+8+0+2+0=
=154(10) (O que é uma maneira bem mais prática de representar o mesmo número!)
Como é que se passa da base decimal para a base binária?
Agora o processo é um pouco mais complexo, mas não deixa de ser interessante, vejamos os seguintes exemplos:8(10)= ?(2)
Façamos o seguinte raciocínio:
Vejamos este outro exemplo:
66(10)= ?(2)
Fonte: www.educ.fc.ul.pt
Bioluminescência
Processo bioquímico utilizado por muitos animais e algas marinhas, resultando na produção de luz. O processo é feito através da oxidação de uma proteína chamada Luciferina por uma enzima chamada Luciferase.
A bioluminescência é produzida por componentes do fitoplâncton, principalmente dinoflagelados como a Noctiluca. Esta alga é a responsável pelos pontos de luz azul-esverdeada produzidos na areia das praias e na água, visíveis durante a noite. Muitos invertebrados também produzem luz, principalmente os crustáceos, como os camarões, vermes, equinodermas e lulas. Os peixes são os únicos vertebrados capazes de produzir luz.
A bioluminescência se dá principalmente em órgãos especiais denominados fotóforos, os quais estão presentes em locais específicos do corpo e em quantidades variáveis, dependendo da espécie em questão. Estes órgãos luminosos são formados por um tecido fotogênico, no qual a reação bioquímica se processa, ligado a terminações nervosas que transmitem o comando para a produção de luz.
Em outros casos de bioluminescência, não são os fotóforos que produzem luz, mas bactérias luminescentes aprisionadas em pontos específicos do corpo de algumas espécies de peixes. Como neste caso não há o controle nervoso deste processo, comumente existem membranas que podem cobrir e descobrir o sítio luminoso de acordo com a necessidade do peixe.
O Brasil é o país com a maior diversidade de espécies luminescentes no mundo, entre elas vaga-lumes que produzem os mais belos espetáculos da natureza, como as chamadas larvas ‘trenzinho’, que emitem luz em duas cores. Com a devastação das florestas, no entanto, essa esplêndida riqueza está se perdendo.
A função ecológica da bioluminescência é ainda pouco compreendida, mas já se sabe que em muitos casos está associada a:
- iluminação do campo de visão
- atração de presas através de iscas luminosas
- reconhecimento de diferentes espécies
- reconhecimento de parceiros sexuais
- adaptações contra predação
A bioluminescência é um processo característico em peixes das regiões profundas dos oceanos, onde há a rarefação ou mesmo a ausência total de luz natural.
A bioluminescência é produzida por componentes do fitoplâncton, principalmente dinoflagelados como a Noctiluca. Esta alga é a responsável pelos pontos de luz azul-esverdeada produzidos na areia das praias e na água, visíveis durante a noite. Muitos invertebrados também produzem luz, principalmente os crustáceos, como os camarões, vermes, equinodermas e lulas. Os peixes são os únicos vertebrados capazes de produzir luz.
A bioluminescência se dá principalmente em órgãos especiais denominados fotóforos, os quais estão presentes em locais específicos do corpo e em quantidades variáveis, dependendo da espécie em questão. Estes órgãos luminosos são formados por um tecido fotogênico, no qual a reação bioquímica se processa, ligado a terminações nervosas que transmitem o comando para a produção de luz.
Em outros casos de bioluminescência, não são os fotóforos que produzem luz, mas bactérias luminescentes aprisionadas em pontos específicos do corpo de algumas espécies de peixes. Como neste caso não há o controle nervoso deste processo, comumente existem membranas que podem cobrir e descobrir o sítio luminoso de acordo com a necessidade do peixe.
O Brasil é o país com a maior diversidade de espécies luminescentes no mundo, entre elas vaga-lumes que produzem os mais belos espetáculos da natureza, como as chamadas larvas ‘trenzinho’, que emitem luz em duas cores. Com a devastação das florestas, no entanto, essa esplêndida riqueza está se perdendo. A função ecológica da bioluminescência é ainda pouco compreendida, mas já se sabe que em muitos casos está associada a:
- iluminação do campo de visão
- atração de presas através de iscas luminosas
- reconhecimento de diferentes espécies
- reconhecimento de parceiros sexuais
- adaptações contra predação
A bioluminescência é um processo característico em peixes das regiões profundas dos oceanos, onde há a rarefação ou mesmo a ausência total de luz natural.
quarta-feira, 1 de julho de 2020
segunda-feira, 29 de junho de 2020
EXPRESSÕES NUMÉRICAS
EXPRESSÕES NUMÉRICAS
www.youtube.com/accbarroso1
Para resolver uma expressão numérica, efetuamos as operações obedecendo à seguinte ordem :
1°) Potenciação e radiciação
2°) Multiplicações e divisões
3°) Adições e Subtrações
EXEMPLOS
1) 5 + 3² x 2 =
= 5 + 9 x 2 =
= 5 + 18 =
= 23
2) 7² - 4 x 2 + 3 =
= 49 – 8 + 3 =
= 41 + 3 =
= 44
Há expressões onde aparecem os sinais de associação e que devem ser eliminados nesta ordem:
1°) parênteses ( )
2°) colchetes [ ]
3°) chaves { }
exemplos
1°) 40 – [5² + ( 2³ - 7 )] =
= 40 – [5² + ( 8 - 7 )]
= 40 – [25 + 1 ]=
= 40 – 26 =
= 14
2°) 50 –{ 15 + [ 4² : ( 10 – 2 ) + 5 x 2 ] } =
= 50 –{ 15 + [ 16 : 8 + 10 ]}=
= 50 – { 15 + [ 2 + 10 ] } =
= 50 – { 15 +12 } =
= 50 – 27 =
= 23
3°) exemplo
(-3)² - 4 - (-1) + 5²
9 – 4 + 1 + 25
5 + 1 + 25
6 + 25
31
4°) exemplo
15 + (-4) . (+3) -10
15 – 12 – 10
3 – 10
-7
5°) exemplo
5² + √9 – [(+20) : (-4) + 3]
25 + 3 – [ (-5) +3 ]
25 + 3 - [ -2]
25 +3 +2
28 + 2
30
EXPRESSÕES ALGÉBRICAS
São expressões matemáticas que apresentam letras e podem conter números. São também denominadas expressões literais.
Exemplos
- A = 2a + 7b
- B = (3c + 4) - 5
- C = 23c + 4
As letras nas expressões são chamadas variáveis o que significa que o valor de cada letra pode ser substituída por um valor numérico.
PRIORIDADE DAS OPERAÇÕES NUMA EXPRESSÃO ALGÉBRICA
Nas operações em uma expressão algébrica, devemos obedecer a seguinte ordem:
1. Potenciação ou Radiciação
2. Multiplicação ou Divisão
3. Adição ou Subtração
Observações:
Antes de cada uma das três operações citadas anteriormente, deve-se realizar a operação que estiver dentro dos parênteses, colchetes ou chaves.
A multiplicação pode ser indicada por x ou por um ponto . ou às vezes sem sinal, desde que fique clara a intenção da expressão.
Muitas vezes devemos utilizar parênteses quando substituímos variáveis por valores negativos.
EXERCICIOS
1) Calcule o valor das expressões:
a) 7² - 4 = (R:45)
b) 2³ + 10 = (R:18)
c) 5² - 6 = (R:19)
d) 4² + 7⁰= (R:17)
e) 5⁰+ 5³= (R:126)
f) 2³+ 2⁴ = (R:24)
g) 10³ - 10² = (R:900)
h) 80¹ + 1⁸⁰ = (R:81)
i) 5² - 3² = (R:16)
j) 1⁸⁰ + 0⁷⁰ = (R:1)
2) Calcule
a) 3² + 5 = (R:14)
b) 3 + 5² = (R:28)
c) 3² + 5² = (R:34)
d) 5² - 3² = (R:16)
e) 18 - 7⁰ = (R:17)
f) 5³ - 2² = (R:121)
g) 10 + 10² = (R:110)
h) 10³ - 10² = (R:900)
i) 10³ - 1¹ = (R:999)
3) Calcule o valor das expressões
a) 2³ x 5 + 3² = (R:49)b) 70⁰+ 0⁷⁰ - 1 = (R:0)
c) 3 x 7¹ - 4 x 5⁰ = (R:17)d) 3⁴- 2⁴: 8 – 3 x 4 = (R:67)
e) 5² + 3 x 2 – 4 = (R:27)
f) 5 x 2² + 3 – 8 = (R:15)
g) 5² - 3 x 2² - 1 = (R:12)
h) 16 : 2 – 1 + 7² = (R:56)
4) calcule o valor das expressões:
a) 5² : ( 5 +1 -1)+ 4 x 2 = (R:13)
b) (3 +1)² +2 x 5 - 10⁰ = (R:25)
c) c) 3²: ( 4 – 1) + 3 x 2² = (R:15)
d) 70 –[ 5 x (2² : 4) + 3²] = (R:56)
e) ( 7 + 4) x ( 3² - 2³) = (R:11)
f) 5² + 2³ - 2 x (3 + 9) = (R:9)
g) 6² : 3² + 4 x 10 – 12 = (R:32)
h) (7² - 1 ) : 3 + 2 x 5 = (R:26)
5) calcule o valor das expressões:
a) 5 + 4²- 1 = (R:20)
b) 3⁴ - 6 + 2³ = (R:83)
c) 2⁵ - 3² + 1⁹ = (R:24)
d) 10²- 3² + 5 = (R:96)
e) 11² - 3² + 5 = (R:117)
f) 5 x 3² x 4 = (R:180)
g) 5 x 2³ + 4² = (R:56)
h) 5³ x 2² - 12 = (R:488)
6) Calcule o valor das expressões:
a) ( 4 + 3)² - 1 = (R:48)
b) ( 5 + 1 )² + 10 = (R:46)
c) ( 9 – 7 )³ x 8 = (R:64)
d) ( 7² - 5²) + ( 5² - 3 ) = (R:46)
e) 6² : 2 - 1⁴ x 5 = (R:13)
f) 3² x 2³ + 2² x 5² = (R:172)
7) Calcule o valor das expressões:
a) 4²- 10 + (2³ - 5) = (R:9)
b) 30 – (2 + 1)²+ 2³ = (R:29)
c) 30 + [6² : ( 5 – 3) + 1 ] = (R:49)
d) 20 – [6 – 4 x( 10 - 3²) + 1] = (R:17)
e) 50 + [ 3³ : ( 1 + 2) + 4 x 3] = (R:71)
f) 100 –[ 5² : (10 – 5 ) + 2⁴ x 1 ] = (R:79)
g) [ 4² + ( 5 – 3)³] : ( 9 – 7)³ = (R:3)
h) 7²+ 2 x[(3 + 1)² - 4 x 1³] = (R:73)
i) 25 + { 3³ : 9 +[ 3² x 5 – 3 x (2³- 5¹)]} = (R:64)
8) Calcule as expressões:
a) ( 8 : 2) . 4 + {[(3² - 2³) . 2⁴ - 5⁰] . 4¹}= (R:76)
b) ( 3² - 2³) . 3³ - 2³ + 2² . 4² = ( R:83)
c) ( 2⁵ - 3³) . (2² - 2 ) = (R: 10)
d) [2 . (10 - 4² : 2) + 6²] : ( 2³ - 2²) = ( R:10)
e) (18 – 4 . 2) . 3 + 2⁴ . 3 - 3² . ( 5 – 2) = (R: 51)
f) 4² . [2⁴ : ( 10 – 2 + 8 ) ] + 2⁰ = (R: 17)
g) [( 4² + 2 . 3²) + ( 16 : 8)² - 35]² + 1¹⁰ - 10⁰ = (R : 9)
h) 13 + ( 10 – 8 + (7 – 4)) = (R: 18)
i) (10 . 4 + 18 – ( 2 . 3 +6)) = (R:46)
j) 7 . ( 74 – ( 4 + 7 . 10)) = (R: 0)
k) ( 19 : ( 5 + 3 . 8 – 10)) = (R : 1)
l) (( 2³ + 2⁴) . 3 -4) + 3² = (R: 77)
m) 3 + 2 . ((3²- 2⁰) + ( 5¹ - 2²)) + 1 = (R: 22)
9) Calcule as expressões:
a) 7 – ( 1 + 3)
b) 9 – ( 5 – 1 + 2)
c) 10 – ( 2 + 5 ) + 4
d) ( 13 – 7 ) + 8 – 1
e) 15 – ( 3 + 2) – 6
f) ( 10 – 4 ) – ( 9 -8) + 3
g) 50 – [ 37 – ( 15 – 8 ) ]
h) 28 + [50 – (24 – 2) -10 ]
i) 20 + [ 13 + (10 – 6) + 4]
j) 52 – { 12 + [ 15 – ( 8 – 4)]}
l) 25 + { 12 + [ 2 – ( 8 – 6 ) + 2 ]} = )
m) { [ ( 18 – 3 ) + ( 7 + 5) – 2 ] + 5 } – 12 = (R:18)n) 65 – { 30 – [ 20 – ( 10 – 1 + 6) + 1 ]} = (R: 41)
o)45 + { 15 – [ ( 10 – 8 ) + ( 7 – 4) – 3 ] – 4 } = (R:54)
p) 40 + { 50 – [35 – ( 25 +5) – 1 ]} + 7 = (R:93)
q)38 – { 20 – [ 22 – ( 5 + 3) + ( 7 – 4 +1)]} = ( R:36)
r) 26 + { 12 – [ ( 30 – 18) + ( 4 – 1) – 6 ] – 1 } = (R::28)
s) 25-[10 + (7 - 4)] = (R:12)
t) 32+ [10-(9-4)+8] = (R:45)
u)45-[12-4+(2+1)] = (R:31)
v)70-{20-[10-(5-1)]} = (R:56)
x) 28 + {13 - [6 -(4 + 1) + 2] - 1 } = (R:37)
z) 53-{20-[30-(15-1+6) + 2 ]} = (R:45)
10) Calcule as expressões:
a) [-7+14 : (5 - √ 49 ) ] : 7
b) [ -13 + 13 . ( -1 -3 . 2²)] : 14
c) -5 – [ (-5}² - (-2 -√9 ). 5 ] : 10
d) (-2)² - [ -2³ - √16 . ( 2³ - 10) ] : 171
e) 2 .[10-(3²- 4 . 5) - √9] : 18
f) 10 – [ 3º - (-2)³ - ( 4 – 8 : 2)] - √4
g) [(13 – 3 .4)³ - ( 18 – 4 . 5)³] : 3
h) 100 – {[25 + ( -2 – 1 )³] : 2 + √49} : 3
i) 100 – {[30 – ( 5 + 1)²] : 6 + √81 } : 8
j) 72. [ 4³ - ( √121 + 2 .26)]
l) 42 . [ 4. ( 32 – 4 . √49 ) -1 ] : 63
m) -5 + 2 .3² + 2 . √4
n) -6 + 2 . (-2)³ + 5 . 7º
o) 10 + 2 . 2² - 5 . √49
p) √100 + 3 .(-3)³- 2
q) 11 – 100 : (-10)
r) -13 + (-800) : 80
s) 5 – 2 . [ (-3) . (-2 – 6) : 4 + 15]
t) (3 -2 . 9 ) : 5
u) (3 – 2 .9) : (-5) : (-3)
v) ( 7 – 2 .14) : (-21) – ( 5 – 2 ) : 3
x) [(7 – 2 . 14) : (-21) – (5 – 2)] : 2
z) [4 – 2 . (3 – 7)] : (-2) -5
11) Calcule as expressões:
a) 1 – [7 – (4 – 3 . 2 ) . (-1 – 1)] . 5
b) 125 : (-5) : (-5)
c) (-64) : (-4) : (-4)
d) 5 + ( -3)² + 1 = (R:15)
e) 10 + (-2)³ -4 = (R:-2)
f) 12 – 1 + (-4)² = (R:27)
g) (-1)⁵ + 3 – 9 = (R:-7)
h) 18 – (+7) + 3² = (R:20)
i) 6 + (-1)⁵ - 2 = (R:3)
j) (-2)³ - 7 – (-1) = (R:-14)
l) (-5)³ - 1 + (-1)⁹ = (R:-127)
m) 5⁰ - ( -10) + 2³ = (R:19)
n) (-2)³ + (-3)² - 25 = (R:-24)
12) Calcule o valor das expressões:
a) 3 - 4² + 1 = (R:-12)b) 2³ - 2² - 2 = (R:2)
c) (-1)⁴ + 5 - 3² = (R:-3)
d) 5⁰ - 5¹ - 5⁰ = (R:-5)
e) (-3)². (+5) + 2 = (R:47)
f) (-1)⁷ - (-1)⁸ = (R:-2)
g) 5 + (-3)² + 7⁰ = (R:15)
h) √49 + 2³ - 1 = (R:14)
13) Calcule o valor das expressões:
a) (-3)² + 5 = (R:14)
b) (-8)² - (-9)² = (R:-17)
c) -72⁰ + (-1)⁸ = (R:0)
d) (-12)⁰ + (+12)⁰ = (R:2)
e) 10³ - (-10)² - 10⁰ = (R:899)
f) (-7)² + (-6)² - (-1)² = (R:84)
g) (-1)⁶ + (+1)⁵ + (-1)⁴ + (+1)³ = (R:4)
h) 2⁶ - 2⁵ - 2⁴ - 2³ - 2² - 2 = (R:2)
14) Calcule o valor das expressões:
a) (-3) . (+7) + (-8) . (-3) = (R:3)
b) (-3)³ + (+2)² - 7 = (R:-30)
c) 8 + (-3 -1)² = (R:24)
d) (-2 + 6)³ : (+3 – 5)² = (R:16)
e) –(-5)² + (-7 + 4) = (R:-28)
f) (-2)⁶ + (+5) . (-2) = (R:54)
15) Calcule o valor das expressões:
a) (-3)³ . (-2)² + (3) + 5⁰ = (R:-110)
b) (-1)³ + 3 + (+2) . (+5) = (R:12)
c) (-2) . (-7) + (-3)² = (R:23)
d) 2 . (-5)² - 3 . (-1)³ + 4 = (R:57)
e) –[ -1 + (-3) . (-2)]² = (R:-25)
f) –(5 – 7)³ - [ 5 - 2² - (4 – 6)] = (R:5)
g) (-3 + 2 – 1)³ - ( -3 + 5 – 1)⁸ + 3 = (R:-6)
h) 8 – [ -7 + )-1) . (-6) + 4]²= (R:-1)
i) 14 – [(-1)³ . (-2)² + (-35) : (+5)] = (R:25)
j) 5³ - [ 10 + (7 -8)² ]² - 4 + 2³ = (R:8)
k) (-1)⁸ + 6⁰ - [15 + (-40) : (-2)³ ] = (R:-18)
l) -3 –{ -2 – [(-35) : (+5) + 2² ]} = (R:-4)
16) Calcule o valor das expressões:
a) (- 3 + 5 + 2) : (-2) = (R:-2)
b) (+3 – 1)² - 15 = (R:-11)
c) (-2)³ - (-1 + 2)⁵ = (R:-9)
d) 40 : (-1)⁹ + (-2)³ - 12 = (R:-60)
e) 10 – [5 – (-2) + (-1)] = (R:4)
f) 2 – { 3 + [ 4 – (1 – 2) + 3 ] – 4} = (R:-5)
g) 15 – [ (-5)² - (10 - 2³ ) ] = (R:-8)
h) 13 – [(-2) – (-7) + (+3)² ] = (R:-1)
i) 7² - [ 6 – (-1)⁵ - 2²] = (R:46)
j) 2³ - [(-16) : (+2) – (-1)⁵] = (R:15)
k) 50 : { -5 + [ -1 –(-2)⁵ : (-2)³ ]} = (R:-5)
17) Calcule o valor das expressões:
a) 10 + (-3)² = (R:19)
b) (-4)² - 3 = (R:13)
c) 1 + (-2)³ = (R:-7)
d) -2 + (-5)² = (R:23)
e) (-2)² + (-3)³ = (R:-23)
f) 15 + (-1)⁵ - 2 = (R:12)
g) (-9)² -2 – (-3) = (R:82)
h) 5 + (-2)³ + 6 = (R:3)
18) Calcule o valor das expressões:
a) 5 – { +3 – [(+2)² -(-5)² + 6 – 4 ]} = (R:-17)
b) 15 – { -3 + [(5 – 6)² . (9 -8 ) ² + 1]} = (R:16)
c) 18 – { 6 – [ -3 – (5 – 4) – (7- 9)³ ] – 1 } = (R:17)
d) -2 + { -5 –[ -2 – (-2)³ - 3- (3 -2 )⁹ ] + 5 } = (R:-4)
e) 4 – {(-2)² . (-3) – [ -11 + (-3) . (-4)] – (-1)} = (R:16)
19) Efetue as subtrações:
a) (+5/7) – (+2/3) = (R: 1/21)b) (+2/3) – (+1/2) = (R: 1/6)c) (+2/3) – (+4/5) = (R: -2/15)
d) (-7/8) – (-3/4) = (R: -1/8)
e) (-2/5) – (-1/4) = (R: -3/20)
f) (-1/2) – (+5/8) = (R: -9/8)
g) (+2/3) – ( (+1/5) = (R: 7/15)
h) (-2/5) – ( +1/2) = (R: -9/10)
20) Efetue as subtrações:
a) (+1/2) – (+5) = (R: -9/2)
b) (+5/7) – (+1) = (R: -2/7)
c) 0 – ( -3/7) = (R:3/7)
d) (-4) – (-1/2) = (R: -7/2)
e) (+0,3) – (-1/5) = (R: ½)
f) (+0,7) – (-1/3) = (R:31/30)
21) Calcule
a) -1 – ¾ = (R: -7/4)
b) (-3/5) + (1/2) = (R: -1/10)
c) 2 – ½ -1/4 = (R: 5/4)
d) -3 -4/5 + ½ = (R: -33/10)
e) 7/3 + 2 -1/4 = (R: 49/12)
f) -3/2 + 1/6 + 2 -2/3 = (R: 0)
g) 1 – ½ + ¼ - 1/8 = (R:5/8)
h) 0,2 + ¾ + ½ - ¼ = (R:6/5)
i) ½ + (-0,3) + 1/6 = (R:11/30)
j) 1/5 + 1/25 + (-0,6) = (R: 1/10)
22) Calcule o valor de cada expressão:
a) 3/5 – 1 – 2/5 = (R: -4/5)
b) 3/5 – 0,2 + 1/10 = (R: ½)
c) -3 – 2 – 4/3 = (R: -19/3)
d) 4 – 1/10 + 2/5 = (R: 43/10)
e) 2/3 – ½ -5 = (R: 29/6)
f) -5/12 – 1/12 + 2/3 = (R: 1/6)
23) Calcule o valor de cada expressões:
a) -1/3 + 2/9 – 4/3 = (R: -13/9)
b) -4 + ½ - 1/6 = (R:-11/3)
c) 0,3 + ½ - ¾ = (R: 1/20)
d) 1 + ¼ - 3/2 + 5/8 = (R: 3/8)
e) 0,1 + 3/2 – ¼ + 2 = (R: 67/20)f) ¾ + 0,2 – 5/2 – 0,5 = ( R: - 41/20)
24) Calcule o valor de cada expressão
a) 1/2 – (-3/5) + 7/10 = (R: 9/5)
b) -(-1) – (- 4/3) + 5/6 = (R: 19/6)
c) 2 – ( - 2/3 – ¼) + 0,1 = (R: 181/60)
d) ( -1 + ½) – ( -1/6 + 2/3) = (R: -1)
e) 2 – [ 3/5 – ( -1/2 + ¼ ) ] = (R: 23/20)
f) 3 – [ -1/2 – (0,1 + ¼ )] = (R: 77/20)
g) (1/3 + ½) – (5/6.- ¾) = (R: ¾)
h) (5/2 – 1/3 – ¾ ) – (1/2 + 1) = (R: -1/12)
i) (1/4 + ½ + 2 ) + (-1/6 + 2/3) = (R: 13/4)
j) (-0,3 + 0,5 ) – ( -2 - 4/5) = (R: 3)
k) (1/6 + 2/3) – (4/10 – 3/5) + 1/3 = (R: 41/30)l) 0,2 + (2/3 – ¼) – ( -7/12 + 4/3) = (R: -2/15)
m) (1 – ¼) + (2 + ½) – (1 - 1/3) – ( 2 – ¼ ) = (R: 5/6)
Exercícios em forma de teste:
1) O resultado de (-1001)² é:
a) 11 011
b) -11 011
c) 1 002 001 X
d) -1 002 001
2) O valor da expressão 2⁰ - 2¹ - 2² é:
a) -4
b) -5 xc) 8
d) 0
3) O valor da expressão (-10)² - 10² é:
a) 0 x
b) 40
c) -20
d) -40
4) O valor da expressão √16 - √4 é
a) 2 xb) 4
c) 6
d) 12
5) O valor da expressão 10 + √9 – 1 é:
a) 14
b) 18
c) 12 x
d) 20
6) O valor da expressão (-4)⁴ - (-4) é :
a) 20
b) -20
c) 252
d) 260 x
7) O valor da expressão (-2)⁴ + (-9)⁰ - (-3)² é :
a) 8 x
b) 12
c) 16
d) -26
8) O valor da expressão (-7)² + (+3) . (-4) – (-5) é :
a) 7
b) 37
c) 42 x
d) 47
9) A expressão (-7)¹⁰ : (-7)⁵ é igual a:
a) (-7)⁵ x
b) (-7)²
c) (-7)¹⁵
d) (-1)²
10) O valor da expressão –[-2 + (-1) . (-3)]² é :
a) -1 xb) -4
c) 1
d) 4
11) O valor da expressão numérica -4² + (3 -5) . (-2)³ + 3² - (-2)⁴ é
a) 7
b) 8
c) 15
d) -7 x
http://jmpmat11.blogspot.com/
Reprodução das Aves
As aves são animais dióicos (existem machos e fêmeas) e ovíparos, frequentemente mostram um dimorfismo sexual muito marcante, sendo os machos mais vistosos do que as fêmeas, com penas maiores e mais coloridas, são comuns também grandes papos e cristas de cores bem vibrantes, e isto é que faz com que o macho atraia a fêmea para fazerem um ninho e formarem uma ninhada.
ninhada avespavaoOutras aves realizam complexos e curiosos rituais de danças a dois (macho e fêmea) e diversas posturas corporais quando pretendem acasalar. Na sua época de reprodução, as aves podem ficar seus territórios onde constituem seus ninhos, que geralmente é um local alto e seguro, e estes ninhos servem para incubação dos ovos, onde a fêmea os depositam.
Apesar da maioria das espécies de aves machos não possuírem órgão copulador (pênis), a fecundação é interna. A transferência de espermatozóides para fêmea ocorre pela justaposição das aberturas das cloacas de ambos durante a cópula. Após a cópula as fêmeas eliminam os ovos pela cloaca no ninho, e estes ovos (ricos em vitelo) são protegidos por uma casca calcária.
O ovo já pronto, então, zigoto, protegido por invólucros, são encubados nos ninhos, pelos pais, e então ocorre seu desenvolvimento. Durante a incubação o macho ou a fêmea ou ambos, em rodízio, assentam-se no ovo para manter em uma temperatura adequada, e com certa frequência com o bico rolam o ovo para que de certo modo o calor de seus corpos distribua uniformemente por toda a superfície desses ovos. Dentro dos ovos mais ou menos em média de duas semanas o embrião se desenvolve até torna-se uma pequena ave.
Após essa formação ocorre a eclosão dos ovos e os filhotes demonstram um comportamento que chamamos de nidífugo, ou seja, já estão bem formados o suficiente para caminhar ou nadar, acompanhando os pais em busca de alimento. Mas também podem ocorrer ao contrário as aves nidícolas são, aqueles filhotes que nasceram muito imaturos e permanecem no ninho até adquirirem penas e força muscular para terem a capacidade de voar, se tornando assim independentes, mas enquanto não adquirem penas e força muscular seus pais, vão em busca de alimento e armazenam no bico, até que possam chegar no ninho e alimentar os seus filhotes ainda imaturos. Este processo é o das aves voadoras.
Os ovos não fecundados são chamados de ovos não-galados.
Fontes:
Biologia Vol. 1 – José Mariano Amabis & Gilberto Rodrigues Martho
Biologia Vol.2 – César e Sezar
Biologia atual Vol. 2 – Wilson Roberto Paulino
http://pinfotos.abril.com.br/busca/tags/aves/699c15b6-16f9-4f79-86c1-4b30ae964c73/ave_alimentando_os_filhotesjpg
http://jornalanimais.blogspot.com/2009/08/colibri-formula-um-dos-passaros.html
http://www.eb1-brunheiras-n1.rcts.pt/aves.htm
ninhada avespavaoOutras aves realizam complexos e curiosos rituais de danças a dois (macho e fêmea) e diversas posturas corporais quando pretendem acasalar. Na sua época de reprodução, as aves podem ficar seus territórios onde constituem seus ninhos, que geralmente é um local alto e seguro, e estes ninhos servem para incubação dos ovos, onde a fêmea os depositam.
Apesar da maioria das espécies de aves machos não possuírem órgão copulador (pênis), a fecundação é interna. A transferência de espermatozóides para fêmea ocorre pela justaposição das aberturas das cloacas de ambos durante a cópula. Após a cópula as fêmeas eliminam os ovos pela cloaca no ninho, e estes ovos (ricos em vitelo) são protegidos por uma casca calcária.
O ovo já pronto, então, zigoto, protegido por invólucros, são encubados nos ninhos, pelos pais, e então ocorre seu desenvolvimento. Durante a incubação o macho ou a fêmea ou ambos, em rodízio, assentam-se no ovo para manter em uma temperatura adequada, e com certa frequência com o bico rolam o ovo para que de certo modo o calor de seus corpos distribua uniformemente por toda a superfície desses ovos. Dentro dos ovos mais ou menos em média de duas semanas o embrião se desenvolve até torna-se uma pequena ave.
Após essa formação ocorre a eclosão dos ovos e os filhotes demonstram um comportamento que chamamos de nidífugo, ou seja, já estão bem formados o suficiente para caminhar ou nadar, acompanhando os pais em busca de alimento. Mas também podem ocorrer ao contrário as aves nidícolas são, aqueles filhotes que nasceram muito imaturos e permanecem no ninho até adquirirem penas e força muscular para terem a capacidade de voar, se tornando assim independentes, mas enquanto não adquirem penas e força muscular seus pais, vão em busca de alimento e armazenam no bico, até que possam chegar no ninho e alimentar os seus filhotes ainda imaturos. Este processo é o das aves voadoras.
Os ovos não fecundados são chamados de ovos não-galados.
Fontes:
Biologia Vol. 1 – José Mariano Amabis & Gilberto Rodrigues Martho
Biologia Vol.2 – César e Sezar
Biologia atual Vol. 2 – Wilson Roberto Paulino
http://pinfotos.abril.com.br/busca/tags/aves/699c15b6-16f9-4f79-86c1-4b30ae964c73/ave_alimentando_os_filhotesjpg
http://jornalanimais.blogspot.com/2009/08/colibri-formula-um-dos-passaros.html
http://www.eb1-brunheiras-n1.rcts.pt/aves.htm
Assinar:
Postagens (Atom)