Fatorial

Professor de Matemática no Colégio Estadual Dinah Gonçalves

E Biologia na rede privada de Salvador-Bahia

Professor Antonio Carlos carneiro Barroso

email accbarroso@hotmail.com

Blog HTTP://ensinodematemtica.blogspot.com.br e HTTP://accbarroso60.wordpress.com www.accbarrosogestar.wordpress.com

Extraído de http://www.alunosonline.com.br

Fatorial

Marcos Noé

Fatorial de um número

O fatorial de um número consiste em um importante mecanismo nos estudos envolvendo Análise Combinatória, pois a multiplicação de números naturais consecutivos é muito utilizada nos processos de contagem. Fatorial de um número consiste em multiplicar o número por todos os seus antecessores até o número 1.

Observe a definição a seguir:
Representamos o fatorial de um número por n! e o desenvolvimento por n! = n * (n – 1) * (n – 2) * (n – 3) * ... * 4 * 3 * 2 * 1 para n ≥ 2. Caso n = 1, temos 1! = 1 e n = 0, temos 0! = 1.

Exemplo 1

3! = 3 * 2 * 1 = 6
4! = 4 * 3 * 2 * 1 = 24
5! = 5 * 4 * 3 * 2 * 1 = 120
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
8! = 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 40 320
9! = 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 362 880
10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3 628 800


Alguns cálculos envolvendo fatorial exigem algumas técnicas de simplificação e fatoração. Observe as demonstrações a seguir:

Exemplo 2

Vamos calcular o valor de 12! / 8! . Nesse caso, se desenvolvermos os fatoriais dos números e depois efetuarmos a divisão, o método de resolução estará correto. Mas essa forma de resolução pode se tornar complexa para números elevados, por isso devemos desenvolver o fatorial do maior número até chegarmos ao fatorial do menor número, simplificando os fatoriais semelhantes. Observe:


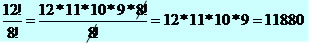
Exemplo 3

Outra forma de resolução de fatoriais é quando ocorre a soma de fatoriais. Nesse caso podemos utilizar a fatoração por evidência. Observe:

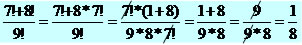
Exemplo 4

Outras situações exigem técnicas de desenvolvimento dos fatoriais para que simplificações sejam efetuadas. Veja:


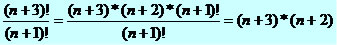
n² + 2n + 3n + 6
n² + 5n +6


Exemplo 5

O fatorial de um número também está associado a equações. Observe os cálculos:

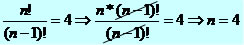
Solução = {4}


Exemplo 6

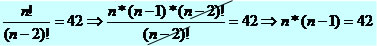
n² – n = 42
n² – n – 42 = 0

Desenvolvendo a equação do 2º grau temos:

n’ = 7 e n” = – 6

n = – 6 não convém, pois fatorial só é aplicado a números naturais. Portanto, S = {7}.