Sistemas de Equações

Professor de Matemática no Colégio Estadual Dinah Gonçalves

E Biologia na rede privada de Salvador-Bahia

Professor Antonio Carlos carneiro Barroso

email accbarroso@hotmail.com

Blog HTTP://ensinodematemtica.blogspot.com e HTTP://accbarroso60.wordpress.com

http://accbarrosogestar.blogspot.com.br

Sistemas de Equações

Por Marcos Noé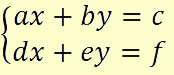

Sistema linear

Os sistemas de equações consistem em ferramentas importantes na Matemática, eles são utilizados para determinar os valores de x e y nas equações com duas variáveis. A resolução dos sistemas consiste em estabelecer uma relação entre as equações e aplicar técnicas de resolução. Os métodos usados na resolução de um sistema são: substituição e adição. Exemplos de sistemas de equações:

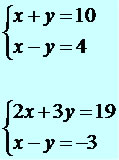
Método da Substituição

O método da substituição consiste em trabalhar qualquer equação do sistema de forma a isolar uma das incógnitas, substituindo o valor isolado na outra equação. Observe passo a passo a resolução do sistema a seguir:

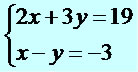
Nesse caso, vamos escolher a 2º equação e isolar a incógnita x.

x – y = –3
x = –3 + y

Agora, substituímos o valor de x por –3 + y na 1º equação.

2x + 3y = 19
2*(–3 + y) + 3y = 19
–6 + 2y + 3y = 19
2y + 3y = 19 + 6
5y = 25
y = 5

Para finalizar, calculamos o valor de x utilizando a seguinte equação:

x = –3 + y
x = –3 + 5
x = 2

Portanto, a solução do sistema é x = 2 e y = 5, isto é, o par ordenado (2,5)



Método da Adição

O método da adição deve ser utilizado nos sistemas em que existe a oportunidade de zerar uma das incógnitas. Observe a resolução do sistema a seguir:

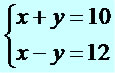
1º passo: somamos as equações, eliminando uma das incógnitas e determinando o valor da outra incógnita.

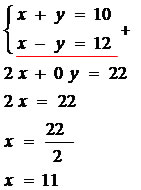
Calculado o valor de x, basta escolher uma das equações e substituir o valor de x por 11.

x + y = 10
y = 10 – x
y = 10 – 11
y = –1

A solução do sistema é o par ordenado (11, –1).

Desafios

Desafios

1) Observe as multiplicações a seguir:
12 345 679 x 18 = 222 222 222
12 345 679 x 27 = 333 333 333
12 345 679 x 54 = 666 666 666
Para obter 999 999 999 devemos multiplicar 12 345 679 por quantos?

2) Outro dia ganhei 250 reais, incluindo o pagamento de horas extras. O salário (sem horas extras) excede em 200 reais o que recebi pelas horas extras. Qual é o meu salário sem horas extras?

3) O número 10 pode ser escrito de duas formas como soma de dois números primos:
10 = 5 + 5 e 10 = 7 + 3. De quantas maneiras podemos expressar o número 25 como uma soma de dois números primos?

4) Um certo número N de dois algarismos é o quadrado de um número natural. Invertendo-se a ordem dos algarismos desse número, obtém-se um número ímpar. A diferença entre os dois números é o cubo de um número natural. Determine a soma dos algarismos de N.

5) A prefeitura de uma certa cidade fez uma campanha que permite trocar 4 garrafas de 1 litro vazias por uma garrafa de 1 litro cheia de leite. Até quantos litros de leite pode obter uma pessoa que possua 43 dessas garrafas vazias?

6) Quantos são os números inteiros de 2 algarismos que são iguais ao dobro do produto de seus algarismos?
extraido de www.mundoeducacao.com.br

Equações de 1º grau fracionárias

Ativ minha 7ª serie 2011

View more documents from Antonio Carlos.

Potência e raiz quadrada de fração

Regra do octeto Átomo nobre tem oito eletrons na camada de valência

Os gases nobres, hélio, neônio, argônio, criptônio, xenônio e radônio, se destacam entre todos os elementos químicos por apresentarem uma estabilidade única, que os torna inertes à reação com quase todos os outros elementos.

Normalmente tais gases se apresentam como átomos isolados e não como moléculas, estabelecendo ligações atômicas apenas em condições muito especiais.

É claro que características tão particulares chamaram a atenção dos químicos, que se propuseram a entender o que estes átomos possuíam de diferente dos outros para apresentar tal comportamento.

A resposta veio da análise do modo como os elétrons se distribuíam ao longo das camadas destes átomos, conforme descrito na tabela que segue:

Distribuição Eletrônica dos Gases Nobres
Gás Nobre

Noatômico

Distribuição dos eletrons por camadas
1a

2a

3a

4a

5a

6a
He

2

2

Ne

10

2

8

Ar

18

2

8

8

Kr

36

2

8

18

8

Xe

54

2

8

18

18

8

Ra

86

2

8

18

32

18

8

Com exceção do hélio, todos os gases nobres possuem oito elétrons em sua camada de valência, aquela última na qual ocorrem as ligações moleculares ou iônicas.

Assim, um átomo que completa a última camada de sua eletrosfera com oito elétrons adquire as características de um gás nobre, ou seja, torna-se estável.

Um exemplo próximo de todos é a molécula de água.

Vejamos a distribuição eletrônica do oxigênio:

Número atômico

1acamada

2acamada
8

2

6

Para obedecer à regra do octeto, o oxigênio precisa para se estabilizar de mais dois átomos na última camada.

Assim temos o porquê de nossa conhecida fórmula H2O, já que na molécula de água cada um dos átomos de hidrogênio compartilha numa ligação covalente um elétron com o átomo de oxigênio, que assim passa a somar em sua última camada os oitos que precisava para sua estabilidade, conforme figura seguinte:


Pela mesma razão, a molécula de oxigênio O2 é formada pelo compartilhamento de dois pares eletrônicos por cada átomo da ligação, conforme se vê abaixo:


Notem na figura que pela ligação molecular, os dois átomos de oxigênio compartilham quatro elétrons (dupla ligação), constituindo assim, oito elétrons em sua última camada. Já a molécula do nitrogênio, N2, cujos átomos têm número atômico 7 e distribuição eletrônica 2-5, precisa, para cumprir a regra do octeto, de mais três elétrons na última camada.

Isto é obtido através de uma tripla ligação, na qual cada átomo compartilha três elétrons com o outro membro da ligação, conforme figura abaixo:

Moléculas de Nitrogênio, com tripla ligação e molécula de Hidrogênio. O H2 não obedece a Regra do Octeto

Na figura, além da molécula de nitrogênio, podemos observar a molécula de hidrogênio, que, obviamente, não obedece à regra do octeto.

Isto se dá pelo fato de estarmos falando de uma regra e não de uma lei da química.

Assim, não só o hidrogênio, que encontra a estabilidade numa distribuição eletrônica semelhante à do helio, mas também outros elementos químicos não necessariamente seguem o padrão de formar ligações que complementem suas camadas finais com oito elétrons.

Isto pode ser concluído de uma simples observação da tabela periódica.

Os elementos situados nos grupos 3 a 12 da tabela, também chamados de elementos de transição, têm distribuições eletrônicas que dificultam o cumprimento da regra do octeto, pois teriam que trocar ou compartilhar um número relativamente grande de elétrons para adequarem-se àquela Regra.

A regra do octeto é cumprida de modo geral nos grupos 1 e 2 e do 13 ao 18, onde se situam os elementos químicos que podem completar os elétrons da última camada com ligações atômicas envolvendo poucos elétrons.
Carlos Roberto de Lana é engenheiro químico e professor.

Solubilidade de compostos orgânicos

A solubilidade de uma substância é uma propriedade física muito importante, na qual se baseiam certos métodos de separação de misturas, de extração de produtos naturais e de recristalização de substâncias.

Também é uma propriedade muito empregada nas industrias de tintas, perfumes, sabões e detergentes, açúcares e plásticos. A solubilidade depende da natureza do soluto, do solvente e da temperatura.

Para prever o comportamento de certos solutos em relação a certos solventes (à temperatura constante) é necessário se analisar as suas estruturas moleculares, ou melhor, o tipo de interação que há entre soluto e solvente.

De acordo com as Regras de Solubilidade, uma substância polar tende a dissolver em um solvente polar, e uma substância apolar também num solvente apolar. Ou seja, semelhante dissolve semelhante. Por esse motivo as substâncias orgânicas em geral, só se dissolvem em líquidos também orgânicos, como, por exemplo, álcool, éter, benzeno, gasolina, etc. Esses líquidos recebem o nome de solventes orgânicos.

Outra consideração que devemos fazer é a seguinte: quando a temperatura de uma solução diminui ou quando o solvente evapora, o soluto tende a cristalizar, purificando-se, mas, devemos notar que:

* A cristalização de uma substância iônica é mais fácil, pois, os íons se atraem eletricamente;

* Pelo contrário a cristalização de uma substância molecular é mais difícil, pois a atração entre as moléculas é muito menor. A cristalização das substâncias orgânicas é em geral difícil e demorada. Existem certos compostos orgânicos como a parafina, que não se cristalizam. Os compostos orgânicos cristalinos surgem entre os compostos orgânicos bastante polares (caso dos açucares) ou entre os compostos orgânicos iônicos (como exemplo, os sais orgânicos).

Após muitos anos de estudos, chegou-se a conclusão que é conveniente distribuir os compostos orgânicos em sete grupos de solubilidade, com base em:

1. Sua solubilidade em relação à água, éter, solução aquosa de hidróxido de sódio a 5%, ácido clorídrico a 5%, ácido concentrado frio.

2. Nos elementos que eles contém além do carbono e hidrogênio.

Os grupos resultantes desta classificação são:

* Grupo I: Compostos solúveis tanto em éter quanto em água.

* Grupo II: Compostos solúveis em água, mas insolúveis em éter.

* Grupo III: Compostos insolúveis em água, mas solúveis em hidróxido de sódio diluído. Este grupo ainda foi dividido em:
Grupo III-A: compostos solúveis em hidróxido de sódio diluído e solúveis em bicarbonato de sódio diluído.
Grupo III-B: compostos solúveis em hidróxido de sódio diluído e insolúveis em bicarbonato de sódio, diluído.

* Grupo IV: Compostos insolúveis em água, mas solúveis em ácido clorídrico diluído.

* Grupo V: Hidrocarbonetos e compostos contendo C, H e O que não sejam aqueles dos Grupos I a IV e sejam solúveis em ácido sulfúrico concentrado ("compostos indiferentes").

* Grupo VI: Todos os compostos que não contenham N ou S e que sejam insolúveis em ácido sulfúrico concentrado.

* Grupo VII: Compostos que contenham N ou S que não sejam aqueles dos Grupos I a IV. Muitos dos compostos deste grupo são solúveis em ácido sulfúrico concentrado.
www.coladaweb.com/

Números inteiros

A subtração é uma operação básica da Matemática, sendo representada pelo sinal de –. O desenvolvimento da subtração entre números Naturais é de certa forma bem simples. Observe os exemplos:

10 – 2 = 8
12 – 6 = 6
22 – 10 = 12
52 – 12 = 40
101 – 10 = 91
200 – 189 = 11

As operações de subtração envolvendo os números Inteiros requerem algumas situações teóricas que relacionam os possíveis sinais operatórios. Para realizar a subtração entre os números inteiros precisamos ter conhecimento sobre o módulo de um número. Módulo de um número inteiro é calculado obtendo o seu valor real. Observe:

Módulo de +1: representado por |+1| = 1
| – 3| = 3
| – 7| = 7

Regras operatórias:
Sinais iguais: soma e conserva o sinal.
Sinais diferentes: subtrai e conserva o sinal do maior módulo.

Operações sem parênteses

+ 10 – 7 = + 3 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)

– 3 – 3 = – 6 (Sinais iguais: soma e conserva o sinal)

+ 20 – 30 = – 10 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)

– 12 + 3 = – 9 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)

– 9 + 9 = 0 (operação entre números opostos, resultado sempre será 0)

– 25 + 24 = – 1 (Sinais diferentes: subtrai e conserva o sinal do maior módulo)


Operações com parênteses

Nesse caso, as operações de subtração podem ser resolvidas eliminando os parênteses, isso será feito aplicando algumas regras que envolvem jogo de sinal, observe:

+ (+) = +
+ (–) = –
– (+) = –
– (–) = +

Eliminado os parênteses, passa a valer as regras operatórias:

(+10) – (–23) = +10 + 23 = + 33

(+20) – (+12) = +20 – 12 = + 8

(–32) + (–5) = – 32 – 5 = – 37

(–27) – (–30) = –27 + 30 = + 3
http://www.mundoeducacao.com.br

Conjunto

1- Naturais (IN)

N = {0,1,2,3,4,5...}

Convém destacar um subconjunto: N* = N - {0} = {1,2,3,4,5...}

É importante lembrar que sempre é possível efetuar a adição e a multiplicação, isto é, a soma e o produto de dois números naturais sempre terá como resultado um número natural, já a subtração entre dois números naturais nem sempre é um número natural, como por exemplo 2 ? 5, não pertence aos N, temos então o surgimento do conjunto dos números inteiros.

2- Inteiros (Z)

Z = {...-3,-2,-1,0,1,2,3...}

No conjunto dos inteiros destacamos os seguintes subconjuntos:

Z* = Z - {0} = {...-3,-2,-1,1,2,3...}

Z+ = {0,1,2,3,4...} (inteiros não negativos)

Z - = {0,-1,-2,-3,-4...} (inteiros não positivos)

Z*+ = {1,2,3,4...} (inteiros positivos)

Z*- = {-1,-2,-3,-4...} (inteiros não negativos)

Neste conjunto sempre é possível efetuar a adição, a multiplicação e a subtração entre números inteiros, isto é, sempre estas operações resultam em um número inteiro. Já a divisão nem sempre resulta em um número inteiro, como por exemplo, 7 : 2 ,não pertence aos inteiros surgindo assim o conjunto dos racionais.

3-Racionais (Q)

Q = {x tal que x = a/b (a sobre b) onde aÎ (pertence) Z a b E Z* (Z menos o zero)}.

O conjunto dos números racionais Q é a união do conjunto dos números naturais (N), inteiros (Z) e as frações positivas e negativas, como por exemplo:

Q = -5 ; - 4/3 ; - 1; 0; 0,25 ; 1/2 ; 3/4 ; 1; 6/5 ; 2

Obs: Um número racional pode aparecer em forma de dízima periódica, isto é, um numeral decimal, com a parte decimal formada por infinitos algarismos que se repetem periodicamente, como por exemplo: 4,5555 (período 5) , 10,878787 (período 87) e 9,8545454... (período 54, parte não periódica 8)

Exemplo: transformar em frações irredutíveis os números:

a) 0,1111....

x=0,111...

10x=1,111...

daí,

10x-x=1

x=1/9

portanto, 0,111...=1/9

b) 2,1343434...

x=2,1343434...

10x=21,3434...

1000x=2134,3434....

daí,

1000x-10x=2113

x=2113/990

portanto, 2,1343434...=2113/990

4-Irracionais (I) ? É todo número decimal não-exato e não periódico, bem como toda raiz não-exata.

- raiz quadrada de dois = 1,414...;
- raiz quadrada de três = 1,73...;
- dízimas não periódicas;

5-Reais (IR)

Combustíveis

A produção e fornecimento de combustível

O combustível é caracterizado por ser qualquer substância que, ao reagir com o oxigênio, produz calor, gases ou chamas. A energia liberada durante esse processo é de fundamental importância para as atividades humanas e, principalmente, para a produção industrial, pois grande parte das máquinas funciona a partir de energia combustível.

Várias substâncias podem ser utilizadas na fabricação de combustível, sendo os de origem fóssil os mais populares (petroléo, carvão e gás natural). Porém, a necessidade de desenvolver alternativas que possam substituir, gradativamente, os combustíveis de origem fóssil, impulsionou as pesquisas para a obtenção de biocombustível.

A cana-de-açúcar, os resíduos agropecuários, o dendê, plantas oleaginosas e a biomassa florestal são as principais matérias-primas na produção do biocombustível, que é um dos menos agressivos ao meio ambiente, pois a emissão de gases poluentes é praticamente nula.

Nessa seção, estão disponibilizados textos sobre a classificação e caracterização dos combustíveis, principais substâncias utilizadas na sua produção, aspectos geopolíticos do petróleo, entre outros temas pertinentes.

Uma ótima leitura a todos!

Wagner de Cerqueira e Francisco

Arqueologia

Arqueologia

O estudo do comportamento humano é de fundamental importância para compreendermos aspectos da organização espacial. Através da Arqueologia, ciência responsável pelo estudo do passado por meio de vestígios materiais, é possível identificar e analisar objetos de civilizações da antiguidade, proporcionando informações sobre sua cultura e o seu modo de vida.

Os primeiros registros de estudos arqueológicos são oriundos do século XVI, durante o movimento Renascentista. Nesse momento teve início uma série de discussões acerca do método utilizado para analisar os estágios da organização social em diferentes períodos.

Com o passar das décadas, o desenvolvimento de novas técnicas exerceu grande importância para o estudo arqueológico, passando a ser utilizados instrumentos de precisão que auxiliam nas escavações e análises dos artefatos.

Nessa seção, o leitor poderá se inteirar sobre os aspectos elementares da Arqueologia, visto que estão disponibilizados textos sobre o conceito dessa ciência, seu histórico, o método utilizado para se encontrar um sítio arqueológico, características dos fósseis, além de uma “viagem ao passado”, através de uma série de seis artigos.

A análise crítica desse material fornece subsídios para entendermos o comportamento de civilizações antigas, como os indivíduos se relacionavam, as primeiras formas de escrita, a representação dos aspectos naturais, os artefatos, etc.

Boa leitura, ou melhor, boa “viagem” ao passado.

Wagner de Cerqueira e Francisco

Os continentes

Os seis continentes terrestres

A Terra apresenta 149.440.850 quilômetros quadrados de áreas emersas, correspondendo a aproximadamente 29,1% da superfície total do planeta. Essas grandes extensões de terras são dividas em seis continentes: África, América, Antártica, Ásia, Europa e Oceania.

Porém, é importante elucidar que, há cerca de 400 milhões de anos, as porções emersas do planeta estavam reunidas em um único continente, denominado Pangeia. Esse grande continente se fragmentou há aproximadamente 60 milhões de anos em razão do movimento das placas tectônicas, formando os atuais seis continentes.

Os limites entre os continentes são estabelecidos principalmente por mares e oceanos. No entanto, os continentes europeu e asiático formam uma massa de terra, denominada Eurásia. As fronteiras entre eles são estabelecidas por meio dos Montes Urais, Rio Ural, Mar Cáspio, Montanhas do Cáucaso e pelo Mar Negro.

O estudo dos seis continentes é de fundamental importância para entendermos vários aspectos relacionados ao estudo da Geografia. A abordagem desse conteúdo proporciona subsídios para uma análise do atual cenário econômico global, organização social, desigualdade socioeconômica, disparidades entre os continentes, concentração populacional, elementos culturais, aspectos naturais do planeta, entre outros temas pertinentes.

Nesse sentido, disponibilizamos uma seção com artigos que abordam diversos assuntos sobre os seis continentes terrestres, na qual o leitor poderá se inteirar sobre as principais características de cada um deles.

Boa leitura!

Wagner de Cerqueira e Francisco

Operações com decimais

Multiplicação de número natural por decimal.

A operação de multiplicação e operada com dois fatores e a multiplicação deles resulta em um produto.

6 x 3,25 → são os fatores

1 3
3,25 → fator
x 6 → fator
19,50 → produto

Na multiplicação acima:
Quando multiplicamos 5 centésimos por 6 obtivemos 30 centésimos. Deixamos 0 centésimos e transformamos os 30 centésimos em 3 décimos.
Quando multiplicamos 2 décimos por 6 e somamos com 3 obtivemos 15 décimos, deixamos 5 décimos e transformamos os 10 décimos em 1 inteiro.

Para colocarmos a vírgula na casa decimal correta no produto (resultado da multiplicação) devemos olhar o número decimal do fator e contar quantas casas decimais ele tem, no caso do 3,25 tem 2 casas decimais, então devemos contar da direita para a esquerda 2 casas decimais no produto e colocar a vírgula na casa decimal correspondente.


12 x 9,3 → são os fatores

Quando em uma multiplicação o 2º fator for um número natural com mais de um algarismo, devemos multiplicar com o da direita e depois fazer a multiplicação com o da esquerda. O resultados das multiplicações somamos.

9,3
x 1 2
1 1 8 6
+ 9 3
11 1,6


Para colocarmos a vírgula na casa decimal correta no produto (resultado da multiplicação) devemos olhar os números decimais dos fatores e contar quantas casas decimais ele tem, no caso do 9,3 tem 1, então andaremos da direita para a esquerda 1 casa decimal e colocaremos a virgula onde paramos.

Multiplicação de decimal por decimal

Para multiplicarmos decimal com decimal resolveremos da mesma forma se fosse multiplicação de número natural com decimal, o que difere é quando formos colocar a vírgula no produto devemos contar as casas decimais dos dois fatores.

9 , 3
x 1, 2
1 1 8 6
+ 9 3
11, 16

Como somando as casas decimais dos dois fatores, teremos 2 casas decimais, assim andaremos 2 casas decimais da direita para a esquerda para colocarmos a vírgula.

Preposição

preposição.

Preposição é uma palavra invariável que estabelece uma relação subordinada entre as palavras.

Exemplo:

O quarto de Marcio é grande; (a palavra quarto -substantivo- tem de estar ligada com Marcio, usando-se assim a preposição de).

Ela foi para casa; (a palavra para liga o verbo ir com o substantivo casa, usando a preposição para).

O que antecede a uma preposição pode ser um substantivo, um adjetivo, um pronome, ou um verbo.

Locução Prepositiva.

As locuções prepositivas geralmente são formadas pela junção de um advérbio e de uma preposição, estas ipedlink3servem como preposições (acima de, através de, depois de, devido a, para com, a fim de, abaixo de, e etc.).

A menina veio depois de você.

Devido a falta de luz não haverá aula.

Classificação

As preposições classificam-se em:

Essenciais: possuem o valor de preposição: a, ante, após, até, com, contra, de, desde, em, entre, para, per, perante, por, sem, sob, sobre, trás.
Acidentais: estas palavras constituem outras classes, porém, são usadas com preposição: conforme, segundo, consoante, como, afora, mediante, durante.

Combinação e Contração.

Algumas preposições como - a, em, de e per-, podem se juntar a outra palavra.

Veja:

Combinação (não possui alteração fônica).
(a + o) = ao.
(a + onde) = aonde.

Contração (possui alteração fônica).
(a + a) = à.
(de + o) = do.
(de + onde) = donde.
www.colegioweb.com.br