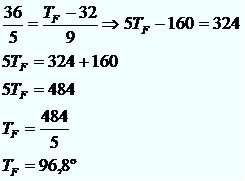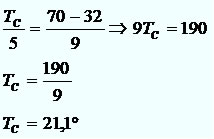Numero racional é todo o numero que pode ser escrito na forma a/b (com b diferente de zero)
Exemplos
a) 5 = 5/1
b) -2 = -2/1
c) 0,7 = 7/10
d) 2,83 = 283/100
e) 0,444... = 4/9
f) 0,7272... 72/99
Observe que:
- todo o número inteiro é um número racional
- toda decimal exata é um número racional
- toda decimal periódica é um número racional
NÚMEROS IRRACIONAIS
Os números que não podem ser escritos em forma de fração são chamados de números irracionais , os números irracionais têm infinitas casas decimais e não são periódicas.
Exemplos
a) 0,4137128.....
b) 7,1659314....
c) -0,4837616...
d) -2,8283541....
As raízes quadradas de números que não são quadrados perfeitos são também exemplos de números irracionais.
a) √2 = 1,4142....
b) √3 = 1,7320....
NUMEROS REAIS
A união dos conjuntos dos números racionais e irracionais chama-se conjunto dos números reais que será indicado com IR .
Exemplos
a) ¾ é um número racional. É também um número real
b) √7 é um número irracional .É também um número real
Obs: que todo o número natural é inteiro, todo o numero inteiro é também racional e todo o racional é também real
OPERAÇÕES EM IR – PROPRIEDADES
Todas as operações estudadas em Q e suas respectivas propriedades também são validas em IR. Para quaisquer numero reais a, b, c, temos:
ADIÇÃO
1) Fechamento
(a + b) € IR
2) Comutativa
a + b = b + a
3) Associativa
(a + b ) + c = a + ( b + c)
4) Elemento Neutro
a + 0 = 0 + a = a
5) Elemento oposto
a + (-a) = 0
MULTIIPLICAÇÃO
1) Fechamento
(a . b) € IR
2) Comutativa
a . b = b . a
3) Associativa
( a . b) . c = a . ( b . c)
4) Elemento Neutro
a . 1 = 1 . a = a
5) Elemento inverso
a . 1/a = 1 ( a ≠ 0 )
VALOR NUMÉRICO DE UMA EXPRESSÃO ALGÉBRICA
Observe os dois tipos de expressão matemáticas:
Expressão numéricas
a) 7 -1 + 4
b) 2. 5 – 3
c) 8² - 1 + 4
Expressões Algébricas
a) x + y – z
b) 2x – 4ª + 1
c) 3x² - 5x + 9
Expressões numéricas – possuem apenas números.
Expressões algébricas – possuem números e letras ou apenas letras
VALOR NÚMERICO DE UMA EXPRESSÃO ALGÉBRICA
Para obter o valor numérico de uma expressão algébrica, você deve proceder do seguinte modo:
1º Substituir as letras por números reais dados.
2º Efetuar as operações indicadas, devendo obedecer à seguinte ordem:
a) Potenciação
b) Divisão e multiplicação
c) Adição e subtração
IMPORTANTE!
Convém utilizar parênteses quando substituímos letras por números negativos
Exemplo 1
Calcular o valor numérica de 2x + 3a
para x = 5 e a = -4
2.x+ 3.a
2 . 5 + 3 . (-4)
10 + (-12)
-2
Exemplo 2
Calcular o valor numérico de x² - 7x +y
para x = 5 e y = -1
x² - 7x + y
5² - 7 . 5 + (-1)
25 – 35 -1
-10 – 1
-11
Exemplo 3
Calcular o valor numérico de :
2 a + m / a + m ( para a = -1 e m = 3)
2. (-1) + 3 / (-1) + 3
-2 + 3 / -1 +3
½
Exemplo 4
Calcular o valor numérico de 7 + a – b (para a= 2/3 e b= -1/2 )
7 + a – b
7 + 2/3 – (-1/2)
7 + 2/3 + 1 / 2
42/6 + 4/6 + 3/6
49/6
EXERCICIOS
1) Calcule o valor numérico das expressões:
a) x – y (para x =5 e y = -4)
(R:9)
b) 3x + a (para x =2 e a=6)
(R: 12)
c) 2x + m ( para x = -1 e m = -3)
(R: -5)
d) m – 2 a ( para m =3 e a = -5)
(R: 13)
e) x + y ( para x = ½ e y = -1/5)
(R: 3/10)
f) a –b ( para a =3 e b = -1/2)
(R: 7/2)
2) Calcule o valor numérico das expressões
a) a³ - 5 a (para a = -2)
(R: 2)
b) x² - 2y ( para x = -3 e y =5)
(R: -1)
c) 3a² - b² (para a = -2 e b = -7)
(R: -37)
d) 5a² + 3ab (para a = -3 e b = 4)
(R: 19)
e) a² + 4a (para a = 2/3)
(R: 28/9)
EXPRESSÕES ALGÉBRICAS
TERMO ALGÉBRICO OU MONÔMIO
Um produto de números reais, todos ou em parte sob representação literal, recebe o nome de monômio ou termo algébrico
Exemplos
a) 7x
b) 4/5 a²
c) -5x²y
d) –xyz
Em todo monômio destacamos o coeficiente numérico e a parte literal (formada por letras)
Exemplo
7x , coeficiente 7 e parte literal x
4/5a² coeficiente 4/5, parte literal a²
-5x²y coeficiente -5, parte literal x²y
-xyz coeficiente -1, parte literal xyz
Obs: todo o número real é um monômio sem parte literal
GRAU DE UM MONÔMIO
O grau de um monômio é dado pela soma dos expoentes de sua parte literal
Exemplo 1
Qual o grau do monômio 7x³y² ?
Solução:
Somando-se os expoentes dos fatores literais,temos 3 + 2 = = 5
resposta 5º
Exemplo 2
Qual o grau do monômio -8a²bc?
Solução:
Somando-se os expoentes dos fatores, temos: 2 + 1 + 1 = 4
resposta 4º grau
Observação:
O grau de um monômio também pode ser dado em relação a uma letra de sua parte literal.
Exemplo 3
7 x³y² - é de 3º grau em relação a x , é do 2º grau em relação a y
EXERCÍCIOS
1) De o grau de cada um dos seguintes monômios:
a) 5x² =
(R: 2º grau)
b) 4x⁵y³ =
(R: 8º grau)
c) -2xy² =
(R: 3º grau)
d) a³b² =
(R: 5º grau)
e) 7xy =
(R: 2º grau)
f) -5y³m⁴=
(R: 7º grau)
g) 6abc =
(R: 3º grau)
h) 9x³y²z⁵ =
(R: 10º grau)
POLINÔMIO COM UMA VARIÁRIAL
Polinômio é uma expressão algébrica de dois ou mais termos
Exemplos
1) 7x – 1
2) 8x² - 4x + 5
3) x³ + x² - 5x + 4
4) 4x⁵ - 2x³ + 8x² x + 7
Convém destacar que:
- Os expoentes da variável devem ser números naturais 1, 2, 3, 4, ......
- Os polinômios de dois termos são chamados binômios ( exemplo 1)
- Os polinômios de três termos são chamados trinômios (exemplo 2)
- Os polinômios com mais de três termos não tem nomes especiais. (exemplos 3 e 4)
GRAU DE UM POLINÔMIO A UMA VARIALVEL
O grau de um polinômio é indicado pelo maior expoente da variável
Exemplo
a) 7x⁴ - 3x² + 1 é um polinômio do 4º grau
b) x³ - 2x⁵ + 4 é um polinômio do 5º grau Em geral, os polinômios são ordenados segundo as potencias decrescentes da variáveis
Exemplos
5x³ + x⁴ + 6x – 7x² + 2 ( polinômio não ordenado)
x⁴ + 5x³ - 7x² + 6x + 2 ( polinômio ordenado)
Quando um polinômio estiver ordenado e estiver faltado uma ou mais potencias, dizemos que os coeficientes desses termos são zero e o polinômio é incompleto.
Exemplos
x⁴ + 5x + 1 ( polinômio incompleto)
x⁴ + 0x³ + 0x² + 5x + 1 (forma geral ou completa)
TERMOS SEMELHANTES
Dois ou mais termos são semelhantes quando têm a mesma parte literal
Exemplos
a) 5m e -7m são termos semelhantes
b) 2xy³ e 9y³x são termos semelhantes
Obs : não importa a ordem dos fatores literais Não são semelhantes os termos: 4x e 7x² observe que os expoentes de x são diferentes
EXERCICIOS
1) Quais pares de termos são sememlhantes?
a) 7a e 4a
(X)
b) 2x² e -6x²
(X)
c) 4y e 5y²
d) 8xy e –xy
(X)
e) 5a e 4ab
f) 4ab e 5/8 ab
(X)
g) 8xy e 5yx
(X)
h) 4x²y e –xy
i) xy² e 2x²y
j) 3acb e abc
(X)
REDUÇÃO DE TERMOS SEMELHANTES
Quando, numa mesma expressão, tivermos dois ou mais termos semelhantes podemos reduzi-los todos a um único termo, usando a propriedade distributiva
EXEMPLOS
1) 5x +3x – 2x = (5 + 3 – 2 )x = 6x
2) 7xy – xy + 5xy = (7 -1 + 5) xy = 11xy
Conclusão: somamos os coeficientes e conservamos a parte literal
EXERCÍCIOS
1) Reduza os termos semelhantes
a) 8a + 2a =
(R: 10a)
b) 7x – 5x =
(R: 2x)
c) 2y² - 9y² =
(R: -7y²)
d) 4a² - a² =
(R: 3a²)
e) 4y – 6y =
( -2y)
f) -3m² + 8m² =
(R: 5m²)
g) 6xy² - 8y²x =
(R: -2y²x)
h) 5a – 5a =
(R: 0)
2) Reduza os termos semelhantes:
a) 7x – 5x + 3x =
(R: 5x)
b) 2y – y – 10y =
(R: -9y)
c) 4a + a – 7a =
(R: -2a)
d) x² + x² - 2x² =
(R: 0 )
e) ab – ab + 5ab =
(R: 5ab)
f) 4x³ - x³ + 2x³ =
(R: 5x³)
g) 10x – 13x – x =
(R: -4x)
h) 8x – 10x + 4x =
(R: 2x)
3) Reduza os termos semelhantes:
a) 8x + 1x/2 =
(R: 17x/2)
b) 3a - 2a/3 =
(R: 7a/3)
c) 1x/2 + 1x/3 =
(R: 5x/6)
d) 2x/3 - 1x/2 =
(R: 1x/6)
e) 1y/2 – 2y/5 = (
R: 1y/10)
f) 2x + 1x/2 – 3x/4 =
(R: 7x/4)
Há casos em que numa expressão há termos diferentes e termos semelhantes entre si. Observe que a redução só pode ser feita com termos semelhantes.
Exemplo 1
7x + 8y – 2x – 5y
7x -2x + 8y -5y
5x + 3y
Exemplo 2:
4a³ + 5a² + 7a – 2a² + a³ - 9a + 6
4a³+ a³+ 5a²– 2a²+ 7a- 9ª + 6
5a³ + 3a² - 2a + 6
EXERCÍCIOS
1) Reduza os termos semelhantes:
a) 6a + 3a – 7 =
(R: 9a - 7)
b) 4a – 5 – 6a =
(R: -2a - 5)
c) 5x² + 3x² - 4 =
(R: 8x² - 4)
d) X – 8 + x =
(R: 2x -8)
e) 4m – 6m -1 =
(R: -2m -2)
f) 4a – 3 + 8 =
(R: 4a + 5)
g) x² - 5x + 2x² =
(R: 3x² - 5x)
h) 4a – 2m – a =
(R: 3a - 2m)
i) Y + 1 – 3y =
(R: -2y + 1)
j) X + 3xy + x =
(R : 3x + 3xy)
2) Reduza os termos semelhantes
a) 7a – 2a + 4b – 2b =
(R: 5a + 2b)
b) 5y² - 5x – 8y² + 6x =
(R: -3y² + 1x)
c) 9x² + 4x- 3x² + 3x =
(R: -6x² + 7x)
d) X + 7 + x – 10 – 1 =
(R: 2x -4)
e) x³ - x² + 7x² + 10x³ + 4 =
( -11x³ + 6x² + 4)
f) 2x³ - 7x² + 4x – 2 + 8 – 3x² = ( R:
g) 4a²b – 3b² - 6b² - 2a²b – 1 = (R:
3) Reduza os termos semelhantes
a) 1/2x – 1/3y + x=
b) 4a- 1/2a + 5 - 1/3 =
c) 1/2a- 3a² + a + 3a = 9ª – 6a²
d) 4y – 3/5y + 1/2 + 1 = 34y + 15
e) 2m + 3 + m/2 – ½ = 10m +10
ELIMINAÇÃO DE PARÊNTESES, COLCHETES E CHAVES
Vamos lembrar que:
1) Ao eliminar parênteses procedimentos pelo sinal positivo(+),não troque os sinais dos termos incluídos nos parênteses.
Exemplo
2x + (5x – 3)
2x + 5x – 3
7x – 3
2) Ao eliminar parênteses precedidos pelo sinal negativo ( - ), troque os sinais dos termos incluídos nos parênteses.
Exemplo
7x – (4x – 5)
7x – 4x + 5
3x + 5
Obs: Para a eliminação de colchetes e chaves são validas as regras acima.
Exemplos 1
5x + (3x -4) – (2x – 9)
5x +3x – 4 -2x + 9
5x + 3x -2x -4 + 9
6x + 5
Exemplo 2
8x – [-2x + (10 + 3x – 7)]
8x –[-2x +10+3x-7]
8x +2x -10-3x+7
8x + 2x – 3x -10 +7
7x -3
Exemplo 3
2x² + { 3x – [ 6x – ( 3x² + x)]}
2x² + { 3x – [ 6x – 3x² - x]}
2x² + { 3x – 6x + 3x² + x}
2x² + 3x – 6x + 3x² + x
2x² + 3x² + 3x -6x + x
5x² -2x
EXERCÍCIOS
1) Reduza os termos semelhantes nas seguintes expressões algébricas:
a) 6x + (2x – 4) – 2 =
(R: 8x – 6)
b) 7y -8 – (5y – 3) =
(R: 2y – 5)
c) 4x – ( -3x + 9 – 2x) =
(R: 9x – 9)
d) 3x – (-2x +5) – 8x + 9 =
(R: -3x + 4)
e) 4x – 3 + (2x + 1 ) =
(R: 6x – 2)
f) ( x + y ) – ( x + 2y) =
(R: -y)
g) (3x – 2y) + ( 7x + y) =
(R: 10x – y)
h) –(8x + 4) – ( 3x + 2) =
(R: -11x – 6)
2) Reduza os termos semelhantes nas seguintes expressões algébricas
a) 5x + ( 3x – 2) – ( 10x – 8) =
(R: -2x + 6)
b) 6x + (5x – 7) – (20 + 3x) =
(R: 8x -27)
c) ( x + y + z ) + x – ( 3y + z) =
(R: 2x – 2y)
d) (m + 2n ) – ( r - 2n ) – ( n + r) =
(R: m + 3n – 2r)
e) –(6y + 4x ) + ( 3y – 4x ) – ( -2x + 3y) =
(R: -6y – 6x)
3) Reduza os termos semelhantes nas seguintes expressões algébrica:
a) 6x² - [ 4x² + ( 3x – 5 ) + x =
(R: 2x² - 4x + 5)
b) 3x + { 2y – [ 5x – ( y + x )]} =
(R: -x + 3y)
c) -3x + [ x² - ( 4x² - x) + 5x] =
(R: -3x² + 3x)
d) Xy – [2x + ( 3xy – 4x ) + 7x ] =
(R: -2xy - 5x)
e) 8x – [( x + 2m) – ( 3x – 3m)] =
(R: 10x – 5m)
f) X – ( b – c) + [ 2x + ( 3b + c) ]=
(R: 3x + 2b + 2c )
g) –[x + ( 7 – x) – ( 5 + 2x) ]=
(R: -2x -2)
h) {9x – [ 4x – ( x – y ) – 5y ] + y} =
(R: 6x + 5y)
i) ( 3x + 2m) – [ (x – 2m) – ( 6x + 2m) ] =
(R: 8x + 6m)
j) 7x³ - { 3x² -x – [ 2x – ( 5x³ - 6x²) – 4x ]} =
(R: 2x³ + 3x² - x)
k) 2y – { 3y + [ 4y – ( y – 2x)+ 3x ] – 4x } + 2x =
(R: 11y – 4x)
l) 8y + { 4y – [ 6x – y – ( 4x – 3y ) – y ] -2x } =
(R: 6x + 4y)
m) 4x – { 3x + [ 4x – 3y – ( 6x – 5y ) – 3x ] – 6y }
n) 3x – { 3x – [ 3x – ( 3x –y ) – y ] –y } - y
4) Reduza os termos semelhantes:
a) -2n – (n – 8) + 1 =
(R: -3n + 9)
b) 5 – ( 2x – 5) + x =
(R: -x +10)
c) 3x + ( -4 – 6x) + 9 =
(R: -3x +5)
d) 8y – 8 – ( -3y + 5) =
(R: 11y – 13)
e) X – [ n + (x + 3) ] =
(R: -n -3)
f) 5 + [x – ( 3 – x) ] =
(R: 2x + 2)
g) x² - [ x – (5 - x²)] =
(R: -x + 5)
h) 5x – y – [x – (x - y)] =
(R: 5x – 2y)
5) Reduza os termos semelhantes:
a) 2x + ( 2x + y) – ( 3x – y) + 9x =
(R: 10x + 2y)
b) 5x – { 5x – [ 5x – ( 5x – m ) – m ] –m } – m =
(R: 0)
c) – { 7x – m – [ 4m – ( n – m – 3x) – 4x ] + n } =
(R: -8x + 6m -2n)
d) 5xy – { - (2xy + 5x )+ [3y – (-xy +x + 3xy)]} =
(R: 11xy + 6x - 3y)
http://jmpgeo.blogspot.com












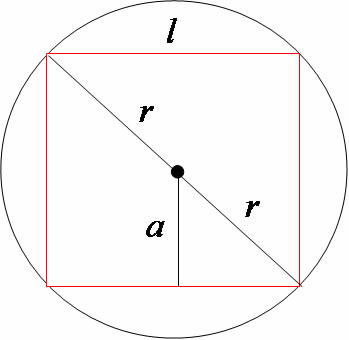
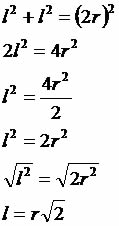

 fa= freqüência da fonte; vo= velocidade do observador; v = velocidade do som
fa= freqüência da fonte; vo= velocidade do observador; v = velocidade do som