Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Por volta do século XV, os matemáticos tinham um único pensamento: "O quadrado de um número positivo, bem como o de um número negativo, é positivo. Um número negativo não é quadrado de nenhum número, pois não existe raiz quadrada de um número negativo”.
Raízes quadradas de números negativos continuavam aparecendo, e o que mais preocupava os matemáticos da época era que essas raízes, sendo desenvolvidas de acordo com as regras algébricas, forneciam resultados satisfatórios, que não podiam ser obtidos de outra forma.
Foi através de estudos relacionados aos matemáticos Wessel, Argand e Gauss, que muitos resolveram associar os números a e b de um complexo a coordenadas de um ponto no plano, criando assim uma representação geométrica para um complexo.
A criação dos números complexos revolucionou, de certa forma, a Matemática, pois se criava mecanismos para obtenção de resultados envolvendo a raiz quadrada de um número negativo, até então um mistério. Os complexos são formados por uma parte real (x) e outra imaginária (y), assumindo a seguinte forma algébrica: z = x + yi. O número complexo pode ser representado no plano através de um ponto Q de coordenadas (x, y), sobre o eixo x marcamos a parte real e sobre o eixo y a parte imaginária de z. O ponto Q deve receber o nome de afixo ou imagem geométrica de z.
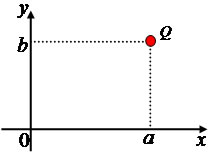
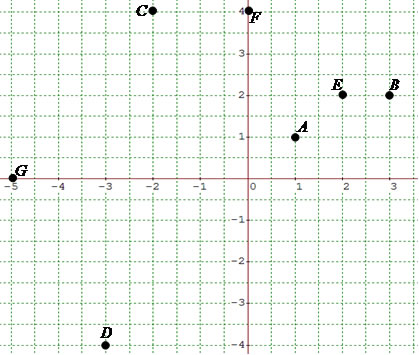
Representando geometricamente um número complexo
a) z = 1 + i, A(1,1)
b) z = 3 + 2i, B(3,2)
c) z = -2 + 4i, C(-2,4)
d) z = -3 -4i, D(-3,-4)
e) z = 2 + 2i, E(2,2)
f) z = 4i, F(0,4)
g) z = -5, G(-5,0)
Nenhum comentário:
Postar um comentário