Calculando a Diagonal do Quadrado e do Retângulo

Marcos Noé

Quadrados e retângulos

Os estudos relacionados à criação da Geometria e da Trigonometria datam dos séculos anteriores ao nascimento de Cristo. Naquela época, os grandes pensadores buscavam formas de elucidar situações matemáticas envolvendo a Geometria. Dentre esses inúmeros estudos surgiu um dos mais conhecidos e aplicáveis fundamentos da Matemática, o Teorema de Pitágoras.

Os primeiros passos rumo à criação do Teorema de Pitágoras ocorreram baseados no estudo do triângulo retângulo, em que Pitágoras estabeleceu uma relação entre os lados dessa figura de formato triangular. Os lados perpendiculares, isto é, que formam o ângulo de 90º (reto) foram denominados de catetos e o lado oposto ao ângulo reto foi chamado de hipotenusa.

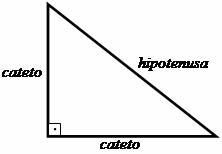
A relação proposta por Pitágoras sugere que: “A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.”

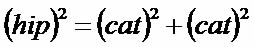
Essa relação utilizada para o cálculo das medidas de um dos lados do triângulo retângulo, também é utilizada para o cálculo das medidas de um quadrado ou retângulo. Nesses quadriláteros temos um elemento denominado diagonal, caracterizado por um segmento de reta responsável por unir dois vértices da figura. Observe os quadriláteros a seguir com destaque em relação a uma de suas diagonais.

Observe que ao traçarmos uma das diagonais dividimos o quadrilátero em dois triângulos retângulos, nos quais podemos aplicar o Teorema de Pitágoras para o cálculo das medidas desconhecidas.

Exemplo 1

Determine a medida da diagonal do seguinte quadrilátero.

A diagonal possui medida igual a 6√2 metros.


Exemplo 2

Uma casa possui a forma de um retângulo com medidas iguais a 14 metros de comprimento e 10 metros de largura. Determine a medida da diagonal dessa casa.

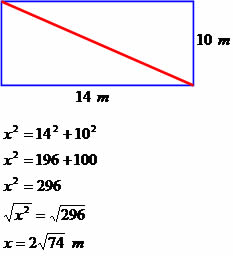
Diagonal medindo 2√74 metros.


Exemplo 3

Determine a medida do comprimento de uma região retangular com diagonal e largura medindo 50 e 30 metros, respectivamente.

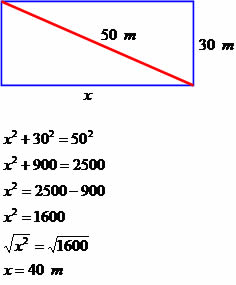
O comprimento possui medida equivalente a 40 metros.