Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
sexta-feira, 22 de maio de 2020
Coração
No homem, a circulação é feita através de um sistema fechado de vasos sanguíneos, cujo centro funcional é o coração.
O coração é um órgão musculoso oco, o miocárdio, com fibras estriadas, revestido externamente pelo pericárdio (serosa). O coração é do tamanho aproximado de um punho fechado e com peso em média de 400 g, tem cerca de 12 cm de comprimento por 8 a 9 cm de largura. O coração quase sempre continua a crescer em massa e tamanho até um período avançado da vida; este aumento pode ser patológico.
Localização e funcionamento
Ele se localiza no meio do peito, sob o osso esterno, ligeiramente deslocado para a esquerda. Ocupa no tórax, a região conhecida como mediastino médio. O coração funciona como uma bomba, recebendo o sangue das veias e impulsionando-o para as artérias.
Divisão do coração
O coração é dividido por um septo vertical em duas metades. Cada metade é formada de duas câmaras; uma aurícula superior e um ventrículo inferior. Entre cada câmara há uma válvula, a tricúspide do lado direito, e a bicúspide do lado esquerdo. Estas válvulas abrem-se em direção dos ventrículos, durante a contração das aurículas. Na aurícula direita chegam as veias cava superior e inferior, e na aurícula esquerda, as quatro veias pulmonares. Do ventrículo direito sai a artéria pulmonar e do ventrículo esquerdo sai a artéria aorta.

Estrutura e funções
A atividade do coração consiste na alternância da contração (sístole) e do relaxamento (diástole) das paredes musculares das aurículas e ventrículos. Durante o período de relaxamento, o sangue flui das veias para as duas aurículas, dilatando-as de forma gradual. Ao final deste período, suas paredes se contraem e impulsionam todo o seu conteúdo para os ventrículos.
A sístole ventricular segue-se imediatamente a sístole auricular. A contração ventricular é mais lenta e mais energética. As cavidades ventriculares se esvaziam quase que por completo com cada sístole, depois, o coração fica em um completo repouso durante um breve espaço de tempo. A freqüência cardíaca normal é de 72 batimentos por minuto, em situação de repouso.
Para evitar que o sangue, impulsionado dos ventrículos durante a sístole, reflua durante a diástole, há válvulas localizadas junto aos orifícios de abertura da artéria aorta e da artéria pulmonar, chamadas válvulas semilunares. Outras válvulas que impedem o refluxo do sangue são a válvula tricúspide, situada entre a aurícula e o ventrículo direito, e a válvula bicúspide ou mitral, entre a aurícula e o ventrículo esquerdo.
A freqüência das batidas do coração é controlada pelo sistema nervoso vegetativo, de modo que o simpático a acelera e o sistema parassimpático a retarda.
Doenças do coração
As doenças cardíacas são as principais causas de mortalidade nos países desenvolvidos. Podem ocorrer em conseqüência de defeitos congênitos, infecções, estreitamento das artérias coronárias, hipertensão ou alterações no ritmo cardíaco.
A principal forma de doença cardíaca nos países ocidentais é a arteriosclerose. O acúmulo de depósito de material lipídico - colesterol - pode causar uma obstrução que tampa as artérias (trombose). Esta é a causa mais importante de um ataque cardíaco, ou infarto do miocárdio, que tem conseqüências mortais com freqüência .
A alteração do ritmo cardíaco normal (arritmia) é a causa imediata de morte em muitos infartos do miocárdio.
O problema mais grave é o bloqueio cardíaco completo. Este pode ser corrigido pela implantação de um marcapasso artificial (um dispositivo que emite descargas elétricas rítmicas), para provocar a contração regular do músculo cardíaco.
Eletrocardiograma
Um Eletrocardiograma (ECG) registra a atividade elétrica do coração. Um impulso elétrico, gerado no nódulo sino-auricular, precede cada contração do músculo cardíaco; as ondas desenhadas em um ECG traçam o trajeto desses impulsos tal como se propagam no coração. As irregularidades do ECG refletem afecções no músculo, no fornecimento de sangue ou no controle neural do coração
www.colaweb.com
O coração é um órgão musculoso oco, o miocárdio, com fibras estriadas, revestido externamente pelo pericárdio (serosa). O coração é do tamanho aproximado de um punho fechado e com peso em média de 400 g, tem cerca de 12 cm de comprimento por 8 a 9 cm de largura. O coração quase sempre continua a crescer em massa e tamanho até um período avançado da vida; este aumento pode ser patológico.
Localização e funcionamento
Ele se localiza no meio do peito, sob o osso esterno, ligeiramente deslocado para a esquerda. Ocupa no tórax, a região conhecida como mediastino médio. O coração funciona como uma bomba, recebendo o sangue das veias e impulsionando-o para as artérias.
Divisão do coração
O coração é dividido por um septo vertical em duas metades. Cada metade é formada de duas câmaras; uma aurícula superior e um ventrículo inferior. Entre cada câmara há uma válvula, a tricúspide do lado direito, e a bicúspide do lado esquerdo. Estas válvulas abrem-se em direção dos ventrículos, durante a contração das aurículas. Na aurícula direita chegam as veias cava superior e inferior, e na aurícula esquerda, as quatro veias pulmonares. Do ventrículo direito sai a artéria pulmonar e do ventrículo esquerdo sai a artéria aorta.

Estrutura e funções
A atividade do coração consiste na alternância da contração (sístole) e do relaxamento (diástole) das paredes musculares das aurículas e ventrículos. Durante o período de relaxamento, o sangue flui das veias para as duas aurículas, dilatando-as de forma gradual. Ao final deste período, suas paredes se contraem e impulsionam todo o seu conteúdo para os ventrículos.
A sístole ventricular segue-se imediatamente a sístole auricular. A contração ventricular é mais lenta e mais energética. As cavidades ventriculares se esvaziam quase que por completo com cada sístole, depois, o coração fica em um completo repouso durante um breve espaço de tempo. A freqüência cardíaca normal é de 72 batimentos por minuto, em situação de repouso.
Para evitar que o sangue, impulsionado dos ventrículos durante a sístole, reflua durante a diástole, há válvulas localizadas junto aos orifícios de abertura da artéria aorta e da artéria pulmonar, chamadas válvulas semilunares. Outras válvulas que impedem o refluxo do sangue são a válvula tricúspide, situada entre a aurícula e o ventrículo direito, e a válvula bicúspide ou mitral, entre a aurícula e o ventrículo esquerdo.
A freqüência das batidas do coração é controlada pelo sistema nervoso vegetativo, de modo que o simpático a acelera e o sistema parassimpático a retarda.
Doenças do coração
As doenças cardíacas são as principais causas de mortalidade nos países desenvolvidos. Podem ocorrer em conseqüência de defeitos congênitos, infecções, estreitamento das artérias coronárias, hipertensão ou alterações no ritmo cardíaco.
A principal forma de doença cardíaca nos países ocidentais é a arteriosclerose. O acúmulo de depósito de material lipídico - colesterol - pode causar uma obstrução que tampa as artérias (trombose). Esta é a causa mais importante de um ataque cardíaco, ou infarto do miocárdio, que tem conseqüências mortais com freqüência .
A alteração do ritmo cardíaco normal (arritmia) é a causa imediata de morte em muitos infartos do miocárdio.
O problema mais grave é o bloqueio cardíaco completo. Este pode ser corrigido pela implantação de um marcapasso artificial (um dispositivo que emite descargas elétricas rítmicas), para provocar a contração regular do músculo cardíaco.
Eletrocardiograma
Um Eletrocardiograma (ECG) registra a atividade elétrica do coração. Um impulso elétrico, gerado no nódulo sino-auricular, precede cada contração do músculo cardíaco; as ondas desenhadas em um ECG traçam o trajeto desses impulsos tal como se propagam no coração. As irregularidades do ECG refletem afecções no músculo, no fornecimento de sangue ou no controle neural do coração
www.colaweb.com
Fração e decimais
NÚMEROS FRACIONÁRIOS E DECIMAIS
Durante muito tempo, os números naturais eram os únicos números que o homem utilizava. Mas, com o passar do tempo, o homem foi encontrando situações mais difíceis para resolver. No antigo Egito, por exemplo, as terras próximas ao rio Nilo eram muito disputadas por isso os faraós tinham funcionários que mediam e demarcavam os terrenos.
Eles usavam cordas com nós separados sempre pela mesma distância. Em muitos casos, principalmente para efetuar medições, precisou criar outros números que não fossem apenas os números naturais. Surgiram assim, os números fracionários ou racionais.
Para representar os números fracionários foi criado um símbolo, que é a fração. Sendo a e b números racionais e b ≠ 0, indicamos a divisão de a por b com o símbolo a : b ou, ainda a/b
Chamamos o símbolo a/b de fração.
Assim, a fração 10/2 é igual a 10 : 2
Na fração a/b, a é o numerador e b é o denominador
Efetuando, por exemplo, a divisão de 10 por 2, obtemos o quociente 5.
Assim, 10/2 é um número natural, pois 10 é múltiplo de 2.
Mas efetuando a divisão de 3 por 4 não obtemos um número natural. Logo ¾ não é um número natural. A fração envolve a idéia de alguma coisa que foi dividida em partes iguais.
Agenor comeu ¾ de uma barra de chocolate. Que quantidade de chocolate Agenor comeu? Que parte da barra de chocolate sobrou?
Dividindo o chocolate em 4 partes, iguais temos;
Agenor comeu ¾ , portanto sobrou ¼
LEITURA DE UMA FRAÇÃO
Algumas frações recebem nomes especiais: as que têm denominadores 2,3,4,5,6,7,8,9
½ um meio
¼ um quarto
1/6 um sexto
1/8 um oitavo
2/5 dois quintos
9/8 nove oitavos
1/3 um terço
1/5 um quinto
1/7 um sétimo
1/9 um nono
4/9 quatro nonos
16/9 dezesseis nonos
as que tem denominadores 10, 100, 1000, etc.............
1/10 um décimo
1/100 um centésimo
1/1000 um milésimo
7/100 sete centésimos
as decimais que são lidas acompanhadas da palavra avos :
1/11 um onze avos
7/120 sete cento e vinte avos
4/13 quatro treze avos
1/300 um trezentos avos
5/19 cinco dezenove avos
6/220 seis duzentos e vinte avos
EXERCÍCIOS
1) indique as divisões em forma de fração:
a) 14 : 7 = (R: 14/7)
b) 18 : 8 = (R: 18/8)
c) 5 : 1 = (R: 5/1)d) 15 : 5 = ( R: 15/5)
e) 18 : 9 = (R: 18/9)
f) 64 : 8 = (R: 64/8)
2) Calcule o quociente das divisões
a) 12/3 = (R:4)
b) 42/21 = (R: 2)
c) 8/4 = (R: 2)d) 100/10 = (R: 10)
e) 56/7 = (R: 8)
f) 64/8 = (R: 8 )
3) Em uma fração, o numerador é 5 e o denominador é 6
a) Em quantas partes o todo foi dividido? (R: 6)b) Quantas partes do todo foram consideradas? (R: 5)
4) Escreva como se lêem as seguintes frações:
a) 5/8 (R: cinco oitavos)b) 9/10 (R: nove décimos)
c) 1/5 (R: um quinto)
d) 4/200 ( R: quatro duzentos avos)
e) 7/1000 (R: sete milésimos)
f) 6/32 (R: seis trinta e dois avos)
TIPOS DE FRAÇÕES
a) Fração própria : é aquela cujo o numerador é menor que o denominador.
Exemplos : 2/3, 4/7, 1/8
b) Fração imprópria: é a fração cujo numerador é maior ou igual ao denominador
Exemplo: 3/2, 5/5
c) Fração aparente: é a fração imprópria cujo o numerador é múltiplo do denominador
Exemplo: 6/2, 19/19, 24/12, 7/7
EXERCÍCIO
1) Classifique as frações em própria, imprópria ou aparente:
a) 8/9 (R: própria)
b) 10/10 (R: imprópria e aparente)
c) 26/13(R: imprópria e aparente)
d) 10/20 (R: própria)
e) 37/19 (R: imprópria)
f) 100/400 (R: própria)
FRAÇÕES EQUIVALENTES
Para encontrar frações equivalentes, multiplicamos o numerador e o denominador da fração ½ por um mesmo numero natural diferente de zero.
Assim: ½, 2/4, 4/8, 3/6, 5/10 são algumas frações equivalentes a 1/2
SIMPLIFICANDO FRAÇÕES
Cláudio dividiu a pizza em 8 partes iguais e comeu 4 partes. Que fração da pizza ele comeu?
Cláudio comeu 4/8 da pizza. Mas 4/8 é equivalente a 2/4. Assim podemos dizer que Cláudio comeu 2/4 da pizza.
A fração 2/4 foi obtida dividindo-se ambos os termos da fração 4/8 por 2 veja:
4/8 : 2/2 = 2/4
Dizemos que a fração 2/4 é uma fração simplificada de 4/8.
A fração 2/4 ainda pode ser simplificada, ou seja, podemos obter uma fração equivalente dividindo os dois termos da fração por 2 e vamos obter ½
OPERAÇÕES COM NÚMEROS RACIONAIS ABSOLUTOS (FRAÇÕES)
ADIÇÃO E SUBTRAÇÃO
1°) Como adicionarmos ou subtrairmos números fracionários escritos sob a forma de fração de denominadores iguais
Conclusão: Somamos os numeradores e conservamos o denominador comum.
Exemplo:
a) 5/7 – 2/7 = 3/7
b) 4/9+ + 2/9 = 6/9 = 2/3
c) 3/5 – 1/5 = 2/5
Exercícios
1) Efetue as adições
a) 3/6 + 2/6 = (R: 5/6)b) 13/7 + 1/7 = (R: 14/7)
c) 2/7+ 1/7 + 5/7 = (R: 8/7)d) 4/10 + 1/10 + 3/10 = (R: 8/10)
e) 5/6 + 1/6 = (R: 1)
f) 8/6 + 6/6 = (R: 14/6) = (R: 7/3)
g) 3/5 + 1/5 = (R: 4/5)
2) Efetue as subtrações:
a) 7/9 – 5/9 = (R: 2/9)
b) 9/5 -2/5 = (R: 7/5)
c) 2/3 – 1/3 = (R: 1/3)
d) 8/3 – 2/3 = (R: 6/3)
e) 5/6 – 1/6 = (R: 2/3)
f) 5/5 – 2/5 = (R: 3/5)
g) 5/7 – 2/7 = (R: 3/7)
3) Efetue as operações:
a) 5/4 + ¾ - ¼ = (R: 7/4)
b) 2/5 + 1/5 – 3/5 = (R: 0/5)
c) 8/7 – 3/7 + 1/7 = (R: 6/7)d) 7/3 – 4/3 – 1/3 = (R: 2/3)
e) 1/8 + 9/8 -3/8= (R: 7/8)
f) 7/3 – 2/3 + 1/3 = (R:6/3 ) = (R: 2)
g) 7/5 + 2/5 – 1/5 = (R: 8/5)
h) 5/7 – 2/7 – 1/7 = (R: 2/7)
2°) Como adicionarmos ou subtrairmos números fracionários escritos sob a forma de fração de denominadores diferentes
conclusão: Quando os denominadores são diferentes fazemos o m.m.c. dos denominadores .
exemplo:
a) 2/3 +1/2 = 4/6 + 3/6 = 7/6
3, 2 I 2
3, 1 I 3
1, 1 I ---2 . 3 = 6
b) 2/3 – ¼ = 8/12 – 3/12 = 5/12
3, 4 I 2
3, 2 I 2
3, 1 I 3
1, 1 I ----2 . 2. 3 = 12
exercícios
1) Efetue as adições:
a) 1/3 + 1/5 = (R: 8/15)
b) ¾ + ½ = (R: 5/4)
c) 2/4 + 2/3 = (R: 14/12)
d) 2/5 + 3/10 = (R: 7/10)
e) 5/3 + 1/6 = (R: 11/6)
f) ¼ + 2/3 + ½ = (R: 17/12)
g) ½ + 1/7 + 5/7 = (R: 19/14)
h) 3/7 + 5/2 + 1/14 = (R: 42/14)
i) 4/5 + 1/3 + 7/6 = (R: 69/30)
j) 1/3 + 5/6 + ¾ = (R: 23/12)
k) ½ + 1/3 + 1/6 = (R: 1)l) 10 + 1/8 + ¾ = (R: 85/8)
m) 1/3 + 3/5 = (R:14/15)
n) ¾ + 6/7 = (R: 45/28)
o) 5/7 + ½ = (R: 17/14)
p) ½ + 1/3 = (R: 5/6)
q) 3/14 + 3/7 = (R: 9/14)
r) 3/5 + ¾ + ½ = (R: 37/20)
s) 1/12 + 5/6 + ¾ = (R: 20/12)
t) 8 + 1/5 + 4/5 = (R: 45/5)
u)
2) efetue as subtrações
a) 5/4 – ½ = (R: 3/4)
b) 3/5 – 2/7 = (R: 11/35)
c) 8/10 – 1/5 = (R: 6/10)
d) 5/6 – 2/3 = (R: 1/6)
e) 4/3 – ½ = (R: 5/6)
f) 13/4 – 5/6 = (R: 29/12)
g) 7/8 – 1/6 = (R: 17/24)
h) 4/5 – 1/3 = (R: 7/15)
i) 3/5 – ¼ = (R: 7/20)
j) 10/11 – ½ = (R: 9/22)
l) 6/4 – 2/3 = (R: 10/12)
m) 5/8 – ½ = (R: 1/8)
n) 4/5 – ¼ = (R: 11/20)
o) ¾ - 5/8 = (R: 1/8)
p) 9/11 – ½ = (R: 7/22)
q) 7 – 2/3 = (R: 19/3)r) 4/2 - 2/3 = (R: 8/6)
s) 3/2 - 2/3 = (R: 5/6)
t) 1/2 - 1/3 = (R: 1/6)
u) 3/2 - 1/4 = (R: 5/4)
3) Efetue
a) 2 + 5/3 = (R: 11/3)
b) 7 + ½ = (R: 15/2)
c) 3/5 + 4 = (R: 23/5)
d) 6/7 + 1 = (R: 13/7)
e) 8 + 7/9 = (R: 79/9)
f) 5 – ¾ = (R: 17/4)
g) 2 – ½ = (R: 3/2)
h) 7/2 – 3 = (R: 1/2)
i) 11/2 – 3 = (R: 5/2)
j) 7/4 – 1 = (R: 3/4)
k) 1 – ¼ = (R: ¾ )
l) ½ - 1/3 = (R: 1/6)
m) ½ + ¼ = (R: ¾)
n) 1 + 1/5 = (R: 6/5)
o) 1 – 1/5 = (R: 4/5)
4) Calcule o valor das expressões:
a) 3/5 + ½ - 2/4 = (R: 12/20)
b) 2/3 + 5/6 – ¼ = (R: 15/12)c) 4/5 – ½ + ¾ = (R: 21/20)
d) 5/7 – 1/3 + ½ = (R: 37/42)
e) 1/3 + ½ - ¼ = (R: 7/12)
f) ¾ - ½ + 1/3 = (R: 7/12)
g) 5/6 – ½ + 2/3 = (R: 1)
h) 4/5 – ¾ + ½ = (R: 11/20)
i) ½ + 2/3 + 2/5 + 1/3 = (R: 57/30)
j) 6/5 – ¾ + ½ - 2/3 = (R: 17/60)l) 1/6 + 5/4 + 2/3 = (R: 25/12)
MULTIPLICAÇÃO
Vamos Calcular : 2/3 x 4/5 = 8/15
Conclusão : multiplicamos os numeradores entre si e os denominadores entre si
Exemplo:
a) 4/7 x 3/5 = 12/35
b) 5/6 x 3/7 = 15//42 = 5/14 simplificando
EXERCICIOS
1) Efetue as multiplicações
a) ½ x 8/8 = (R: 8/16)
b) 4/7 x 2/5 = (R: 8/35)
c) 5/3 x 2/7 = (R: 10/21)
d) 3/7 x 1/5 = (R: 3/35)
e) 1/8 x 1/9 = (R: 1/72)
f) 7/5 x 2/3 = (R: 14/15)
g) 3/5 x ½ = (R: 3/10)h) 7/8 x 3/2 = (R: 21/16)
i) 1/3 x 5/6 = (R: 5/18)
j) 2/5 x 8/7 = (R: 16/35)k) 7/6 x 7/6 = (R: 49/36)
l) 3/7 x 5/2 = (R: 15/14)
m) 3/10 x 5/9 = (R: 15/90)
n) 2/3 x ¼ x 5/2 = (R: 10/24)
o) 7 x ½ x 1/3 = (R: 7/6)
p)
2) Efetue as multiplicações
a) 4/3 x ½ x 2/5 = (R: 8/30)
b) 1/5 x ¾ x 5/3 = (R: 15/60)
c) ½ x 3/7 x 1/5 = (R: 3/70)d) 3/2 x 5/8 x ¼ = (R: 15/64)
e) 5/4 x 1/3 x 4/7 = (R: 20/84)
3) Efetue as multiplicações
a) 2 x 5/3 = (R: 10/3)
b) 3 x 2/5 = (R: 6/5)
c) 1/8 x 5 = (R: 5/8)d) 6/7 x 3 = (R: 18/7)e) 2 x 2/3 x 1/7 = (R: 4/21)
f) 2/5 x 3 x 4/8 = (R: 24/40)
g) 5 x 2/3 x 7 = (R: 70/3)
h) 7/5 x 2 x 4 = (R: 56/5)
i) 8 x 2/3 = (R: 16/3)
j) 5/9 x 0/6 = (R: 0/54)
k) 1/7 x 40 = (R: 40/7)l) ½ x 1/3 x ¼ x 1/5 = (R: 1/120)m) 1 x 2/3 x 4/3 x 1/10 = (R: 8/90)
DIVISÃO
Vamos calcular ½ : 1/6
Para dividir uma fração por outra, basta multiplicar a primeira fração pela inversa da segunda
Assim: ½ : 1/6 = ½ x 6/1 = 6/2 = 3
Exemplos:
a) 2/3 : 5/2 = 2/3 x 2/5 = 4/15
b) 7/9 : 1/5 = 7/9 x 5/1 = 35//9
c) 3/7 : 4 = 3/7 x ¼ = 3/28
Exercícios
1) Efetue as divisões
a) ¾ : 2/5 = (R: 15/8)
b) 5/7 : 2/3 = (R: 15/14)
c) 4/5 : 3/7 = (R: 28/15)
d) 2/9 : 7/8 = (R: 16/63)
e) 1/6 : 5/3 = (R: 3/30) ou (3/10)
f) 7/8 : ¾ = (R: 28/24) ou (7/6)g) 8/7 : 9/3 = (R: 24/63)
h) 4/5 : 2/5 = (R: 20/10) ou (2/1) ou ( 2)i) 5/8 : ¾ = (R: 20/24) ou (5/6)
j) 2/9 : 4/7 = (R: 14/36) ou (7/18)
2) Efetue as divisões :
a) 5 : 2/3 = (R: 15/2)
b) 4 : 1/7 = (R: 28/1) ou (28)
c) 8/9 : 5 = (R: 8/45)
d) 3/7 : 3 = (R: 3/21)
e) 7/3 : 4/7 = (R: 49/12)
f) 2/3 : ½ = (R: 4/3)
g) 4/5 : 2/3 = (R: 12/10)
h) 2/7 : 5/3 = (R: 6/35)
i) 3/7 : 2 = (R: 3/14)
j) 3/2 : 5/7 = (R: 21/10)
k) 3/8 : 4/7 = (R: 21/32)
POTENCIAÇÃO
Vamos calcular a potência (2/5)³= 2/5 x 2/5 x 2/5 = 8/125
Conclusão: para elevar uma fração a um expoente, elevam-se o numerador e o denominador da fração desse expoente.
Exemplo
a) (5/7)² = 5²/ 7² = 25/49
1) Toda fração de expoente 1 dá como resultado a própria fração
Exemplo: (3/8)¹ = 3/8
2) Toda a fração elevada ao expoente zero dá como resultado o número 1
Exemplo : (3/4)⁰ = 1
Exercícios
1) Calcule as potências
a) (2/3)² = (R: 4/9)
b) (4/7)² = (R: 16/49)
c) (7/5)² = (R: 49/25)
d) (1/3)² = (R: 1/9)
e) (5/3)² = (R: 25/9)
f) (7/30)⁰ = ( R: 1)
g) (9/5)¹ = (R: 9/5)
h) (2/3)³ = (R: 8/27)
i) (1/5)³ = (R: 1/125)
j) (1/2)² = (R: 1/4)
k) (2/3)⁴= (R: 16/81)
l) (2/5)¹ = (R: 2/5)
m) (3/11)² = (R: 9/121)
n) (9/4)⁰ = (R: 1)o) (12/13)² = (R: 144/169)
p) (1/2)⁵ = (R: 1/32)q) (3/7)³ = ( R: 27/343)
RAIZ QUADRADA DE NÚMEROS RACIONAIS (FRAÇÃO)
Sabemos que :
√25 = 5
√49 = 7
√25/49 = 5/7
Conclusão:
Para extrair a raiz quadrada de um número fracionário, extraem-se a raiz quadrada do numerador e a raiz quadrada do denominador.
Exemplos
a) √4/9 = 2/3
b) √1/36 = 1/6
Exercícios
1) Calcule a raiz quadrada
a) √9/16 = (R: 3/4)
b) √1/25 = (R:1/5)
c) √9/25 = (R: 3/5)
d) √16/49 = (R: 4/7)
e) √64/25 = (R: 8/5)
f) √1/9 = (R: 1/3)
g) √25/81 = (R: 5/9)
h) √49/36 = (R: 7/6)
i) √1/100 = (R: 1/10)
EXPRESSÕES COM NÚMEROS RACIONAIS
As expressões com números racionais devem ser resolvidas obedecendo à seguinte ordem de operações:
1°) Potenciação e Radiciação
2°) Multiplicação e Divisão
3°) Adição e subtração
Essas operações são realizadas eliminando :
1°) Parênteses
2°) Colchetes
3°) Chaves
exemplos:
1) 1/5 + 4/5 x 1/3 =
1/5 + 4/15 =
3/15 + 4/15 =
7/15
2) (3/5)² + 2/5 x ½ =
9/25 + 2/10 =
18/50 + 10/50 =
= 28/50 = 14/25
3) ( 4 + ½ ) – 1/5 : 2/3 =
( 8/2 + ½ ) – 1/5 : 2/3 =
9/2 – 1/5 : 2/3 =
9/2 – 1/5 x 3/2 =
9/2 – 3/10 =
45/10 – 3/10 =
= 42/10 = 21/5
Exercícios
1) Calcule o valor das expressões:
a) 5/8 + ½ -2/3 = (R: 11/24)
b) 5 + 1/3 -1/10 = (R: 157/30)
c) 7/8 – ½ - ¼ = (R: 1/8)
d) 2/3 + 3 + 1/10 = (R: 113/30)
e) ½ + 1/6 x 2/3 = (R: 11/18)
f) 3/10 + 4/5 : ½ = (R: 19/10)
g) 2/3 x ¾ - 1/6 = (R: 4/12 ou 1/3)
h) 7 – ¼ + 1/7 = (R: 193/28)
i) 3 x ½ - 4/5 = (R: 7/10)
j) 7/4 – ¼ x 3/2 = ( R: 11/8)k) ½ + 3/2 x ½ = ( R: 5/4)
l) 1/10 + 2/3 x ½ = (R: 13/30)
2) Calcule o valor da expressão:
a) 7 x ½ + (4/5)² = (R: 207/50)
b) (1/3)² + 2/5 x ½ = (R: 28/90 ) ou (14/45)
c) (1/2)² : ¾ + 5/3 = ( R: 24/12) ou (2)d) (1/3)² x 5/2 + ½ = ( R: 14/18) ou (7/9)
e) 2/5 x ½ + ( 3/5)² = ( R: 28/50) ou (14/25)f) (2/3)²+ 4 + 1/3 -1/2 = ( R: 77/18)
3) Calcule o valor da expressão:
a) 5/6 – ( 1/3 + 1/5 ) = ( R: 9/30) ou (3/10)
b) 2/5 x ( ¾ + 5/8) = ( R: 22/40) ou (11/20)c) ½ : ( 2/3 + ¾ ) = ( R: 12/34) ou ( 6/17)
d) ( 1/3 + ½ ) : 5/6 = (R: 30/30) ou (1)
e) ½ . ( 2/3 + ¾ ) = ( R: 17/24)f) ( 5/7 x 2/3 ) : 1/6 = (R: 60/21)
g) (3/2 - 2/5 ) + ( 5/4 - 2/3) = (R: 101/60)
h) 1 + (1/2 - 1/5) - (7/4 - 5/4) = (R: 16/20)i) ( 7/8 - 5/6) + ( 8/9 - 7/9) = (R: 11/72)
4) Calcule o valor das expressões
a) ( ¾ x ½ + 2/5 ) + ¼ = (R: 41/40)b) ( 2/3 x ¼ ) + ( 1/3 x ½ ) = (R: 4/12)
c) ( 5- ½ ) : ( 2 – 1/3) = ( R: 27/10)d) ( 3 x 5/2 ) : ( 1/5 + 1/3 ) = (R: 225/16)
e) ( 3 x ¾ ) + ( 3 x ¼ ) = ( R: 12/4)
f) ( 3 + ½ ) x 4/5 – 3/10 = (R: 25/10)
5) Calcule o valor das expressões
a) ½ : 1/3 + ¾ x 5/9 = ( R: 69/36)
b) 3/8 x ( ½ x 4/3 + 4/3 ) = (R: 36/48)
c) ( 1/3 + ¼ ) : 5/2 + 2/3 = (R: 54/60)
d) ( ¾ + ¼ - ½ ) : 3/2 = (R: 8/11)
d) ( 1 + 1/3 )² x 9/4 + 6 = (R: 360/36)
e) 1 + (3/2)² + ( 1 + ¼ ) = (R: 18/4)
6) calcule o valor das expressões
PROBLEMAS COM NÚMEROS RACIONAIS
Os problemas com números racionais absolutos são geralmente resolvidos da seguinte forma :
1°) Encontrando o valor de uma unidade fracionária
2°) obtendo o valor correspondente da fração solicitada
exemplo
Eu tenho 60 fichas, meu irmão tem ¾ dessa quantidade. Quantas fichas tem o meu irmão ?
60 x ¾ = 180/4 = 45
R: O meu irmão tem 45 fichas
EXERCICIOS
1) Determine 2/3 de R$ 1200,00 (R: 800)
2) Numa caixa existem 80 bombons. Calcule 2/5 desses bombons. (R: 32)
3) O comprimento de uma peça de tecido é de 42 metros. Quanto medem 3/7 dessa peça ? (R: 18 m)
4) Um automóvel percorreu 3/5 de uma estrada de 600 km. Quantos quilômetros percorreu? (R: 360 km)
5) Numa viagem de 72 km, já foram percorridos ¾ . Quantos quilômetros já foram percorridos? (R : 54 km)
6) Um livro tem 240 páginas., Você estudou 5/6 do livro. Quantas paginas você estudou? (R: 200)
7) Os 2/5 de um número correspondem a 80. Qual é esse número? (R: 200)
8) Os ¾ do que possuo equivalem a R$ 900,00. Quanto possuo? (R: 1200)
9) Um time de futebol marcou 35 gols, correspondendo a 7/15 do total de gols do campeonato. Quantos gols foram marcados no campeonato? (R: 75)
10) Para encher 1/5 de um reservatório são necessários 120 litros de água. Quanto é a capacidade desse reservatório? (R: 600 litros)
11) Se 2/9 de uma estrada corresponde a 60 km, quantos quilômetros tem essa estrada?
(R: 270 km)
12) Para revestir ¾ de uma parede foram empregados 150 azulejos. Quantos azulejos são necessários para revestir toda a parede? (R: 200)
13) De um total de 240 pessoas,1/8 não gosta de futebol. Quantas pessoas gostam de futebol?
(R: 210)
14) Eu fiz uma viagem de 700 km. Os 3/7 do percurso foram feitos de automóvel e o restante de ônibus. Que distancia eu percorri de ônibus? (R: 400 km)
15) Numa prova de 40 questões um aluno errou ¼ da prova. Quantas questões ele acertou?
(R: 30 )
16) Numa classe de 45 alunos, 3/5 são meninas. Quantos meninos há nessa classe? (R: 18)
17) Um brinquedo custou R$ 152,10,. Paguei 1/6 do valor desse objeto. Quanto estou devendo?
(R: 126,75)
NÚMEROS DECIMAIS
FRAÇÃO DECIMAL
Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100...
como:
a) 7/10
b) 3/100
c) 27/1000
NÚMEROS DECIMAIS
a) 7/10 = 0,7
b) 3/100 = 0,03
c) 27/1000 = 0,027
nos números decimais , a virgula separa a parte inteira da parte decimal
LEITURA DO NÚMERO DECIMAL
Para ler um, número decimal, procedemos do seguinte modo:
1°) Lêem -se os inteiros
2°) Lê-se a parte decimal, seguida da palavra:
décimos - se houver uma casa decimal
centésimos - se houver duas casas decimais
milésimos - se houver três casas decimais
exemplos:
a) 5,3 - lê-se cinco inteiros e três décimos
b) 1,34 - lê-se um inteiro e trinta e quatro centésimos
c) 12,007 - lê-se doze inteiros e sete milésimos
quando a parte inteira for zero, lê-se apenas a parte decimal
a) 0,4 - lê-se quatro décimos
b) 0,38 - lê-se trinta e oito centésimos
TRANSFORMAÇÃO DE FRAÇÃO DECIMAL EM NÚMERO DECIMAL
Para transformar uma fração decimal em número decimal, escrevemos o numerador e separamos, à direita da virgula, tantas casas quanto são os zeros do denominador
exemplos:
a) 42/10 = 4,2
b) 135/100 = 1,35
c) 135/1000 = 0,135
Quando a quantidade de algarismos do númerador não for suficiente para colocar a vírgula, acrescentamos zeros à esquerda do número.
exemplo:
a) 29/1000 = 0,029
b) 7/1000 = 0,007
EXERCÍCIOS ,
1) transforme as frações em números decimais
a) 3/10 = (R: 0,3)
b) 45/10 = (R: 4,5)
c) 517/10 = (R:51,7)
d) 2138/10 = (R: 213,8)
e) 57/100 = (R: 0,57)f) 348/100 = (R: 0,348)
g) 1634/100 = (R: 1,634)
h) 328/ 1000 = (R: 0,328)
i) 5114 / 1000 = (R: 5,114)
j) 2856/1000 = (R: 2,856)l) 4761 / 10000 = (R: 0,4761)
m) 15238 /10000 = (R: 1,5238)
2) transforme as frações em números decimais
a) 9 / 100 = (R: 0,09)
b) 3 / 1000 = (R: 0,003)c) 65 /1000 = (R: 0,065)d) 47 /1000 = (R: 0,047)e) 9 / 10000 = (R: 0,0009)f) 14 / 10000 = (R: 0,0014)
TRANSFORMAÇÃO DE NÚMERO DECIMAL EM FRAÇÃO
Procedimentos:
1) O numerador é um número decimal sem a virgula
2) O denominador é o número 1 acompanhado de tantos zeros quantos forem os algarismos do número decimal depois da vírgula.
exemplos:
a) 0,7 = 7/10
b) 8,34 / 834 /100
0,005 = 5/ 1000
EXERCÍCIOS
1) Transforme os números decimais em frações
a) 0,4 = (R: 4/10)b) 7,3 = (R: 73/10)
c) 4,29 = (R: 429/100)
d) 0,674 = (R: 674/1000)
e) 8,436 = (R: 8436/1000)f) 69,37 = (R: 6937/100)
g) 15,3 = (R: 153/10)
h) 0,08 = (R: 8/100)
i) 0,013 = (R: 13/1000)j) 34,09 = (R: 3409/100)l) 7,016 = (R: 7016/1000)m) 138,11 = (R: 13811/100)
OPERAÇÕES COM NÚMEROS DECIMAIS
ADIÇÃO E SUBTRAÇÃO
Colocamos vírgula debaixo de vírgula e operamos como se fossem números naturais>
exemplo
1) Efetuar 2,64 + 5,19
2,64
5,19 +
----
7,83
2) Efetuar 8,42 - 5,61
8,42
5,61 -
----
2,81
Se o número de casas depois da virgula for diferente, igualamos com zeros à direita
3) Efetuar 2,7 + 5 + 0,42
2,70
5,00 +
0,42
----
8,12
4) efetuar 4,2 - 2,53
4,20
2,53 -
------
1,67
EXERCÍCIOS
1) Calcule
a) 1 + 0,75 = (R: 1,75)b) 0,8 + 0,5 = (R: 1,3)c) 0,5 + 0,5 = (R: 1,0)d) 2,5 + 0,5 + 0,7 = (R: 3,7)e) 0,5 + 0,5 + 1,9 + 3,4 = (R:6,3)
f) 5 + 0,6 + 1,2 + 15,7 = (R: 22,5)
2) Efetue as adições
a) 3,5 + 0,12 = (R: 3,62)
b) 9,1 + 0,07 = (R: 9,17)
c) 4,7 + 12,01 = (R: 16,71)
d) 2,746 + 0,92 = (R: 3,666)
e) 6 + 0,013 = (R: 6,013)f) 4 + 0,07 + 9,1 = (R: 13,17)g) 16.,4 + 1,03 + 0,72 = (R: 18,15)h) 5,3 + 8,2 + 0,048 = (R: 13,548)
i) 0,45 + 4,125 + 0,001 = (R: 4,576)
3) Efetue as subtrações
a) 8,2 - 1,7 = (R: 6,5)b) 5 - 0,74 = (R: 4,26)c) 4,92 - 0,48 = (R: 4,44)d) 12,3 - 1,74 = (R: 10,56)e) 3 - 0,889 = (R: 2,111)
f) 4,329 - 2 = (R: 2,329)g) 15,8 - 9,81 = (R: 5,99)h) 10,1 - 2,734 = (R: 7,366)
4) Calcule o valor das expressões
a) 5 - 1,3 + 2,7 = (R: 6,4)
b) 2,1 - 1,8 + 0,13 = (R: 0,43)
c) 17,3 + 0,47 - 8 = (R: 9,77)d) 3,25 - 1,03 - 1,18 = (R: 1,04)
e) 12,3 + 6,1 - 10,44 = (R: 7,96)
f) 7 - 5,63 + 1,625 = (R: 2,995)
5) Calcule o valor das expressões
a) (1 + 0,4) - 0,6 = (R: 0,8)
b) 0,75 + ( 0,5 - 0,2 ) = (R: 1,05)
c) ( 5 - 3,5 ) - 0,42 = (R: 1,08)
d) 45 - ( 14,2 - 8,3 ) = (R: 39,1)e) 12 + ( 15 - 10,456) = (R: 16,544)
f) 1,503 - ( 2,35 - 2,04) = (R: 1,193)
g) ( 3,8 - 1,6) - ( 6,2 - 5,02) = (R: 1,04)
h) ( 7 + 2,75 ) - ( 0,12 + 1,04) = (R: 8,59)
MULTIPLICAÇÃO DE NÚMEROS DECIMAIS
Multiplicamos os números decimais como se fossem números naturais. O números de casas decimais do produto é igual a soma do número de casas decimais dos fatores.
Exemplo
1) efetuar 2,45 x 3,2
2,46
x3,2
-----
7,872
2) efetuar 0,27 x 0,003
x0,27
0,003
-------
0,00081
EXERCÍCIOS
1) Efetue as multiplicações
a) 2 x 1,7= (R: 3,4)
b) 0,5 x 4 = (R: 2)c) 0,5 x 7 = (R: 3,5)d) 0,25 x 3 = (R: 0,75)
f) 6 x 3,21 = (R: 19,26)
2) Efetue as multiplicações
a) 5,7 x 1,4 = (R: 7,98)b) 0,42 x 0,3 = (R: 0,126)
c) 7,14 x 2,3 = (R: 16,422)
d) 14,5 x 0,5 = (R: 7,25)
e) 13,2 x 0,16 = (R 2,112)f) 7,04 x 5 = (R:35,2)
g) 21,8 x 0,32 = (R: 6,976)
h) 3,12 x 2,81 = (R: 8,7672)i) 2,14 x 0,008 = (R: 0,01712)j) 4,092 x 0,003 = (R: 0,012276)
3) Determine os seguintes produtos:
a) 0,5 x 0,5 x 0,5 = (R: 0,125)
b) 3 x 1,5 x 0,12 = (R: 6,75)
c) 5 x 0,24 x 0,1 = (R: 0,288)
d) 0,2 x 0,02 x 0,002 = (R: 0,000008)
e) 0,7 x 0,8 x 2,1 = (R: 1,176)
f) 3,2 x 0,1 x 1,7 = (R: 0,032)
4) calcule o valor das expressões
a) 3 x 2,5 - 1,5 = (R: 6)
b) 2 x 1,5 + 6 = (R: 9)
c) 3,5 x 4 - 0,8 = (R: 13,2)
d) 0,8 x 4 + 1,5 = (R: 4,7)
e) 2,9 x 5 - 8,01 = (R: 6,49)
f) 1,3 x 1,3 - 1,69 = (R: 0)
MULTIPLICAÇÃO POR POTENCIA DE 10
Para multiplicar por 10, 100, 1000, etc, basta deslocar a vírgula para a direita, uma, duas, três, etc casas decimais.
exemplos
a) 3,785 x 10 = 37,85
b) 3,785 x 100 = 378,5
c) 3,785 x 1000 = 3785
d) 0,0928 x 100 = 9,28
EXERCÍCIOS
1) Efetue as multiplicações:
a) 4,723 x 10 = (R: 47,23)
b) 8,296 x 100 = (R: 829,6)
c) 73,435 x 1000 = ( R: 73435)
d) 6,49 x 1000 = (R: 6490)e) 0,478 x 100 = (R: 478)
f) 3,08 x 1000 = (R: 3080)
g) 0,7 x 1000 = (R: 700)
h) 0,5 x 10 = (R: 5)
i) 3,7 x 1000 = (R: 3700)j) 0,046 x 10 = (R: 0,46)
DIVISÃO
Igualamos as casas decimais do dividendo e do divisor e dividimos como se fossem números naturais.
exemplos
1) efetuar 17,568 : 7,32
Igualando as casas decimais fica : 17568 : 7320 = 2,4
2) Efetuar 12,27 : 3
Igualando as casas decimais fica: 1227 : 300 = 4,09
exercícios
1) Efetuar as divisões:
a) 38,6 : 2 = (R: 19,3)
b) 7,6 : 1,9 = (R: 4)
c) 3,5 : 0,7 = (R: 5)d) 17,92 : 5,6 = (R: 3,2)
e) 155 : 0,25 = ( R: 620)f) 6,996 : 5,83 = (R: 1,2)g) 9,576 : 5,32 = (R: 1,8)
h) 2,280 : 0,05 = (R: 45,6)i) 1,24 : 0,004 = (R: 310)
j) 7,2624 : 2,136 = (R: 3,4)
2) Calcular o valor das expressões
a) 7,2 : 2,4 + 1,7 = (R: 4,7)b) 2,1 + 6,8 : 2 = (R: 5,5 )
c) 6,9 : 3 - 0,71 = (R: 1,59)
d) 8,36 : 2 - 1,03 = (R: 3,15)
e) 1,6 : 4 - 0,12 = (R: 0,28)
f) 8,7 - 1,5 : 0,3 = (R: 3,7)
DIVISÃO POR POTÊNCIA DE 10
Para dividir por 10, 100, 1000, etc, basta deslocar a vírgula para a esquerda, uma, duas três , etc casas decimais.
exemplos
a) 379,4 : 10 = 37,94
b) 379,4 : 100 = 3,794
c) 379,4 : 1000 = 0,3794
d) 42,5 ; 1000 = 0,0425
exercícios
1) Efetuar as divisões
a) 3,84 : 10 = (R: 0,384)b) 45,61 : 10 = (R: 4,561)c) 182,9 : 10 = ( R: 18,29)d) 274,5 : 100 = (R: 2,745)e) 84,34 : 100 = (R: 0,8434)f) 1634,2 : 100 =(R: 16,342)
g) 4781,9 : 1000 =( R: 4,7819)
h) 0,012 : 100 =(R: 0,0012)
i) 0,07 : 10 = (R: 0,007)
j) 584,36 : 1000 = (R: 0,58436)
2) efetue as divisões
a) 72 : 10²
b) 65 : 10³
c) 7,198 : 10²
d) 123,45 : 10⁴
POTENCIAÇÃO
A potenciação é uma multiplicação de fatores iguais
Exemplos:
1) (1,5)² = 1,5 x 1,5 = 2,25
2) (0,4)³ = 0,4 x 0,4 x 0,4 = 0,064
vamos lembrar que: são válidas as convenções para os expoentes um e zero.
Exemplos
1) (7,53)¹ = 7,53
2) ( 2,85)⁰ = 1
1) Calcule as potências
a) ( 0,7)²
b) (0,3) ²
c) (1,2) ²
d) (2,5) ²
e) (1,7) ²
f) (8,4) ²
g) (1,1)³
h) (0,1)³
i) (0,15) ²
j) (0,2)⁴
2) Calcule o valor das expressões
a) (1,2)³ + 1,3 =
b) 20 – (3,6) ² =
c) (0,2) ² + (0,8) ² =
d) (1,5) ² - (0,3) ² =
e) 1 – (0,9) ² =
f) 100 x (0,1)⁴ =
g) 4² : 0,5 – (1,5) ² =
h) ( 1 – 0,7) ² + ( 7 – 6)⁵
TRANSFORMAÇÃO DE FRAÇÕES EM NÚMEROS DECIMAIS
Para transformar uma fração em números decimais, basta dividir o numerador pelo denominador (obs o numerador é o números de cima da fração e o denominador o números debaixo)
Exemplos
transformar em números decimais as frações irredutíveis
1) 5/4 = 5 : 4 = 1,25 que será um, número decimal exato
2) 7/9 = 7 : 9 = 0,777... é uma dizima periódica simples
3) 5/6 = 5: 6 = 0,8333...... é uma dizima periódica composta
outros exemplos
a) 4,666... dízima periódica simples (período 6)
b) 2,1818....dízima periódica simples ( período 18)
c) 0,3535.... dízima periódica simples (período 35)
d) 0,8777.... dízima periódica composta (período 7 e parte não periódica 8)
e) 5,413333.... dízima periódica composta (período 3 e parte não periódica 41)
EXERCÍCIOS
1) Transforme em números decimais as frações:
a) 10/4 =
b) 4/5 =
c) 1/3 =
d) 5/3 =
e) 14/5 =
f) 1/6 =
g) 2/11 =
h) 43/99 =
i) 8/3 =
2) Transforme as frações decimais em números decimais :
a) 9/10 = (R: 0,9)
b) 57/10 = (R: 5,7)c) 815/10 = (R: 8,15)
d) 3/100 = (R: 0,03)e) 74/100 = (R: 0,74)
f) 2357/1000 = (R: 2,357)g) 7/1000 = (R: 0,007)
h) 15/10000 = (R: 0,0015)
i) 4782/10000 = (R: 0,4782)
Durante muito tempo, os números naturais eram os únicos números que o homem utilizava. Mas, com o passar do tempo, o homem foi encontrando situações mais difíceis para resolver. No antigo Egito, por exemplo, as terras próximas ao rio Nilo eram muito disputadas por isso os faraós tinham funcionários que mediam e demarcavam os terrenos.
Eles usavam cordas com nós separados sempre pela mesma distância. Em muitos casos, principalmente para efetuar medições, precisou criar outros números que não fossem apenas os números naturais. Surgiram assim, os números fracionários ou racionais.
Para representar os números fracionários foi criado um símbolo, que é a fração. Sendo a e b números racionais e b ≠ 0, indicamos a divisão de a por b com o símbolo a : b ou, ainda a/b
Chamamos o símbolo a/b de fração.
Assim, a fração 10/2 é igual a 10 : 2
Na fração a/b, a é o numerador e b é o denominador
Efetuando, por exemplo, a divisão de 10 por 2, obtemos o quociente 5.
Assim, 10/2 é um número natural, pois 10 é múltiplo de 2.
Mas efetuando a divisão de 3 por 4 não obtemos um número natural. Logo ¾ não é um número natural. A fração envolve a idéia de alguma coisa que foi dividida em partes iguais.
Agenor comeu ¾ de uma barra de chocolate. Que quantidade de chocolate Agenor comeu? Que parte da barra de chocolate sobrou?
Dividindo o chocolate em 4 partes, iguais temos;
Agenor comeu ¾ , portanto sobrou ¼
LEITURA DE UMA FRAÇÃO
Algumas frações recebem nomes especiais: as que têm denominadores 2,3,4,5,6,7,8,9
½ um meio
¼ um quarto
1/6 um sexto
1/8 um oitavo
2/5 dois quintos
9/8 nove oitavos
1/3 um terço
1/5 um quinto
1/7 um sétimo
1/9 um nono
4/9 quatro nonos
16/9 dezesseis nonos
as que tem denominadores 10, 100, 1000, etc.............
1/10 um décimo
1/100 um centésimo
1/1000 um milésimo
7/100 sete centésimos
as decimais que são lidas acompanhadas da palavra avos :
1/11 um onze avos
7/120 sete cento e vinte avos
4/13 quatro treze avos
1/300 um trezentos avos
5/19 cinco dezenove avos
6/220 seis duzentos e vinte avos
EXERCÍCIOS
1) indique as divisões em forma de fração:
a) 14 : 7 = (R: 14/7)
b) 18 : 8 = (R: 18/8)
c) 5 : 1 = (R: 5/1)d) 15 : 5 = ( R: 15/5)
e) 18 : 9 = (R: 18/9)
f) 64 : 8 = (R: 64/8)
2) Calcule o quociente das divisões
a) 12/3 = (R:4)
b) 42/21 = (R: 2)
c) 8/4 = (R: 2)d) 100/10 = (R: 10)
e) 56/7 = (R: 8)
f) 64/8 = (R: 8 )
3) Em uma fração, o numerador é 5 e o denominador é 6
a) Em quantas partes o todo foi dividido? (R: 6)b) Quantas partes do todo foram consideradas? (R: 5)
4) Escreva como se lêem as seguintes frações:
a) 5/8 (R: cinco oitavos)b) 9/10 (R: nove décimos)
c) 1/5 (R: um quinto)
d) 4/200 ( R: quatro duzentos avos)
e) 7/1000 (R: sete milésimos)
f) 6/32 (R: seis trinta e dois avos)
TIPOS DE FRAÇÕES
a) Fração própria : é aquela cujo o numerador é menor que o denominador.
Exemplos : 2/3, 4/7, 1/8
b) Fração imprópria: é a fração cujo numerador é maior ou igual ao denominador
Exemplo: 3/2, 5/5
c) Fração aparente: é a fração imprópria cujo o numerador é múltiplo do denominador
Exemplo: 6/2, 19/19, 24/12, 7/7
EXERCÍCIO
1) Classifique as frações em própria, imprópria ou aparente:
a) 8/9 (R: própria)
b) 10/10 (R: imprópria e aparente)
c) 26/13(R: imprópria e aparente)
d) 10/20 (R: própria)
e) 37/19 (R: imprópria)
f) 100/400 (R: própria)
FRAÇÕES EQUIVALENTES
Para encontrar frações equivalentes, multiplicamos o numerador e o denominador da fração ½ por um mesmo numero natural diferente de zero.
Assim: ½, 2/4, 4/8, 3/6, 5/10 são algumas frações equivalentes a 1/2
SIMPLIFICANDO FRAÇÕES
Cláudio dividiu a pizza em 8 partes iguais e comeu 4 partes. Que fração da pizza ele comeu?
Cláudio comeu 4/8 da pizza. Mas 4/8 é equivalente a 2/4. Assim podemos dizer que Cláudio comeu 2/4 da pizza.
A fração 2/4 foi obtida dividindo-se ambos os termos da fração 4/8 por 2 veja:
4/8 : 2/2 = 2/4
Dizemos que a fração 2/4 é uma fração simplificada de 4/8.
A fração 2/4 ainda pode ser simplificada, ou seja, podemos obter uma fração equivalente dividindo os dois termos da fração por 2 e vamos obter ½
OPERAÇÕES COM NÚMEROS RACIONAIS ABSOLUTOS (FRAÇÕES)
ADIÇÃO E SUBTRAÇÃO
1°) Como adicionarmos ou subtrairmos números fracionários escritos sob a forma de fração de denominadores iguais
Conclusão: Somamos os numeradores e conservamos o denominador comum.
Exemplo:
a) 5/7 – 2/7 = 3/7
b) 4/9+ + 2/9 = 6/9 = 2/3
c) 3/5 – 1/5 = 2/5
Exercícios
1) Efetue as adições
a) 3/6 + 2/6 = (R: 5/6)b) 13/7 + 1/7 = (R: 14/7)
c) 2/7+ 1/7 + 5/7 = (R: 8/7)d) 4/10 + 1/10 + 3/10 = (R: 8/10)
e) 5/6 + 1/6 = (R: 1)
f) 8/6 + 6/6 = (R: 14/6) = (R: 7/3)
g) 3/5 + 1/5 = (R: 4/5)
2) Efetue as subtrações:
a) 7/9 – 5/9 = (R: 2/9)
b) 9/5 -2/5 = (R: 7/5)
c) 2/3 – 1/3 = (R: 1/3)
d) 8/3 – 2/3 = (R: 6/3)
e) 5/6 – 1/6 = (R: 2/3)
f) 5/5 – 2/5 = (R: 3/5)
g) 5/7 – 2/7 = (R: 3/7)
3) Efetue as operações:
a) 5/4 + ¾ - ¼ = (R: 7/4)
b) 2/5 + 1/5 – 3/5 = (R: 0/5)
c) 8/7 – 3/7 + 1/7 = (R: 6/7)d) 7/3 – 4/3 – 1/3 = (R: 2/3)
e) 1/8 + 9/8 -3/8= (R: 7/8)
f) 7/3 – 2/3 + 1/3 = (R:6/3 ) = (R: 2)
g) 7/5 + 2/5 – 1/5 = (R: 8/5)
h) 5/7 – 2/7 – 1/7 = (R: 2/7)
2°) Como adicionarmos ou subtrairmos números fracionários escritos sob a forma de fração de denominadores diferentes
conclusão: Quando os denominadores são diferentes fazemos o m.m.c. dos denominadores .
exemplo:
a) 2/3 +1/2 = 4/6 + 3/6 = 7/6
3, 2 I 2
3, 1 I 3
1, 1 I ---2 . 3 = 6
b) 2/3 – ¼ = 8/12 – 3/12 = 5/12
3, 4 I 2
3, 2 I 2
3, 1 I 3
1, 1 I ----2 . 2. 3 = 12
exercícios
1) Efetue as adições:
a) 1/3 + 1/5 = (R: 8/15)
b) ¾ + ½ = (R: 5/4)
c) 2/4 + 2/3 = (R: 14/12)
d) 2/5 + 3/10 = (R: 7/10)
e) 5/3 + 1/6 = (R: 11/6)
f) ¼ + 2/3 + ½ = (R: 17/12)
g) ½ + 1/7 + 5/7 = (R: 19/14)
h) 3/7 + 5/2 + 1/14 = (R: 42/14)
i) 4/5 + 1/3 + 7/6 = (R: 69/30)
j) 1/3 + 5/6 + ¾ = (R: 23/12)
k) ½ + 1/3 + 1/6 = (R: 1)l) 10 + 1/8 + ¾ = (R: 85/8)
m) 1/3 + 3/5 = (R:14/15)
n) ¾ + 6/7 = (R: 45/28)
o) 5/7 + ½ = (R: 17/14)
p) ½ + 1/3 = (R: 5/6)
q) 3/14 + 3/7 = (R: 9/14)
r) 3/5 + ¾ + ½ = (R: 37/20)
s) 1/12 + 5/6 + ¾ = (R: 20/12)
t) 8 + 1/5 + 4/5 = (R: 45/5)
u)
2) efetue as subtrações
a) 5/4 – ½ = (R: 3/4)
b) 3/5 – 2/7 = (R: 11/35)
c) 8/10 – 1/5 = (R: 6/10)
d) 5/6 – 2/3 = (R: 1/6)
e) 4/3 – ½ = (R: 5/6)
f) 13/4 – 5/6 = (R: 29/12)
g) 7/8 – 1/6 = (R: 17/24)
h) 4/5 – 1/3 = (R: 7/15)
i) 3/5 – ¼ = (R: 7/20)
j) 10/11 – ½ = (R: 9/22)
l) 6/4 – 2/3 = (R: 10/12)
m) 5/8 – ½ = (R: 1/8)
n) 4/5 – ¼ = (R: 11/20)
o) ¾ - 5/8 = (R: 1/8)
p) 9/11 – ½ = (R: 7/22)
q) 7 – 2/3 = (R: 19/3)r) 4/2 - 2/3 = (R: 8/6)
s) 3/2 - 2/3 = (R: 5/6)
t) 1/2 - 1/3 = (R: 1/6)
u) 3/2 - 1/4 = (R: 5/4)
3) Efetue
a) 2 + 5/3 = (R: 11/3)
b) 7 + ½ = (R: 15/2)
c) 3/5 + 4 = (R: 23/5)
d) 6/7 + 1 = (R: 13/7)
e) 8 + 7/9 = (R: 79/9)
f) 5 – ¾ = (R: 17/4)
g) 2 – ½ = (R: 3/2)
h) 7/2 – 3 = (R: 1/2)
i) 11/2 – 3 = (R: 5/2)
j) 7/4 – 1 = (R: 3/4)
k) 1 – ¼ = (R: ¾ )
l) ½ - 1/3 = (R: 1/6)
m) ½ + ¼ = (R: ¾)
n) 1 + 1/5 = (R: 6/5)
o) 1 – 1/5 = (R: 4/5)
4) Calcule o valor das expressões:
a) 3/5 + ½ - 2/4 = (R: 12/20)
b) 2/3 + 5/6 – ¼ = (R: 15/12)c) 4/5 – ½ + ¾ = (R: 21/20)
d) 5/7 – 1/3 + ½ = (R: 37/42)
e) 1/3 + ½ - ¼ = (R: 7/12)
f) ¾ - ½ + 1/3 = (R: 7/12)
g) 5/6 – ½ + 2/3 = (R: 1)
h) 4/5 – ¾ + ½ = (R: 11/20)
i) ½ + 2/3 + 2/5 + 1/3 = (R: 57/30)
j) 6/5 – ¾ + ½ - 2/3 = (R: 17/60)l) 1/6 + 5/4 + 2/3 = (R: 25/12)
MULTIPLICAÇÃO
Vamos Calcular : 2/3 x 4/5 = 8/15
Conclusão : multiplicamos os numeradores entre si e os denominadores entre si
Exemplo:
a) 4/7 x 3/5 = 12/35
b) 5/6 x 3/7 = 15//42 = 5/14 simplificando
EXERCICIOS
1) Efetue as multiplicações
a) ½ x 8/8 = (R: 8/16)
b) 4/7 x 2/5 = (R: 8/35)
c) 5/3 x 2/7 = (R: 10/21)
d) 3/7 x 1/5 = (R: 3/35)
e) 1/8 x 1/9 = (R: 1/72)
f) 7/5 x 2/3 = (R: 14/15)
g) 3/5 x ½ = (R: 3/10)h) 7/8 x 3/2 = (R: 21/16)
i) 1/3 x 5/6 = (R: 5/18)
j) 2/5 x 8/7 = (R: 16/35)k) 7/6 x 7/6 = (R: 49/36)
l) 3/7 x 5/2 = (R: 15/14)
m) 3/10 x 5/9 = (R: 15/90)
n) 2/3 x ¼ x 5/2 = (R: 10/24)
o) 7 x ½ x 1/3 = (R: 7/6)
p)
2) Efetue as multiplicações
a) 4/3 x ½ x 2/5 = (R: 8/30)
b) 1/5 x ¾ x 5/3 = (R: 15/60)
c) ½ x 3/7 x 1/5 = (R: 3/70)d) 3/2 x 5/8 x ¼ = (R: 15/64)
e) 5/4 x 1/3 x 4/7 = (R: 20/84)
3) Efetue as multiplicações
a) 2 x 5/3 = (R: 10/3)
b) 3 x 2/5 = (R: 6/5)
c) 1/8 x 5 = (R: 5/8)d) 6/7 x 3 = (R: 18/7)e) 2 x 2/3 x 1/7 = (R: 4/21)
f) 2/5 x 3 x 4/8 = (R: 24/40)
g) 5 x 2/3 x 7 = (R: 70/3)
h) 7/5 x 2 x 4 = (R: 56/5)
i) 8 x 2/3 = (R: 16/3)
j) 5/9 x 0/6 = (R: 0/54)
k) 1/7 x 40 = (R: 40/7)l) ½ x 1/3 x ¼ x 1/5 = (R: 1/120)m) 1 x 2/3 x 4/3 x 1/10 = (R: 8/90)
DIVISÃO
Vamos calcular ½ : 1/6
Para dividir uma fração por outra, basta multiplicar a primeira fração pela inversa da segunda
Assim: ½ : 1/6 = ½ x 6/1 = 6/2 = 3
Exemplos:
a) 2/3 : 5/2 = 2/3 x 2/5 = 4/15
b) 7/9 : 1/5 = 7/9 x 5/1 = 35//9
c) 3/7 : 4 = 3/7 x ¼ = 3/28
Exercícios
1) Efetue as divisões
a) ¾ : 2/5 = (R: 15/8)
b) 5/7 : 2/3 = (R: 15/14)
c) 4/5 : 3/7 = (R: 28/15)
d) 2/9 : 7/8 = (R: 16/63)
e) 1/6 : 5/3 = (R: 3/30) ou (3/10)
f) 7/8 : ¾ = (R: 28/24) ou (7/6)g) 8/7 : 9/3 = (R: 24/63)
h) 4/5 : 2/5 = (R: 20/10) ou (2/1) ou ( 2)i) 5/8 : ¾ = (R: 20/24) ou (5/6)
j) 2/9 : 4/7 = (R: 14/36) ou (7/18)
2) Efetue as divisões :
a) 5 : 2/3 = (R: 15/2)
b) 4 : 1/7 = (R: 28/1) ou (28)
c) 8/9 : 5 = (R: 8/45)
d) 3/7 : 3 = (R: 3/21)
e) 7/3 : 4/7 = (R: 49/12)
f) 2/3 : ½ = (R: 4/3)
g) 4/5 : 2/3 = (R: 12/10)
h) 2/7 : 5/3 = (R: 6/35)
i) 3/7 : 2 = (R: 3/14)
j) 3/2 : 5/7 = (R: 21/10)
k) 3/8 : 4/7 = (R: 21/32)
POTENCIAÇÃO
Vamos calcular a potência (2/5)³= 2/5 x 2/5 x 2/5 = 8/125
Conclusão: para elevar uma fração a um expoente, elevam-se o numerador e o denominador da fração desse expoente.
Exemplo
a) (5/7)² = 5²/ 7² = 25/49
1) Toda fração de expoente 1 dá como resultado a própria fração
Exemplo: (3/8)¹ = 3/8
2) Toda a fração elevada ao expoente zero dá como resultado o número 1
Exemplo : (3/4)⁰ = 1
Exercícios
1) Calcule as potências
a) (2/3)² = (R: 4/9)
b) (4/7)² = (R: 16/49)
c) (7/5)² = (R: 49/25)
d) (1/3)² = (R: 1/9)
e) (5/3)² = (R: 25/9)
f) (7/30)⁰ = ( R: 1)
g) (9/5)¹ = (R: 9/5)
h) (2/3)³ = (R: 8/27)
i) (1/5)³ = (R: 1/125)
j) (1/2)² = (R: 1/4)
k) (2/3)⁴= (R: 16/81)
l) (2/5)¹ = (R: 2/5)
m) (3/11)² = (R: 9/121)
n) (9/4)⁰ = (R: 1)o) (12/13)² = (R: 144/169)
p) (1/2)⁵ = (R: 1/32)q) (3/7)³ = ( R: 27/343)
RAIZ QUADRADA DE NÚMEROS RACIONAIS (FRAÇÃO)
Sabemos que :
√25 = 5
√49 = 7
√25/49 = 5/7
Conclusão:
Para extrair a raiz quadrada de um número fracionário, extraem-se a raiz quadrada do numerador e a raiz quadrada do denominador.
Exemplos
a) √4/9 = 2/3
b) √1/36 = 1/6
Exercícios
1) Calcule a raiz quadrada
a) √9/16 = (R: 3/4)
b) √1/25 = (R:1/5)
c) √9/25 = (R: 3/5)
d) √16/49 = (R: 4/7)
e) √64/25 = (R: 8/5)
f) √1/9 = (R: 1/3)
g) √25/81 = (R: 5/9)
h) √49/36 = (R: 7/6)
i) √1/100 = (R: 1/10)
EXPRESSÕES COM NÚMEROS RACIONAIS
As expressões com números racionais devem ser resolvidas obedecendo à seguinte ordem de operações:
1°) Potenciação e Radiciação
2°) Multiplicação e Divisão
3°) Adição e subtração
Essas operações são realizadas eliminando :
1°) Parênteses
2°) Colchetes
3°) Chaves
exemplos:
1) 1/5 + 4/5 x 1/3 =
1/5 + 4/15 =
3/15 + 4/15 =
7/15
2) (3/5)² + 2/5 x ½ =
9/25 + 2/10 =
18/50 + 10/50 =
= 28/50 = 14/25
3) ( 4 + ½ ) – 1/5 : 2/3 =
( 8/2 + ½ ) – 1/5 : 2/3 =
9/2 – 1/5 : 2/3 =
9/2 – 1/5 x 3/2 =
9/2 – 3/10 =
45/10 – 3/10 =
= 42/10 = 21/5
Exercícios
1) Calcule o valor das expressões:
a) 5/8 + ½ -2/3 = (R: 11/24)
b) 5 + 1/3 -1/10 = (R: 157/30)
c) 7/8 – ½ - ¼ = (R: 1/8)
d) 2/3 + 3 + 1/10 = (R: 113/30)
e) ½ + 1/6 x 2/3 = (R: 11/18)
f) 3/10 + 4/5 : ½ = (R: 19/10)
g) 2/3 x ¾ - 1/6 = (R: 4/12 ou 1/3)
h) 7 – ¼ + 1/7 = (R: 193/28)
i) 3 x ½ - 4/5 = (R: 7/10)
j) 7/4 – ¼ x 3/2 = ( R: 11/8)k) ½ + 3/2 x ½ = ( R: 5/4)
l) 1/10 + 2/3 x ½ = (R: 13/30)
2) Calcule o valor da expressão:
a) 7 x ½ + (4/5)² = (R: 207/50)
b) (1/3)² + 2/5 x ½ = (R: 28/90 ) ou (14/45)
c) (1/2)² : ¾ + 5/3 = ( R: 24/12) ou (2)d) (1/3)² x 5/2 + ½ = ( R: 14/18) ou (7/9)
e) 2/5 x ½ + ( 3/5)² = ( R: 28/50) ou (14/25)f) (2/3)²+ 4 + 1/3 -1/2 = ( R: 77/18)
3) Calcule o valor da expressão:
a) 5/6 – ( 1/3 + 1/5 ) = ( R: 9/30) ou (3/10)
b) 2/5 x ( ¾ + 5/8) = ( R: 22/40) ou (11/20)c) ½ : ( 2/3 + ¾ ) = ( R: 12/34) ou ( 6/17)
d) ( 1/3 + ½ ) : 5/6 = (R: 30/30) ou (1)
e) ½ . ( 2/3 + ¾ ) = ( R: 17/24)f) ( 5/7 x 2/3 ) : 1/6 = (R: 60/21)
g) (3/2 - 2/5 ) + ( 5/4 - 2/3) = (R: 101/60)
h) 1 + (1/2 - 1/5) - (7/4 - 5/4) = (R: 16/20)i) ( 7/8 - 5/6) + ( 8/9 - 7/9) = (R: 11/72)
4) Calcule o valor das expressões
a) ( ¾ x ½ + 2/5 ) + ¼ = (R: 41/40)b) ( 2/3 x ¼ ) + ( 1/3 x ½ ) = (R: 4/12)
c) ( 5- ½ ) : ( 2 – 1/3) = ( R: 27/10)d) ( 3 x 5/2 ) : ( 1/5 + 1/3 ) = (R: 225/16)
e) ( 3 x ¾ ) + ( 3 x ¼ ) = ( R: 12/4)
f) ( 3 + ½ ) x 4/5 – 3/10 = (R: 25/10)
5) Calcule o valor das expressões
a) ½ : 1/3 + ¾ x 5/9 = ( R: 69/36)
b) 3/8 x ( ½ x 4/3 + 4/3 ) = (R: 36/48)
c) ( 1/3 + ¼ ) : 5/2 + 2/3 = (R: 54/60)
d) ( ¾ + ¼ - ½ ) : 3/2 = (R: 8/11)
d) ( 1 + 1/3 )² x 9/4 + 6 = (R: 360/36)
e) 1 + (3/2)² + ( 1 + ¼ ) = (R: 18/4)
6) calcule o valor das expressões
PROBLEMAS COM NÚMEROS RACIONAIS
Os problemas com números racionais absolutos são geralmente resolvidos da seguinte forma :
1°) Encontrando o valor de uma unidade fracionária
2°) obtendo o valor correspondente da fração solicitada
exemplo
Eu tenho 60 fichas, meu irmão tem ¾ dessa quantidade. Quantas fichas tem o meu irmão ?
60 x ¾ = 180/4 = 45
R: O meu irmão tem 45 fichas
EXERCICIOS
1) Determine 2/3 de R$ 1200,00 (R: 800)
2) Numa caixa existem 80 bombons. Calcule 2/5 desses bombons. (R: 32)
3) O comprimento de uma peça de tecido é de 42 metros. Quanto medem 3/7 dessa peça ? (R: 18 m)
4) Um automóvel percorreu 3/5 de uma estrada de 600 km. Quantos quilômetros percorreu? (R: 360 km)
5) Numa viagem de 72 km, já foram percorridos ¾ . Quantos quilômetros já foram percorridos? (R : 54 km)
6) Um livro tem 240 páginas., Você estudou 5/6 do livro. Quantas paginas você estudou? (R: 200)
7) Os 2/5 de um número correspondem a 80. Qual é esse número? (R: 200)
8) Os ¾ do que possuo equivalem a R$ 900,00. Quanto possuo? (R: 1200)
9) Um time de futebol marcou 35 gols, correspondendo a 7/15 do total de gols do campeonato. Quantos gols foram marcados no campeonato? (R: 75)
10) Para encher 1/5 de um reservatório são necessários 120 litros de água. Quanto é a capacidade desse reservatório? (R: 600 litros)
11) Se 2/9 de uma estrada corresponde a 60 km, quantos quilômetros tem essa estrada?
(R: 270 km)
12) Para revestir ¾ de uma parede foram empregados 150 azulejos. Quantos azulejos são necessários para revestir toda a parede? (R: 200)
13) De um total de 240 pessoas,1/8 não gosta de futebol. Quantas pessoas gostam de futebol?
(R: 210)
14) Eu fiz uma viagem de 700 km. Os 3/7 do percurso foram feitos de automóvel e o restante de ônibus. Que distancia eu percorri de ônibus? (R: 400 km)
15) Numa prova de 40 questões um aluno errou ¼ da prova. Quantas questões ele acertou?
(R: 30 )
16) Numa classe de 45 alunos, 3/5 são meninas. Quantos meninos há nessa classe? (R: 18)
17) Um brinquedo custou R$ 152,10,. Paguei 1/6 do valor desse objeto. Quanto estou devendo?
(R: 126,75)
NÚMEROS DECIMAIS
FRAÇÃO DECIMAL
Chama-se fração decimal toda fração cujo denominador é 10 ou potência de 10 ex 10, 100, 100...
como:
a) 7/10
b) 3/100
c) 27/1000
NÚMEROS DECIMAIS
a) 7/10 = 0,7
b) 3/100 = 0,03
c) 27/1000 = 0,027
nos números decimais , a virgula separa a parte inteira da parte decimal
LEITURA DO NÚMERO DECIMAL
Para ler um, número decimal, procedemos do seguinte modo:
1°) Lêem -se os inteiros
2°) Lê-se a parte decimal, seguida da palavra:
décimos - se houver uma casa decimal
centésimos - se houver duas casas decimais
milésimos - se houver três casas decimais
exemplos:
a) 5,3 - lê-se cinco inteiros e três décimos
b) 1,34 - lê-se um inteiro e trinta e quatro centésimos
c) 12,007 - lê-se doze inteiros e sete milésimos
quando a parte inteira for zero, lê-se apenas a parte decimal
a) 0,4 - lê-se quatro décimos
b) 0,38 - lê-se trinta e oito centésimos
TRANSFORMAÇÃO DE FRAÇÃO DECIMAL EM NÚMERO DECIMAL
Para transformar uma fração decimal em número decimal, escrevemos o numerador e separamos, à direita da virgula, tantas casas quanto são os zeros do denominador
exemplos:
a) 42/10 = 4,2
b) 135/100 = 1,35
c) 135/1000 = 0,135
Quando a quantidade de algarismos do númerador não for suficiente para colocar a vírgula, acrescentamos zeros à esquerda do número.
exemplo:
a) 29/1000 = 0,029
b) 7/1000 = 0,007
EXERCÍCIOS ,
1) transforme as frações em números decimais
a) 3/10 = (R: 0,3)
b) 45/10 = (R: 4,5)
c) 517/10 = (R:51,7)
d) 2138/10 = (R: 213,8)
e) 57/100 = (R: 0,57)f) 348/100 = (R: 0,348)
g) 1634/100 = (R: 1,634)
h) 328/ 1000 = (R: 0,328)
i) 5114 / 1000 = (R: 5,114)
j) 2856/1000 = (R: 2,856)l) 4761 / 10000 = (R: 0,4761)
m) 15238 /10000 = (R: 1,5238)
2) transforme as frações em números decimais
a) 9 / 100 = (R: 0,09)
b) 3 / 1000 = (R: 0,003)c) 65 /1000 = (R: 0,065)d) 47 /1000 = (R: 0,047)e) 9 / 10000 = (R: 0,0009)f) 14 / 10000 = (R: 0,0014)
TRANSFORMAÇÃO DE NÚMERO DECIMAL EM FRAÇÃO
Procedimentos:
1) O numerador é um número decimal sem a virgula
2) O denominador é o número 1 acompanhado de tantos zeros quantos forem os algarismos do número decimal depois da vírgula.
exemplos:
a) 0,7 = 7/10
b) 8,34 / 834 /100
0,005 = 5/ 1000
EXERCÍCIOS
1) Transforme os números decimais em frações
a) 0,4 = (R: 4/10)b) 7,3 = (R: 73/10)
c) 4,29 = (R: 429/100)
d) 0,674 = (R: 674/1000)
e) 8,436 = (R: 8436/1000)f) 69,37 = (R: 6937/100)
g) 15,3 = (R: 153/10)
h) 0,08 = (R: 8/100)
i) 0,013 = (R: 13/1000)j) 34,09 = (R: 3409/100)l) 7,016 = (R: 7016/1000)m) 138,11 = (R: 13811/100)
OPERAÇÕES COM NÚMEROS DECIMAIS
ADIÇÃO E SUBTRAÇÃO
Colocamos vírgula debaixo de vírgula e operamos como se fossem números naturais>
exemplo
1) Efetuar 2,64 + 5,19
2,64
5,19 +
----
7,83
2) Efetuar 8,42 - 5,61
8,42
5,61 -
----
2,81
Se o número de casas depois da virgula for diferente, igualamos com zeros à direita
3) Efetuar 2,7 + 5 + 0,42
2,70
5,00 +
0,42
----
8,12
4) efetuar 4,2 - 2,53
4,20
2,53 -
------
1,67
EXERCÍCIOS
1) Calcule
a) 1 + 0,75 = (R: 1,75)b) 0,8 + 0,5 = (R: 1,3)c) 0,5 + 0,5 = (R: 1,0)d) 2,5 + 0,5 + 0,7 = (R: 3,7)e) 0,5 + 0,5 + 1,9 + 3,4 = (R:6,3)
f) 5 + 0,6 + 1,2 + 15,7 = (R: 22,5)
2) Efetue as adições
a) 3,5 + 0,12 = (R: 3,62)
b) 9,1 + 0,07 = (R: 9,17)
c) 4,7 + 12,01 = (R: 16,71)
d) 2,746 + 0,92 = (R: 3,666)
e) 6 + 0,013 = (R: 6,013)f) 4 + 0,07 + 9,1 = (R: 13,17)g) 16.,4 + 1,03 + 0,72 = (R: 18,15)h) 5,3 + 8,2 + 0,048 = (R: 13,548)
i) 0,45 + 4,125 + 0,001 = (R: 4,576)
3) Efetue as subtrações
a) 8,2 - 1,7 = (R: 6,5)b) 5 - 0,74 = (R: 4,26)c) 4,92 - 0,48 = (R: 4,44)d) 12,3 - 1,74 = (R: 10,56)e) 3 - 0,889 = (R: 2,111)
f) 4,329 - 2 = (R: 2,329)g) 15,8 - 9,81 = (R: 5,99)h) 10,1 - 2,734 = (R: 7,366)
4) Calcule o valor das expressões
a) 5 - 1,3 + 2,7 = (R: 6,4)
b) 2,1 - 1,8 + 0,13 = (R: 0,43)
c) 17,3 + 0,47 - 8 = (R: 9,77)d) 3,25 - 1,03 - 1,18 = (R: 1,04)
e) 12,3 + 6,1 - 10,44 = (R: 7,96)
f) 7 - 5,63 + 1,625 = (R: 2,995)
5) Calcule o valor das expressões
a) (1 + 0,4) - 0,6 = (R: 0,8)
b) 0,75 + ( 0,5 - 0,2 ) = (R: 1,05)
c) ( 5 - 3,5 ) - 0,42 = (R: 1,08)
d) 45 - ( 14,2 - 8,3 ) = (R: 39,1)e) 12 + ( 15 - 10,456) = (R: 16,544)
f) 1,503 - ( 2,35 - 2,04) = (R: 1,193)
g) ( 3,8 - 1,6) - ( 6,2 - 5,02) = (R: 1,04)
h) ( 7 + 2,75 ) - ( 0,12 + 1,04) = (R: 8,59)
MULTIPLICAÇÃO DE NÚMEROS DECIMAIS
Multiplicamos os números decimais como se fossem números naturais. O números de casas decimais do produto é igual a soma do número de casas decimais dos fatores.
Exemplo
1) efetuar 2,45 x 3,2
2,46
x3,2
-----
7,872
2) efetuar 0,27 x 0,003
x0,27
0,003
-------
0,00081
EXERCÍCIOS
1) Efetue as multiplicações
a) 2 x 1,7= (R: 3,4)
b) 0,5 x 4 = (R: 2)c) 0,5 x 7 = (R: 3,5)d) 0,25 x 3 = (R: 0,75)
f) 6 x 3,21 = (R: 19,26)
2) Efetue as multiplicações
a) 5,7 x 1,4 = (R: 7,98)b) 0,42 x 0,3 = (R: 0,126)
c) 7,14 x 2,3 = (R: 16,422)
d) 14,5 x 0,5 = (R: 7,25)
e) 13,2 x 0,16 = (R 2,112)f) 7,04 x 5 = (R:35,2)
g) 21,8 x 0,32 = (R: 6,976)
h) 3,12 x 2,81 = (R: 8,7672)i) 2,14 x 0,008 = (R: 0,01712)j) 4,092 x 0,003 = (R: 0,012276)
3) Determine os seguintes produtos:
a) 0,5 x 0,5 x 0,5 = (R: 0,125)
b) 3 x 1,5 x 0,12 = (R: 6,75)
c) 5 x 0,24 x 0,1 = (R: 0,288)
d) 0,2 x 0,02 x 0,002 = (R: 0,000008)
e) 0,7 x 0,8 x 2,1 = (R: 1,176)
f) 3,2 x 0,1 x 1,7 = (R: 0,032)
4) calcule o valor das expressões
a) 3 x 2,5 - 1,5 = (R: 6)
b) 2 x 1,5 + 6 = (R: 9)
c) 3,5 x 4 - 0,8 = (R: 13,2)
d) 0,8 x 4 + 1,5 = (R: 4,7)
e) 2,9 x 5 - 8,01 = (R: 6,49)
f) 1,3 x 1,3 - 1,69 = (R: 0)
MULTIPLICAÇÃO POR POTENCIA DE 10
Para multiplicar por 10, 100, 1000, etc, basta deslocar a vírgula para a direita, uma, duas, três, etc casas decimais.
exemplos
a) 3,785 x 10 = 37,85
b) 3,785 x 100 = 378,5
c) 3,785 x 1000 = 3785
d) 0,0928 x 100 = 9,28
EXERCÍCIOS
1) Efetue as multiplicações:
a) 4,723 x 10 = (R: 47,23)
b) 8,296 x 100 = (R: 829,6)
c) 73,435 x 1000 = ( R: 73435)
d) 6,49 x 1000 = (R: 6490)e) 0,478 x 100 = (R: 478)
f) 3,08 x 1000 = (R: 3080)
g) 0,7 x 1000 = (R: 700)
h) 0,5 x 10 = (R: 5)
i) 3,7 x 1000 = (R: 3700)j) 0,046 x 10 = (R: 0,46)
DIVISÃO
Igualamos as casas decimais do dividendo e do divisor e dividimos como se fossem números naturais.
exemplos
1) efetuar 17,568 : 7,32
Igualando as casas decimais fica : 17568 : 7320 = 2,4
2) Efetuar 12,27 : 3
Igualando as casas decimais fica: 1227 : 300 = 4,09
exercícios
1) Efetuar as divisões:
a) 38,6 : 2 = (R: 19,3)
b) 7,6 : 1,9 = (R: 4)
c) 3,5 : 0,7 = (R: 5)d) 17,92 : 5,6 = (R: 3,2)
e) 155 : 0,25 = ( R: 620)f) 6,996 : 5,83 = (R: 1,2)g) 9,576 : 5,32 = (R: 1,8)
h) 2,280 : 0,05 = (R: 45,6)i) 1,24 : 0,004 = (R: 310)
j) 7,2624 : 2,136 = (R: 3,4)
2) Calcular o valor das expressões
a) 7,2 : 2,4 + 1,7 = (R: 4,7)b) 2,1 + 6,8 : 2 = (R: 5,5 )
c) 6,9 : 3 - 0,71 = (R: 1,59)
d) 8,36 : 2 - 1,03 = (R: 3,15)
e) 1,6 : 4 - 0,12 = (R: 0,28)
f) 8,7 - 1,5 : 0,3 = (R: 3,7)
DIVISÃO POR POTÊNCIA DE 10
Para dividir por 10, 100, 1000, etc, basta deslocar a vírgula para a esquerda, uma, duas três , etc casas decimais.
exemplos
a) 379,4 : 10 = 37,94
b) 379,4 : 100 = 3,794
c) 379,4 : 1000 = 0,3794
d) 42,5 ; 1000 = 0,0425
exercícios
1) Efetuar as divisões
a) 3,84 : 10 = (R: 0,384)b) 45,61 : 10 = (R: 4,561)c) 182,9 : 10 = ( R: 18,29)d) 274,5 : 100 = (R: 2,745)e) 84,34 : 100 = (R: 0,8434)f) 1634,2 : 100 =(R: 16,342)
g) 4781,9 : 1000 =( R: 4,7819)
h) 0,012 : 100 =(R: 0,0012)
i) 0,07 : 10 = (R: 0,007)
j) 584,36 : 1000 = (R: 0,58436)
2) efetue as divisões
a) 72 : 10²
b) 65 : 10³
c) 7,198 : 10²
d) 123,45 : 10⁴
POTENCIAÇÃO
A potenciação é uma multiplicação de fatores iguais
Exemplos:
1) (1,5)² = 1,5 x 1,5 = 2,25
2) (0,4)³ = 0,4 x 0,4 x 0,4 = 0,064
vamos lembrar que: são válidas as convenções para os expoentes um e zero.
Exemplos
1) (7,53)¹ = 7,53
2) ( 2,85)⁰ = 1
1) Calcule as potências
a) ( 0,7)²
b) (0,3) ²
c) (1,2) ²
d) (2,5) ²
e) (1,7) ²
f) (8,4) ²
g) (1,1)³
h) (0,1)³
i) (0,15) ²
j) (0,2)⁴
2) Calcule o valor das expressões
a) (1,2)³ + 1,3 =
b) 20 – (3,6) ² =
c) (0,2) ² + (0,8) ² =
d) (1,5) ² - (0,3) ² =
e) 1 – (0,9) ² =
f) 100 x (0,1)⁴ =
g) 4² : 0,5 – (1,5) ² =
h) ( 1 – 0,7) ² + ( 7 – 6)⁵
TRANSFORMAÇÃO DE FRAÇÕES EM NÚMEROS DECIMAIS
Para transformar uma fração em números decimais, basta dividir o numerador pelo denominador (obs o numerador é o números de cima da fração e o denominador o números debaixo)
Exemplos
transformar em números decimais as frações irredutíveis
1) 5/4 = 5 : 4 = 1,25 que será um, número decimal exato
2) 7/9 = 7 : 9 = 0,777... é uma dizima periódica simples
3) 5/6 = 5: 6 = 0,8333...... é uma dizima periódica composta
outros exemplos
a) 4,666... dízima periódica simples (período 6)
b) 2,1818....dízima periódica simples ( período 18)
c) 0,3535.... dízima periódica simples (período 35)
d) 0,8777.... dízima periódica composta (período 7 e parte não periódica 8)
e) 5,413333.... dízima periódica composta (período 3 e parte não periódica 41)
EXERCÍCIOS
1) Transforme em números decimais as frações:
a) 10/4 =
b) 4/5 =
c) 1/3 =
d) 5/3 =
e) 14/5 =
f) 1/6 =
g) 2/11 =
h) 43/99 =
i) 8/3 =
2) Transforme as frações decimais em números decimais :
a) 9/10 = (R: 0,9)
b) 57/10 = (R: 5,7)c) 815/10 = (R: 8,15)
d) 3/100 = (R: 0,03)e) 74/100 = (R: 0,74)
f) 2357/1000 = (R: 2,357)g) 7/1000 = (R: 0,007)
h) 15/10000 = (R: 0,0015)
i) 4782/10000 = (R: 0,4782)
Cubo da soma e cubo da diferença
Professor de Matemática no Colégio Estadual Dinah Gonçalves
E Biologia na rede privada de Salvador-Bahia
Professor Antonio Carlos carneiro Barroso
email accbarroso@hotmail.com
http://accbarrosogestar.blogspot.com.br
Cubo da soma e cubo da diferença
Por Marcelo Rigonatto
Calculo de produtos notáveis
Cubo da soma
Sejam a e b números reais diferentes de zero. Temos que:
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + 2a2b +ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
Observe que utilizamos o quadrado da soma, que é outro produto notável, para obter o cubo da soma. De uma forma geral, o cubo da soma pode ser obtido da seguinte maneira:
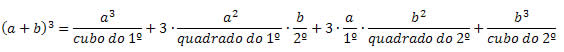
Cubo da diferença
O cubo da diferença é feito de maneira análoga ao cubo da soma. Observe:
(a – b)3 = (a – b)2(a – b) = (a2 – 2ab + b2)(a – b) = a3 – 3a2b + 3ab2 – b3
De uma forma geral, temos:
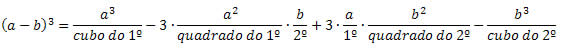
Vejamos alguns exemplos para melhor esclarecimento.
Exemplo 1. Desenvolva os seguintes produtos notáveis.
Solução:
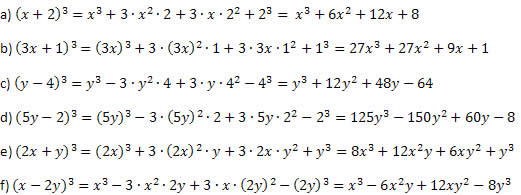
Procedendo como foi explicado antes do exemplo e tendo o cuidado ao realizar as potências e a multiplicações, não há como errar. O procedimento é sempre o mesmo para o cubo da soma e para o cubo da diferença, diferindo somente o sinal do segundo membro e do último.
Exemplo 2. Simplifique a expressão abaixo.
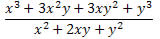
Solução: Observe que no numerador e no denominador da fração aparecem dois produtos notáveis. No numerador há um cubo da soma de dois termos que foi desenvolvido e no denominador, um quadrado da soma de dois termos. Assim, podemos reescrevê-los da seguinte forma:
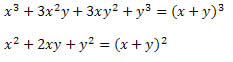
Logo, a expressão pode ser escrita como:
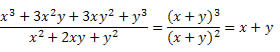
Para chegar ao resultado utilizamos a propriedade da divisão de potências de bases iguais (conserva a base e subtrai os expoentes).
Exemplo 3. Desenvolva o seguinte produto notável
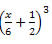
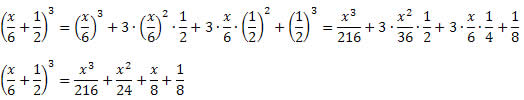
Função composta
www.youtube.com/accbarroso1
Seja f (x) = 2x, g (x) = 3x – 1 e h (x) = x². Obter f О g О h(2).
Note que, Obter f О g О h(2) = f [ g О h (2)] (1)
* Resolvemos primeiro o que está em colchetes.
[ g О h (2)] = g[j(2)] = g (4) = 11
* Agora voltaremos à expressão (1)
f [ g О h(2)] = f (11) = 22
Dessa forma, f О g О h(2) = 22
Transformações no Gráfico de y = f (x)
Pontos Simétricos em Relação ao eixo Ox
Y = f (x) e y = -f (x)
O gráfico de y = f (x) é a parábola representada na figura abaixo:
Para construir o gráfico de y = -f (x), basta perceber que, enquanto os pontos do gráfico de y = f (x) são da forma (x; f (x)), os pontos do gráfico y = -f (x) são da forma (x; -f(x)). Ou seja, os pontos do gráfico são simétricos aos pontos do primeiro, em relação ao eixo Ox.
Desse modo, o gráfico da função y = -f (x) é a curva simétrica do gráfico de y = f(x) em relação ao eixo das abscissas.
Y = f(x) e y = │f (x)│
A definição de módulo de f(x) é:
│f (x)│ = f(x), se f(x) ≥ 0
-f(x), se f(x) < 0 Dessa forma, para obter o gráfico de y = │f (x)│, basta rebater simetricamente em relação ao eixo das abscissas, apenas a parte do gráfico de y = f(x) que se encontra abaixo do eixo Ox, pois nessa região f(x) < 0. y = f (x) ± λ O gráfico de uma função da forma y = f(x) ± λ pode ser construído a partir do gráfico de y = f(x), deslocando o último na direção vertical. Tal deslocamento é chamado translação do gráfico de y = f(x). Supondo λ > 0, há duas considerações a fazer:
O gráfico de y = f(x) + λ é uma translação vertical do gráfico de y = f(x) para cima
O gráfico de y = f(x) – λ é uma translação vertical do gráfico de y = f(x) para baixo
y = f(x ± λ)
O gráfico de y = f(x - λ) é uma translação horizontal do gráfico de y = f(x) para a direita.
Seja f (x) = 2x, g (x) = 3x – 1 e h (x) = x². Obter f О g О h(2).
Note que, Obter f О g О h(2) = f [ g О h (2)] (1)
* Resolvemos primeiro o que está em colchetes.
[ g О h (2)] = g[j(2)] = g (4) = 11
* Agora voltaremos à expressão (1)
f [ g О h(2)] = f (11) = 22
Dessa forma, f О g О h(2) = 22
Transformações no Gráfico de y = f (x)
Pontos Simétricos em Relação ao eixo Ox
Y = f (x) e y = -f (x)
O gráfico de y = f (x) é a parábola representada na figura abaixo:
Para construir o gráfico de y = -f (x), basta perceber que, enquanto os pontos do gráfico de y = f (x) são da forma (x; f (x)), os pontos do gráfico y = -f (x) são da forma (x; -f(x)). Ou seja, os pontos do gráfico são simétricos aos pontos do primeiro, em relação ao eixo Ox.
Desse modo, o gráfico da função y = -f (x) é a curva simétrica do gráfico de y = f(x) em relação ao eixo das abscissas.
Y = f(x) e y = │f (x)│
A definição de módulo de f(x) é:
│f (x)│ = f(x), se f(x) ≥ 0
-f(x), se f(x) < 0 Dessa forma, para obter o gráfico de y = │f (x)│, basta rebater simetricamente em relação ao eixo das abscissas, apenas a parte do gráfico de y = f(x) que se encontra abaixo do eixo Ox, pois nessa região f(x) < 0. y = f (x) ± λ O gráfico de uma função da forma y = f(x) ± λ pode ser construído a partir do gráfico de y = f(x), deslocando o último na direção vertical. Tal deslocamento é chamado translação do gráfico de y = f(x). Supondo λ > 0, há duas considerações a fazer:
O gráfico de y = f(x) + λ é uma translação vertical do gráfico de y = f(x) para cima
O gráfico de y = f(x) – λ é uma translação vertical do gráfico de y = f(x) para baixo
y = f(x ± λ)
O gráfico de y = f(x - λ) é uma translação horizontal do gráfico de y = f(x) para a direita.
Geogebra
Um programa capaz de realizar cálculos de álgebra / geometria e que possibilita a Construção de gráficos. "
Ganhador diversos prêmios na Europa, o GeoGebra é UM programa de matemática dinâmica, feito com o intuito de ser utilizado em sala de aula, o Qual Junta aritmética, álgebra, geometria e cálculo. O GeoGebra possibilita o desenho de pontos, vetores, segmentos, linho e funções, e ainda, a alteração Dinâmica deles, assim que terminados.
Com o GeoGebra tambem é possivel inserir equações e coordenadas diretamente nos gráficos. Além disse, ele consegue lidar com variaveis de números, vetores e pontos, encontrar derivadas, integrais de funções e, até mesmo, oferece diversos comandos para a resolução de contas.
Instalação e uso
Apesar de possuir UMA instalação cheia de Passos, o GeoGebra é fácil de usar (até porque ele está em português). Basicamente, para usa-lo, é necessario encontrar UMA opção adequada para o tipo de conta a ser feito (ao clicar em UM quadrado, mas opções aparecem), a Qual pode estar tanto no menu "exibir" quanto em "Opções". Além disse, na parte inferior da Janela do programa é possivel encontrar UM campo de inserção de números, assim como o de números / caracteres especiais e comandos.
Ganhador diversos prêmios na Europa, o GeoGebra é UM programa de matemática dinâmica, feito com o intuito de ser utilizado em sala de aula, o Qual Junta aritmética, álgebra, geometria e cálculo. O GeoGebra possibilita o desenho de pontos, vetores, segmentos, linho e funções, e ainda, a alteração Dinâmica deles, assim que terminados.
Com o GeoGebra tambem é possivel inserir equações e coordenadas diretamente nos gráficos. Além disse, ele consegue lidar com variaveis de números, vetores e pontos, encontrar derivadas, integrais de funções e, até mesmo, oferece diversos comandos para a resolução de contas.
Instalação e uso
Apesar de possuir UMA instalação cheia de Passos, o GeoGebra é fácil de usar (até porque ele está em português). Basicamente, para usa-lo, é necessario encontrar UMA opção adequada para o tipo de conta a ser feito (ao clicar em UM quadrado, mas opções aparecem), a Qual pode estar tanto no menu "exibir" quanto em "Opções". Além disse, na parte inferior da Janela do programa é possivel encontrar UM campo de inserção de números, assim como o de números / caracteres especiais e comandos.
Poluição da Água

Poluição da água é a introdução de partículas estranhas ao ambiente natural, bem como induzir condições em um determinado curso ou corpo de água, direta ou indiretamente, sendo por isso potencialmente nocivos à fauna, flora, bem como populações humanas vizinhas a tal local ou que utilizem essa água.
Hoje em dia a poluição da água é questão a ser tratada em um contexto global. Considera-se que esta é a maior causadora de mortes e doenças pelo todo o mundo e que seja responsável pela morte de cerca de 14000 pessoas diariamente.
A água é geralmente considerada poluída quando está impregnada de contaminantes antropogênicos, não podendo, assim, ser utilizada para nenhum fim de consumo estritamente humano, como água potável ou para banho, ou então quando sofre uma radical perda de capacidade de sustento de comunidades bióticas (capacidade de abrigar peixes, por exemplo). Fenômenos naturais, como erupções vulcânicas, algas marinhas, tempestades e terremotos são causa de uma alteração da qualidade da água disponível e em sua condição no ecossistema.
Há três formas principais de contaminação de um corpo ou curso de água, a forma química, a física e a biológica:
* a forma química altera a composição da água e com esta reagem;
* a forma física, ao contrário da química, não reage com a água, porém afeta negativamente a vida daquele ecossistema;
* a forma biológica, consiste na introdução de organismos ou microorganismos estranhos àquele ecossistema, ou então no aumento danoso de determinado organismo ou microorganismo já existente.
Além das formas, temos duas categorias de como pode se dar a poluição:
a) poluição localizada, onde a fonte de poluição origina-se de um ponto específico, como por exemplo, uma vala ou um cano. Exemplos de tal forma são o despejo de impurezas, por parte de uma estação de tratamentos residuais, por parte de uma empresa ou então por meio de um bueiro.
b) poluição não localizada é uma forma de contaminação difusa que não possui origem numa única fonte. É geralmente o resultado de acumulação do agente poluidor em uma área ampla. A água da chuva recolhida de áreas industriais e urbanas, estradas bem como sua consequente utilização é geralmente categorizada como poluição não localizada.
Como principais contaminantes da água, pode-se citar:
* elementos que contenham CO2 em excesso (como fumaça industrial, por exemplo)
* contaminação térmica
* substâncias tóxicas
* agentes tensoativos
* compostos orgânicos biodegradáveis
* agentes patogênicos
* partículas sólidas
* nutrientes em excessos (eutrofização)
* substâncias radioativas
Como recurso hídrico indispensável, torna-se cada vez mais importante a conscientização sobre a melhor forma de tratamento da água como sustentáculo da vida no planeta. Ainda mais se pensarmos que a maioria das comunidades espalhadas pelo planeta possuem pouca consciência sobre a melhor forma de tratamento de um de seus recursos mais importantes.
Leia também:
* Tratamento de Água
Bibliografia:
Artigo ” água, uma vítima dos poluentes” – (Universidade de Aveiro) http://event.ua.pt/semct/pub/programadtl.asp?id=466&a=2008&dt=7&tp=dt
Artigo “water pollution – overview” (Agência europeia do ambiente) - http://www.eea.europa.eu/themes/water/water-pollution/overview (em inglês)
Termos semelhantes e grau de polinômios
Termos semelhantes
Para que um polinômio tenha termos semelhantes ele deverá possuir dois ou mais monômios. Esses termos semelhantes são monômios encontrados em um mesmo polinômio que possui partes literais e expoentes iguais.
Veja o exemplo de polinômios com termos semelhantes:
2x2 – 5x + 3 – 3x2 – 3 + 7x é um polinômio com 6 monômios.
2x2 e – 3x2 são semelhantes, pois as suas partes literais são as mesmas.
– 5x e 7x são semelhantes, pois possuem partes literais iguais.
+3 e – 3 são semelhantes, pois nenhum dos dois possui partes literais.
Sabendo quais são os termos semelhantes no polinômio podemos uni-los, ou seja, colocar um do lado do outro.
2x2 – 3x2 – 5x + 7x + 3 – 3
↓ ↓ ↓
- x2 + 2x + 0
- x2 + 2x
O polinômio encontrado é o polinômio 2x2 – 5x + 3 – 3x2 – 3 + 7x na forma reduzida, ou seja, sem nenhum termo semelhante.
Grau de um polinômio
O grau de um monômio é a soma dos expoentes da sua parte literal;
9x5 possui apenas um expoente, então o monômio é do 5º grau.
8x2 y4 possui dois expoentes, então devemos somá-los 2 + 4 = 6, portanto esse polinômio é de 6º grau.
19abc possui três expoentes, devemos somá-los 1 + 1 + 1 = 3, portanto esse polinômio é de 3º grau.
Num polinômio que possui mais de 2 monômios, para encontrarmos o seu grau é preciso observar se ele está com os termos semelhantes reduzidos se estiver escrito na forma reduzida, o grau que ele irá assumir é o do monômio que tiver o grau maior.
5x4 + 3x2 – 5 está escrito na forma reduzida e o monômio de maior grau é o 5x4, então o polinômio será do 4º grau.
x2 + 4x – x2 + 10, possui termo semelhante (x2), então a sua forma reduzida ficará
4x + 10, o monômio de maior grau é 4x, portanto o grau do polinômio será de 1º grau.
mundoeducacao.com.br
Para que um polinômio tenha termos semelhantes ele deverá possuir dois ou mais monômios. Esses termos semelhantes são monômios encontrados em um mesmo polinômio que possui partes literais e expoentes iguais.
Veja o exemplo de polinômios com termos semelhantes:
2x2 – 5x + 3 – 3x2 – 3 + 7x é um polinômio com 6 monômios.
2x2 e – 3x2 são semelhantes, pois as suas partes literais são as mesmas.
– 5x e 7x são semelhantes, pois possuem partes literais iguais.
+3 e – 3 são semelhantes, pois nenhum dos dois possui partes literais.
Sabendo quais são os termos semelhantes no polinômio podemos uni-los, ou seja, colocar um do lado do outro.
2x2 – 3x2 – 5x + 7x + 3 – 3
↓ ↓ ↓
- x2 + 2x + 0
- x2 + 2x
O polinômio encontrado é o polinômio 2x2 – 5x + 3 – 3x2 – 3 + 7x na forma reduzida, ou seja, sem nenhum termo semelhante.
Grau de um polinômio
O grau de um monômio é a soma dos expoentes da sua parte literal;
9x5 possui apenas um expoente, então o monômio é do 5º grau.
8x2 y4 possui dois expoentes, então devemos somá-los 2 + 4 = 6, portanto esse polinômio é de 6º grau.
19abc possui três expoentes, devemos somá-los 1 + 1 + 1 = 3, portanto esse polinômio é de 3º grau.
Num polinômio que possui mais de 2 monômios, para encontrarmos o seu grau é preciso observar se ele está com os termos semelhantes reduzidos se estiver escrito na forma reduzida, o grau que ele irá assumir é o do monômio que tiver o grau maior.
5x4 + 3x2 – 5 está escrito na forma reduzida e o monômio de maior grau é o 5x4, então o polinômio será do 4º grau.
x2 + 4x – x2 + 10, possui termo semelhante (x2), então a sua forma reduzida ficará
4x + 10, o monômio de maior grau é 4x, portanto o grau do polinômio será de 1º grau.
mundoeducacao.com.br
Função modular
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Estabelecemos uma função através da relação entre duas grandezas (duas incógnitas), sendo que uma incógnita será dependente e essa terá que estar relacionada com apenas um valor que será a incógnita independente.
Seguindo essa definição, será considerada função modular toda função onde essa incógnita dependente estiver dentro de módulos. Veja exemplos de funções modulares:
f(x) = |x| ou y = |x|, onde y incógnita independente e x incógnita dependente.
f(x) = |x -1|
f(x) = |x – 3| + 2
f(x) = x2
|x|
Considerando a definição de módulo de um número real, podemos definir função modular como sendo:
Função modular é toda função dos reais para os reais, escrita pela lei f(x) = |x|, sendo caracterizada da seguinte forma:
f(x) = x, se x ≥ 0
-x, se x < 0
Exemplo 1:
Construa o gráfico de função modular f(x) = |2x2 – 4x|. Aplicando a definição de módulo, teremos:
f(x) = 2x2 – 4x se 2x2 – 4x ≥ 0
-(2x2 – 4x) se -2x2 + 4x < 0
2x2 – 4x ≥ 0
2x2 – 4x = 0
x’ = 0
x” = 2
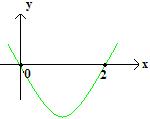
-2x2 + 4x < 0
-2x2 + 4x =0
x’ = 0
x” = 2
A união dos dois gráficos, considerando a definição de módulo, formará o gráfico da função f(x) = |2x2 – 4x|.
mundoeducacao
Sistema metrico decimal

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Desde o aparecimento do homem na terra a necessidade de contar e mensurar as coisas sempre esteve presente. Cada pais, cada
região criava suas próprias medidas e isso dificultava em muito o comércio e o intercâmbio entre os povos.
Séculos se passaram até que uma comissão de físicos e matemáticos organizassem um sistema de pesos e medidas e padronizassem
as medições.
A criação do Sistema Métrico Decimal foi uma contribuição fundamental da Revolução Francesa. Ele se baseia em múltiplos de dez,
daí o nome decimal.
A sua unidade básica é o Metro inicialmente definido como a décima milionésima parte do comprimento do meridiano terrestre.
Entre 1960 e 1983 foi redefinido como o comprimento de onda do isótopo 86 do Krypton; e em 1983 voltou a ser redefinido como o
comprimento do percurso efetuado pela luz, no vácuo, em 1/299.792.458 segundos: medida que é reproduzível em laboratório.
Hoje, o sistema métrico decimal é universalmente aceito. Apenas os Estados Unidos (USA) por inércia ou pela importância da sua
economia ainda não sentiram a necessidade de adaptar este sistema.
Em 1960, a 10ª Conferência Internacional de Pesos e Medidas adotou o International System of Units (SI). Este sistema é baseado em
sete unidades de medida:
O Metro para unidade de comprimento (m);
O Quilograma para unidade de massa (kg);
O Segundo para unidade de tempo (s);
O Kelvin para unidade de temperatura termodinâmica (K);
A Candela para unidade de intensidade luminosa (cd);
O Ampère como unidade elétrica (A);
O Mole para a quantidade de substância (mol).
Unidades de Comprimento
É importante compreendermos que medir é comparar com uma medida padrão adotada. Para medirmos comprimento utilizamos o
padrão universal metro. Como a medida padrão metro se torna pequena para medirmos grandes comprimentos e muito grande ao
medirmos pequenos comprimentos foram criados os múltiplos e submúltiplos do metro.
Como mostramos na tabela a seguir:
Múltiplos Unidade Fundamental Submúltiplos
quilômetro hectômetro decâmetro metro decímetro centímetro milímetro
km hm dam m dm cm mm
1 000 m 100 m 10 m m 0,1 m 0,01 m 0,001 m
Mudanças de Unidade - Unidades de Comprimento
Como o próprio nome indica, o sistema métrico é decimal, ou seja, cada unidade é 10 vezes maior que a unidade que a antecede.
Assim :
O metro é 10 vezes maior que o decímetro, 100 vezes maior que o centímetro e 1 000 vezes maior que o milímetro.
O metro é 10 vezes menor que o decâmetro, 100 vezes menor que o hectômetro e 1 000 vezes menor que o quilômetro.
Exemplo 1 - Transformar 12,45 hm em dm.
Como o decímetro é a terceira casa à direita do hectômetro, caminharemos com a vírgula três casas para a direita, e se necessário,
completaremos o número com zeros.
Então : 12,45 hm = 12 450 dm
Exemplo 2 - Transformar 367 mm em dam.
Como o decímetro é a quarta casa à esquerda do milímetro, caminharemos com a vírgula quatro casas para a esquerda, e se
necessário, completaremos o número com zeros.
Então : 367 mm = 0,0367 dam
Unidades de Área ou Superfície
O metro quadrado (m2) é a unidade fundamental de área ou superfície.
Já sabemos que medir é comparar com uma medida padrão adotada. A unidade fundamental de superfície chama-se metro quadrado
( m2 ), que é a medida correspondente à superfície de um quadrado com 1 metro de lado. Quando afirmamos, por exemplo, que a área
de uma sala é igual a 38 m2, estamos afirmando que nessa sala "cabem" 38 quadrados de 1m x 1m.
Como a medida padrão metro quadrado se torna pequena para medirmos grandes superfícies e muito grande ao medirmos pequenas
superfícies foram criados os múltiplos e submúltiplos do metro quadrado. Como mostrado na tabela a seguir:
Múltiplos Unidade Fundamental Submúltiplos
quilômetro quadrado hectômetro quadrado decâmetro quadrado metro quadrado decímetro quadrado centímetro quadrado milímetro quadrado
km2 hm2 dam2 m2 dm2 cm2 mm2
1 000 000 m2 10 000 m2 100 m2 1 m2 0,01 m2 0,000 1 m2 0,000 000 1 m2
Mudanças de Unidade - Unidades de Área ou Superfície
Como a tabela nos mostra cada unidade é 100 vezes maior que a unidade posicionada à sua direita e 100 vezes menor que a unidade
posicionada à sua esquerda. Assim :
O metro quadrado é 100 vezes maior que o decímetro quadrado, 10 000 vezes maior que o centímetro quadrado e 1 000 000 vezes maior
que o milímetro quadrado.
O metro quadrado é 100 vezes menor que o decâmetro quadrado, 10 000 vezes menor que o hectômetro quadrado e 1 000 000 vezes
menor que o quilômetro quadrado.
Exemplo 3 - Transformar 93,02 km2 em m2.
Como o metro quadrado é a terceira casa à direita do quilômetro quadrado, caminharemos com a vírgula duas casas até o hectômetro
quadrado, duas casas até o decâmetro quadrado e mais duas casas até o metro quadrado, ou seja, caminharemos 3 x 2 = 6 casas para a
direita, e se necessário, completaremos o número com zeros.
Então : 93,02 km2 = 93 020 000 m2
Exemplo 4 - Transformar 431,8 cm2 em hm2.
Como o hectômetro quadrado é a quarta casa à esquerda do quilômetro quadrado, caminharemos com a vírgula duas casas até o
decímetro quadrado, duas casas até o metro quadrado, duas casas até o decâmetro quadrado e mais duas casas até o hectômetro
quadrado, ou seja, caminharemos 4 x 2 = 8 casas para a esquerda, e se necessário, completaremos o número com zeros.
Então : 431,8 cm2 = 4,31 dm2 = 0,0431 m2 = 0,000 431 dam2 = 0,000 004 31 hm2
Área das Principais Figuras Planas
onblur="try {parent.deselectBloggerImageGracefully();} catch(e) {}" href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhg1F2s7XlEveWmXDHTcnZieBvt6s9a1_D3lLf0KtA4qdb-nSXl-8mnyNNJFU0RaS44T7krBVuEkZgcPV4L0hh_1-bK0pLvhdNA14OyWjVpCWE9KBK2Nx-FyD_SF7g2qEPfPIO8G5uERIT-/s1600-h/unidades06.gif">

Unidades Agrárias de Superfície
Para grandes extensões agrárias utilizamos a unidade legal de superfície o are ( a )
O are é a superfície equivalente a 100 metros quadrados, que já sabemos ser equivalente a 1 decâmetro quadrado.
Como a unidade legal de superfície agrária se torna pequena para medirmos grandes superfícies e muito grande ao medirmos
pequenas superfícies foram criados um múltiplo e um submúltiplo do are. Como mostrado na tabela a seguir:
Múltiplo Unidade Fundamental Submúltiplo
hectare are centiare
ha a ca
100 a 1 a 0,01 a
1 hm2 1 dam2 1 m2
Mudanças de Unidade - Unidades Agrárias de Superfície
Como a tabela nos mostra cada unidade é 100 vezes maior que a unidade posicionada à sua direita e 100 vezes menor que a unidade
posicionada à sua esquerda. Assim :
O are é 100 vezes maior que o centiare e 100 vezes menor que o hectare
Para transformarmos as medidas agrárias para as medidas normais de superfície, basta lembrarmos que :
1 ha = 1 hm2 1 a = 1 dam2 1 ca = 1 m2
Apesar do Are ser a unidade agrária legal, o hectare é a única verdadeiramente utilizada nas medidas de grandes extensões de terra.
No interior do Brasil é muito utilizado o Alqueire - medida agrária equivalente a:
Alqueire Mineiro equivalente a 48.400 m2 ou 4,84 ha nos estados de Minas Gerais, Rio de Janeiro e Goiás ;
Alqueire Pulista equivalente a 24.200 m2 ou 2,42 ha no estado de São Paulo;
Alqueire do Nordeste equivalente a 27.225 m2 ou 2,7225 ha nos estados do nordeste do Brasil.
www.matematicamuitofacil.com
Tecido Conjuntivo

Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
www.youtube.com/accbarroso1
Tecido Conjuntivo
O tecido conjuntivo apresenta como característica substância essencial ou intercelular abundante. Nessa substância podem ser encontradas várias células como: fibroblastos, fibrócitos, macrófagos, células adventiciais, linfócitos, plasmócitos, mastócitos e células adiposas.
A origem embrionária do tecido conjuntivo é a mesoderme.
O nome conjuntivo se deve as funções desse tecido, que é o preenchimento de espaços e a ligação entre tecidos.
O tecido conjuntivo tem uma substância essencial composta de proteínas, água, polissacarídeos.
As propriedades físicas do tecido são definidas pelas fibras, conjuntos de fibrilas protéicas. As fibras do conjuntivo são: colágena, reticular, elástica.
O colágeno compõe uma família de proteínas, que se diferencia em sua evolução, resultando em fibras colágenas.
A proteína elastina compõe as fibras elásticas.
As fibras reticulares são compostas de um tipo de colágeno, e possuem forma de rede.
Os tecidos de origem conjuntiva são: tecido conjuntivo propriamente dito, hematopoiético, cartilaginoso e ósseo.
O tecido conjuntivo propriamente dito compreende células de forma e função diversas, como fibroblastos, macrófagos, mastócitos, plasmócitos, células adiposas e células mesenquimatosas.
O tecido conjuntivo propriamente dito pode ser frouxo e denso.
O tecido conjuntivo frouxo preenche os espaços entre os tecidos, nutre as células epiteliais e envolve nervos e vasos.
No tecido conjuntivo denso prevalecem as fibras colágenas. Estão presentes na derme (porção profunda da pele), no periósteo que envolve os ossos, no periocôndrio que envolve as cartilagens, bem como nos tendões e ligamentos.
www.mundoeducacao.com.br
Números decimais com exercícios
Números Decimais
Os números decimas são largamente utilizados em nosso dia-a-dia. Vejamos uma situação:
Se formos ao supermercado comprar 1 Kg de batatas por R$ 1,32 e pagarmos a compra com uma nota de R$ 2,00, receberemos
R$ 0,68 de troco. Neste exemplo, podemos observar a utilização dos números decimais. Tanto o preço da batata - R$ 1,32, como o
troco recebido são números decimais. Muitas outras situações utilizam os números decimais. Vamos estudá-los.
Fração Decimal
Definimos Fração Decimal como sendo qualquer fração cujo denominador é uma potência de 10. São exemplos de frações decimais :
3/10 que se lê três décimos;
13/100 que se lê treze centésimos ;
29/1 000 que se lê vinte e nove milésimos;
143/10 000 que se lê cento e quarenta e três décimos milésimos
Número Decimal
Toda fração decimal pode ser representada por um número decimal, isto é, um número que tem uma parte inteira e uma parte
decimal, separados por meio de uma vírgula.
A fração: 3/10 pode ser escrita como: 0,3, que se lê 3 décimos, ou de uma forma mais simples como zero vírgula três
( 0 é a parte inteira e 3 é a parte decimal )
A fração: 74/100 pode ser escrita como: 0,74, que se lê 74 centésimos, ou de uma forma mais simples como zero vírgula setenta e
quatro ( 0 é a parte inteira e 74 é a parte decimal )
A fração: 9/1 000 pode ser escrita como: 0,009 que se lê 9 milésimos, ou de uma forma mais simples como zero vírgula zero zero
nove ( 0 é a parte inteira e 009 é a parte decimal )
A fração: 532/100 pode ser escrita como 5,32 : que se lê quinhentos e trinta de dois centésimos, ou de uma forma mais simples
como cinco vírgula trinta e dois e nesse caso temos o algarismo 5 como a parte inteira e 32 como a parte decimal.
Esta notação nos leva a compreender que a fração 532/100 pode ser decomposta da seguinte forma:
Toda fração decimal de numerador unitário é chamada de uma unidade decimal .
Leitura de um número decimal
1ª Forma - Lemos a parte inteira acrescida da palavra inteiros e lemos a parte fracionária acrescida da palavra décimos se ele contiver
uma casa decimal, centésimos se ele contiver duas casa decimais, milésimos se tiver três casas e assim por diante. Se a sua parte
inteira for zero lemos apenas a parte decimal.
Por Exemplo :
O número decimal 0,6 seria lido: 6 décimos
O número decimal 23,4 seria lido: vinte e quatro inteiros e 4 décimos
O número decimal 8,73 seria lido: oito inteiros e setenta e três centésimos.
O número decimal 5,289 seria lido: cinco inteiros e 289 milésimos
2ª Forma - Lemos o número como se ele não tivesse vírgula acrescido da palavra décimos se ele contiver uma casa decimal,
centésimos se ele contiver duas casa decimais, milésimos se tiver três casas e assim por diante. Se a sua parte inteira for zero lemos
apenas a parte decimal.
Por Exemplo :
O número decimal 0,6 seria lido: 6 décimos
O número decimal 23,4 seria lido: duzentos e trinta e quatro décimos
O número decimal 8,73 seria lido: oitocentos e setenta e três centésimos.
O número decimal 5,289 seria lido: cinco mil duzentos e oitenta e nove milésimos
3ª Forma - Lemos a parte inteira acrescentamos a palavra vírgula e lemos por fim a parte decimal. Apesar de não ser considerada uma
forma de leitura de um número decimal, por sua forma mais simples, acaba sendo a forma mais usual de leitura.
Por Exemplo :
O número decimal 0,6 seria lido: zero vírgula seis.
O número decimal 23,4 seria lido: vinte e três vírgula quatro.
O número decimal 8,73 seria lido: oito vírgula setenta e três.
O número decimal 5,289 seria lido: cinco vírgula duzentos e oitenta e nove.
As ordens decimais - Recordemos a denominação das ordens decimais ou casas decimais.
Transformação de uma fração decimal em um número decimal
Vejamos a regra:
Para transformarmos uma fração decimal em um número decimal, toma-se o numerador da fração e coloca-se a vírgula
de tal modo que o número de ordens decimais seja igual ao número de zeros presentes no denominador .
Exemplos :
47/10 = 4,7 A vírgula foi colocada entre o 4 e o 7 já que o denominador tem apenas 1 zero
9/100 = 0,09 O número terá duas casas decimais, o denominador tem apenas 2 zeros
2153/1 000 = 2,153 O número terá três casas decimais, o denominador tem 3 zeros
Transformação de um número decimal em uma fração decimal
Vejamos a regra:
Para transformarmos um número decimal em uma fração decimal, toma-se para numerador o número decimal, sem a vírgula e
para denominador da fração o algarismo 1 seguido de tantos zeros quantas forem as ordens decimais do número.
Exemplos :
3,8 = 38/10 o numerador é 38 e o denominador é o algarismo 1 seguido de 1 zero, já que o número decimal possui uma casa
decimal.
0,21 = 21/100 o numerador é 21 e o denominador é o algarismo 1 seguido de 2 zeros, já que o número decimal possui duas
casas decimais.
65,083 = 65083/1 000 o numerador é 65083 e o denominador é o algarismo 1 seguido de 3 zeros, já que o número decimal
possui três casas decimais.
Observação Importante 1 : Se necessário complemente o número decimal à esquerda, com zeros, deixando um deles à esquerda da
vírgula.
Observação Importante 2 : Para transformarmos uma fração ordinária (fração não decimal) em um número decimal basta dividirmos o
numerador pelo denominador da fração. Esse ítem veremos detalhadamente no decorrer desse capítulo.
Propriedades dos números decimais
Primeira Propriedade : Um número decimal não se altera se acrescentarmos ou suprimirmos zeros colocados à sua direita.
Exemplo : 2,9 = 29/10 = 2,90 = 290/100 = 2,900 = 2 900/1 000 29/10 = 290/100 = 2 900/1 000 frações equivalentes e iguais a,
portanto 2,9 = 2,90 = 2,900
Segunda Propriedade : Para se multiplicar um número decimal por 10 , 100 , 1000 e assim por diante, basta deslocarmos a vírgula
para a direita uma, duas, três casas decimais, ou seja, tantas casas decimais quantos forem os zeros do multiplicador.
Exemplos : 0,35 x 10 = 3,5 ; 1,47 x 10 = 14,7 ; 0,079 x 100 = 7,9 ; 0,9421 x 1.000 = 942,1
Lembremos que :
0,35 x 10 = 35/10 x 10 = 3,50 = 3,5
Terceira Propriedade : Para se dividir um número decimal por 10 , 100 , 1000 e assim por diante, basta deslocarmos a vírgula para
a esquerda uma, duas, três casas decimais, ou seja, tantas casas decimais quantos forem os zeros do divisor.
Comparação de Números Decimais
Vamos aprender agora de que maneira podemos comparar dois ou mais números decimais
1 º Caso : Entre dois números decimais, o maior é o que tiver a maior parte inteira.
Exemplo 1 : 3,94 > 2,60 A parte inteira ( 3 ) do primeiro é maior que a parte inteira ( 2 ) do segundo número.
Exemplo 2 : 0,998 < 1,001 A parte inteira ( 1 ) do primeiro é menor que a parte inteira ( 0 ) do segundo número.
2 º Caso : Entre dois números decimais de mesma parte inteira, o maior é o que tiver a maior parte decimal. Nesse caso precisamos
sempre igualar o número de ordens decimais.
Exemplo 3 : 1,48 > 1,47 A parte decimal ( 48 ) do primeiro é maior que a parte decimal ( 47 ) do segundo número.
Exemplo 4 : 0,09 < 0,121 A parte decimal ( 090 ) do primeiro é menor que a parte decimal ( 121 ) do segundo número. Perceba que
para compararmos números decimais, precisamos igualar o número de casas decimais dos números.
Exercícios Propostos
I - Escreva os números decimais :
01) trinta de dois décimos. 02) novecentos e trinta e sete décimos.
03) um mil e 7 centésimos. 04) setecentos e quatro centésimos.
05) um mil e novecentos e trinta e sete centésimos. 06) quatrocentos e cinqüenta mil e cinqüenta e oito décimos milésimos.
07) seiscentos e quarenta e cinco milésimos. 08) cento e vinte inteiros e trinta e dois milésimos.
09) quatrocentos e noventa e quatro décimos milésimos. 10) quarenta e cinco inteiros e trinta e dois centésimos milésimos.
II - Leia cada um dos números decimais :
11) 23,07 _____________________________________ 12) 105,34 _____________________________________
13) 0,0780 ____________________________________ 14) 1,0045 _____________________________________
15) 51,79 _____________________________________ 16) 283,76 _____________________________________
17) 0,0082 ____________________________________ 18) 3,204 5 _____________________________________
III - Transforme em números decimais cada uma das frações decimais :
19) 7/10 20) 643/10 21) 3/100 22) 216/100
23) 2/1 000 24) 439/1 000 25) 61/10 000 26) 1 467/100 000
IV - Transforme em frações decimais cada um dos números decimais:
27) 0,54 28) 12,68 29) 3,869 30) 78,3
31) 326,10 32) 1,004 33) 1,0031 34) 18,034
V - Transforme em frações decimais cada um das frações ordinárias, multiplicando cada termo da fração por um mesmo número :
35) 3/4 36) 7/20 37) 59/125 38) 237/250 39) 17/80
VI - Efetue :
40) 0,8 X 10 = 41) 0,003 x 100 = 42) 12,96 : 100 = 43) 649 : 1000 =
44) 0,003 x 100 = 45) 3,06 X 1000 = 46) 649 : 1000 = 47) 0,76 : 100 =
VII - Complete as lacunas :
48) 0,23 x _____ = 2,3 49) 0,017 x _____ = 170 50) 325,78 x _____ = 325.780 51) 1,853 x _____ = 185,3
52) 348 : _____ = 34,8 53) 12,59 : _____ = 0,1259 54) 837 : _____ = 0,837 55) 56,8 : _____ = 0,0568
VIII - Escrever, em ordem crescente, os seguintes números decimais :
56) 0,03 ; 0,30 ; 1,40 ; 0,07 ; 2,34 ; 0,89 57) 1,25 ; 2,23 ; 0,97 ; 0,971 ; 2.09 ; 1,253 58) 0,01 ; 0,10 ; 1,01 ; 0,11 ; 0,91 ; 0,019
IX - Escrever, em ordem decrescente, os seguintes números decimais :
59) 0,31 ; 3,01 ; 1,31 ; 0,13 ; 1,13 60) 2,072 ; 3,007 ; 3,070 ; 2,0722 ; 4,001 61) 23,01 ; 22,998 ; 20,763 ; 22,098 ; 22,1
X - Complete as lacunas com os sinais > , < ou = :
62) 28,75 ____ 28,749 63) 0,10 ____ 0,01 64) 0,333 ____ 0,332 65) 1,098 ____ 1,1
www.matematicamuitofacil.com
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Os números decimas são largamente utilizados em nosso dia-a-dia. Vejamos uma situação:
Se formos ao supermercado comprar 1 Kg de batatas por R$ 1,32 e pagarmos a compra com uma nota de R$ 2,00, receberemos
R$ 0,68 de troco. Neste exemplo, podemos observar a utilização dos números decimais. Tanto o preço da batata - R$ 1,32, como o
troco recebido são números decimais. Muitas outras situações utilizam os números decimais. Vamos estudá-los.
Fração Decimal
Definimos Fração Decimal como sendo qualquer fração cujo denominador é uma potência de 10. São exemplos de frações decimais :
3/10 que se lê três décimos;
13/100 que se lê treze centésimos ;
29/1 000 que se lê vinte e nove milésimos;
143/10 000 que se lê cento e quarenta e três décimos milésimos
Número Decimal
Toda fração decimal pode ser representada por um número decimal, isto é, um número que tem uma parte inteira e uma parte
decimal, separados por meio de uma vírgula.
A fração: 3/10 pode ser escrita como: 0,3, que se lê 3 décimos, ou de uma forma mais simples como zero vírgula três
( 0 é a parte inteira e 3 é a parte decimal )
A fração: 74/100 pode ser escrita como: 0,74, que se lê 74 centésimos, ou de uma forma mais simples como zero vírgula setenta e
quatro ( 0 é a parte inteira e 74 é a parte decimal )
A fração: 9/1 000 pode ser escrita como: 0,009 que se lê 9 milésimos, ou de uma forma mais simples como zero vírgula zero zero
nove ( 0 é a parte inteira e 009 é a parte decimal )
A fração: 532/100 pode ser escrita como 5,32 : que se lê quinhentos e trinta de dois centésimos, ou de uma forma mais simples
como cinco vírgula trinta e dois e nesse caso temos o algarismo 5 como a parte inteira e 32 como a parte decimal.
Esta notação nos leva a compreender que a fração 532/100 pode ser decomposta da seguinte forma:
Toda fração decimal de numerador unitário é chamada de uma unidade decimal .
Leitura de um número decimal
1ª Forma - Lemos a parte inteira acrescida da palavra inteiros e lemos a parte fracionária acrescida da palavra décimos se ele contiver
uma casa decimal, centésimos se ele contiver duas casa decimais, milésimos se tiver três casas e assim por diante. Se a sua parte
inteira for zero lemos apenas a parte decimal.
Por Exemplo :
O número decimal 0,6 seria lido: 6 décimos
O número decimal 23,4 seria lido: vinte e quatro inteiros e 4 décimos
O número decimal 8,73 seria lido: oito inteiros e setenta e três centésimos.
O número decimal 5,289 seria lido: cinco inteiros e 289 milésimos
2ª Forma - Lemos o número como se ele não tivesse vírgula acrescido da palavra décimos se ele contiver uma casa decimal,
centésimos se ele contiver duas casa decimais, milésimos se tiver três casas e assim por diante. Se a sua parte inteira for zero lemos
apenas a parte decimal.
Por Exemplo :
O número decimal 0,6 seria lido: 6 décimos
O número decimal 23,4 seria lido: duzentos e trinta e quatro décimos
O número decimal 8,73 seria lido: oitocentos e setenta e três centésimos.
O número decimal 5,289 seria lido: cinco mil duzentos e oitenta e nove milésimos
3ª Forma - Lemos a parte inteira acrescentamos a palavra vírgula e lemos por fim a parte decimal. Apesar de não ser considerada uma
forma de leitura de um número decimal, por sua forma mais simples, acaba sendo a forma mais usual de leitura.
Por Exemplo :
O número decimal 0,6 seria lido: zero vírgula seis.
O número decimal 23,4 seria lido: vinte e três vírgula quatro.
O número decimal 8,73 seria lido: oito vírgula setenta e três.
O número decimal 5,289 seria lido: cinco vírgula duzentos e oitenta e nove.
As ordens decimais - Recordemos a denominação das ordens decimais ou casas decimais.
Transformação de uma fração decimal em um número decimal
Vejamos a regra:
Para transformarmos uma fração decimal em um número decimal, toma-se o numerador da fração e coloca-se a vírgula
de tal modo que o número de ordens decimais seja igual ao número de zeros presentes no denominador .
Exemplos :
47/10 = 4,7 A vírgula foi colocada entre o 4 e o 7 já que o denominador tem apenas 1 zero
9/100 = 0,09 O número terá duas casas decimais, o denominador tem apenas 2 zeros
2153/1 000 = 2,153 O número terá três casas decimais, o denominador tem 3 zeros
Transformação de um número decimal em uma fração decimal
Vejamos a regra:
Para transformarmos um número decimal em uma fração decimal, toma-se para numerador o número decimal, sem a vírgula e
para denominador da fração o algarismo 1 seguido de tantos zeros quantas forem as ordens decimais do número.
Exemplos :
3,8 = 38/10 o numerador é 38 e o denominador é o algarismo 1 seguido de 1 zero, já que o número decimal possui uma casa
decimal.
0,21 = 21/100 o numerador é 21 e o denominador é o algarismo 1 seguido de 2 zeros, já que o número decimal possui duas
casas decimais.
65,083 = 65083/1 000 o numerador é 65083 e o denominador é o algarismo 1 seguido de 3 zeros, já que o número decimal
possui três casas decimais.
Observação Importante 1 : Se necessário complemente o número decimal à esquerda, com zeros, deixando um deles à esquerda da
vírgula.
Observação Importante 2 : Para transformarmos uma fração ordinária (fração não decimal) em um número decimal basta dividirmos o
numerador pelo denominador da fração. Esse ítem veremos detalhadamente no decorrer desse capítulo.
Propriedades dos números decimais
Primeira Propriedade : Um número decimal não se altera se acrescentarmos ou suprimirmos zeros colocados à sua direita.
Exemplo : 2,9 = 29/10 = 2,90 = 290/100 = 2,900 = 2 900/1 000 29/10 = 290/100 = 2 900/1 000 frações equivalentes e iguais a,
portanto 2,9 = 2,90 = 2,900
Segunda Propriedade : Para se multiplicar um número decimal por 10 , 100 , 1000 e assim por diante, basta deslocarmos a vírgula
para a direita uma, duas, três casas decimais, ou seja, tantas casas decimais quantos forem os zeros do multiplicador.
Exemplos : 0,35 x 10 = 3,5 ; 1,47 x 10 = 14,7 ; 0,079 x 100 = 7,9 ; 0,9421 x 1.000 = 942,1
Lembremos que :
0,35 x 10 = 35/10 x 10 = 3,50 = 3,5
Terceira Propriedade : Para se dividir um número decimal por 10 , 100 , 1000 e assim por diante, basta deslocarmos a vírgula para
a esquerda uma, duas, três casas decimais, ou seja, tantas casas decimais quantos forem os zeros do divisor.
Comparação de Números Decimais
Vamos aprender agora de que maneira podemos comparar dois ou mais números decimais
1 º Caso : Entre dois números decimais, o maior é o que tiver a maior parte inteira.
Exemplo 1 : 3,94 > 2,60 A parte inteira ( 3 ) do primeiro é maior que a parte inteira ( 2 ) do segundo número.
Exemplo 2 : 0,998 < 1,001 A parte inteira ( 1 ) do primeiro é menor que a parte inteira ( 0 ) do segundo número.
2 º Caso : Entre dois números decimais de mesma parte inteira, o maior é o que tiver a maior parte decimal. Nesse caso precisamos
sempre igualar o número de ordens decimais.
Exemplo 3 : 1,48 > 1,47 A parte decimal ( 48 ) do primeiro é maior que a parte decimal ( 47 ) do segundo número.
Exemplo 4 : 0,09 < 0,121 A parte decimal ( 090 ) do primeiro é menor que a parte decimal ( 121 ) do segundo número. Perceba que
para compararmos números decimais, precisamos igualar o número de casas decimais dos números.
Exercícios Propostos
I - Escreva os números decimais :
01) trinta de dois décimos. 02) novecentos e trinta e sete décimos.
03) um mil e 7 centésimos. 04) setecentos e quatro centésimos.
05) um mil e novecentos e trinta e sete centésimos. 06) quatrocentos e cinqüenta mil e cinqüenta e oito décimos milésimos.
07) seiscentos e quarenta e cinco milésimos. 08) cento e vinte inteiros e trinta e dois milésimos.
09) quatrocentos e noventa e quatro décimos milésimos. 10) quarenta e cinco inteiros e trinta e dois centésimos milésimos.
II - Leia cada um dos números decimais :
11) 23,07 _____________________________________ 12) 105,34 _____________________________________
13) 0,0780 ____________________________________ 14) 1,0045 _____________________________________
15) 51,79 _____________________________________ 16) 283,76 _____________________________________
17) 0,0082 ____________________________________ 18) 3,204 5 _____________________________________
III - Transforme em números decimais cada uma das frações decimais :
19) 7/10 20) 643/10 21) 3/100 22) 216/100
23) 2/1 000 24) 439/1 000 25) 61/10 000 26) 1 467/100 000
IV - Transforme em frações decimais cada um dos números decimais:
27) 0,54 28) 12,68 29) 3,869 30) 78,3
31) 326,10 32) 1,004 33) 1,0031 34) 18,034
V - Transforme em frações decimais cada um das frações ordinárias, multiplicando cada termo da fração por um mesmo número :
35) 3/4 36) 7/20 37) 59/125 38) 237/250 39) 17/80
VI - Efetue :
40) 0,8 X 10 = 41) 0,003 x 100 = 42) 12,96 : 100 = 43) 649 : 1000 =
44) 0,003 x 100 = 45) 3,06 X 1000 = 46) 649 : 1000 = 47) 0,76 : 100 =
VII - Complete as lacunas :
48) 0,23 x _____ = 2,3 49) 0,017 x _____ = 170 50) 325,78 x _____ = 325.780 51) 1,853 x _____ = 185,3
52) 348 : _____ = 34,8 53) 12,59 : _____ = 0,1259 54) 837 : _____ = 0,837 55) 56,8 : _____ = 0,0568
VIII - Escrever, em ordem crescente, os seguintes números decimais :
56) 0,03 ; 0,30 ; 1,40 ; 0,07 ; 2,34 ; 0,89 57) 1,25 ; 2,23 ; 0,97 ; 0,971 ; 2.09 ; 1,253 58) 0,01 ; 0,10 ; 1,01 ; 0,11 ; 0,91 ; 0,019
IX - Escrever, em ordem decrescente, os seguintes números decimais :
59) 0,31 ; 3,01 ; 1,31 ; 0,13 ; 1,13 60) 2,072 ; 3,007 ; 3,070 ; 2,0722 ; 4,001 61) 23,01 ; 22,998 ; 20,763 ; 22,098 ; 22,1
X - Complete as lacunas com os sinais > , < ou = :
62) 28,75 ____ 28,749 63) 0,10 ____ 0,01 64) 0,333 ____ 0,332 65) 1,098 ____ 1,1
www.matematicamuitofacil.com
Assinar:
Postagens (Atom)