Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Hexágono é uma figura plana que possui 6 lados, sendo regular esses lados deverão ser todos iguais (mesma medida), portanto, hexágono regular é uma figura plana que possui 6 lados com a mesma medida.
O hexágono regular circunscrito numa circunferência irá dividi-lo em seis arcos de mesma medida, como o hexágono é regular os arcos formados irão medir 60° (360°: 6 = 60°). Cada lado irá formar com o centro um ângulo central que terá a mesma medida do arco, 60°.
Assim, podemos dizer que cada arco da circunferência irá formar com seu ângulo central seis triângulos eqüiláteros (triângulos com lados iguais) no hexágono regular.
Podemos dizer que a área de um hexágono regular será igual à soma das seis áreas dos triângulos eqüiláteros.
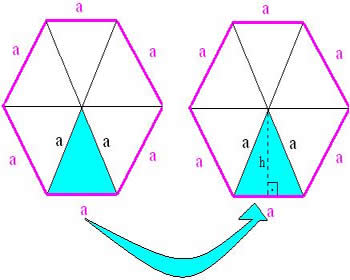
Calculando a área de um dos triângulos teremos:
A área de um triângulo é calculada utilizando a fórmula , portanto, temos que encontrar a altura.
Aplicando o Teorema de Pitágoras temos:
a2 = h2 + a2
4
a2 – a2 = h2
4
4a2 – a2 = h2
4
3a2 = h2
4
a√3 = h
2
Agora, substituindo o valor da base do triângulo, que é a, e o valor da altura.
Portanto, dizemos que a área do triângulo eqüilátero é:
A∆ = a . a√3
2
2
A∆ = a2 √3 . 1
2 2
A∆ = a2 √3
4
A área do hexágono regular será igual a 6 vezes a área do triângulo eqüilátero.
A = 6 . a2 √3
4
A = 3 a2 √3 2
mundoeducacao
Que blog incrível, vou aplicar essas dicas no colegio objetivo zona norte SP, adorei, recomendo
ResponderExcluir