Condição de alinhamento de três pontos

Marcelo Rigonatto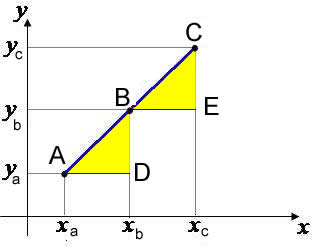

Pontos alinhados

Considere três pontos distintos do plano cartesiano A(x_a, y_a), B(x_b, y_b) e C(x_c, y_c). Esses pontos estão alinhados se o determinante de suas coordenadas for igual a zero. Ou seja:

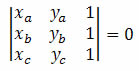
Exemplo 1. Verifique se os pontos A(5, 5), B(1, 3) e C(0, 5) estão alinhados.
Solução: devemos fazer o cálculo do determinante das coordenadas dos pontos A, B e C e verificar se o resultado é igual a zero.


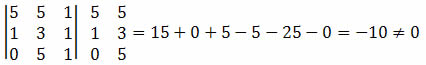
Como o determinante das coordenadas dos pontos resultou em um valor diferente de zero, podemos concluir que os pontos A, B e C não estão alinhados.

Exemplo 2. Determine o valor de c para que os pontos A(4, 2), B(2, 3) e C(0, c) estejam alinhados.
Solução: para que os pontos A, B e C estejam alinhados, o determinante de suas coordenadas deve ser igual a zero. Assim, temos que:

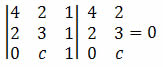
Fazendo o cálculo do determinante obtemos:
12 + 0 + 2c – 4 – 4c – 0 = 0
ou
8 – 2c = 0
2c = 8
c = 4.

Exemplo 3. Para quais valores reais de k os pontos (6, k), (3, 4) e (2 – k, 2) são colineares?
Solução: dizer que os pontos são colineares é o mesmo que dizer que eles estão alinhados. Dessa forma, devemos fazer o cálculo do determinante e igualá-lo a zero.


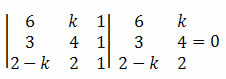
Desenvolvendo o determinante, obtemos:
– k² + 3k + 10 = 0
ou
k² – 3k – 10 = 0
Resolvendo a equação acima, obtemos:
k = 5 ou k = – 2