Equação da hipérbole

No estudo da geometria analítica, as diversas figuras geométricas são estudadas do ponto de vista algébrico. Ponto, retas, circunferências são esquematizadas com o auxílio da álgebra. As cônicas, que são figuras geométricas oriundas de secções transversais realizadas em um cone, também são muito exploradas. A própria circunferência, a elipse, a parábola e a hipérbole são classificadas de cônicas. Vejamos como a hipérbole pode ser explorada do ponto de vista da geometria analítica.

Definição de hipérbole: Considere F₁ e F₂ como sendo dois pontos distintos do plano e 2c a distância entre eles. Hipérbole é o conjunto dos pontos do plano, tais que a diferença, em valor absoluto, das distâncias à F₁ e F₂ é a constante 2a (0 < 2a < 2c).
A hipérbole pode ter os focos sobre o eixo x ou sobre o eixo y e sua equação varia em cada um dos casos. Vamos deduzir sua equação para cada um dos casos citados.

Hipérbole com focos sobre o eixo x.

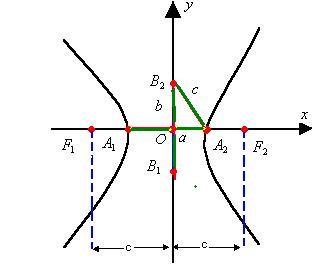
Como os focos da hipérbole estão localizados sobre o eixo x, suas coordenadas serão: F₂(c, 0) e F₁(– c, 0). Nesse caso, a equação da hipérbole será do tipo:

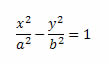
Hipérbole com focos sobre o eixo y.

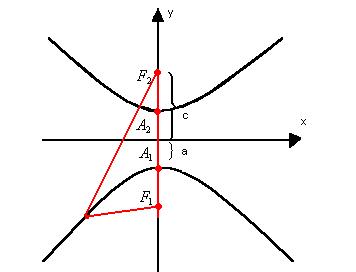
Como os focos da hipérbole estão sobre o eixo y, suas coordenadas serão: F₂(0, c) e F₁(0, – c). Nesse caso, a equação da hipérbole será do tipo:

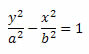
Elementos e propriedades da hipérbole:
2c → é a distância focal.
c² = a² + b² → relação fundamental.
A₁(– a, 0) e A₂(a, 0) → são os vértices da hipérbole.
2a → é a medida do eixo real.
2b → é a medida do eixo imaginário.
c/a → é a excentricidade

Exemplo 1. Determine a equação da hipérbole com focos F₁(– 10, 0) e F₂(10, 0) e eixo real medindo 16 unidades.
Solução: De acordo com as coordenadas dos focos percebemos que eles estão sobre o eixo x, pois as coordenadas y são iguais a zero. Também podemos afirmar que c = 10.

Foi dado que o eixo real tem 16 unidades de comprimento. Logo, temos que:
2a = 16 → a = 8

Para determinar a equação da hipérbole precisamos conhecer os valores de a e b, portanto devemos utilizar a relação fundamental para encontrarmos o valor de b. Segue que:
c² = a² + b²
10² = 8² + b²
b² = 100 – 64
b² = 36
b = 6

Conhecidos os valores de a e b podemos escrever a equação da hipérbole com focos sobre o eixo x:


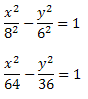
Exemplo 2. Determine as coordenadas dos focos da hipérbole de equação:

Solução: Observando a equação da hipérbole podemos constatar que seus focos estão sobre o eixo y, logo terão coordenadas do tipo F₁(0, – c) e F₂(0, c).
Da equação da hipérbole obtemos que:
a² = 16 → a = 4
b² = 9 → b = 3
Utilizando a relação fundamental, teremos:
c² = a² + b²
c² = 16 + 9
c² = 25
c = 5
Portanto, os focos da hipérbole são F₁(0 , – 5) e F₂(0, 5).
Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática