Entende-se por elipse o lugar geométrico de um plano onde a soma da distância de sua extremidade a dois pontos fixos, chamados de focos, F1 e F2, resulta em uma constante 2a, onde 2a > 2c.
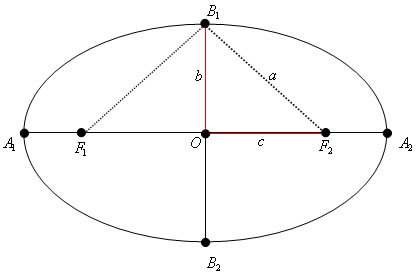
Na ilustração da elipse acima temos:
F1 e F2 são os focos da elipse e a distância entre eles é a distância focal (2c).
O segmento A1A2 é o maior eixo da elipse e sua medida é a soma da definição 2a.
O segmento B1B2 é o menor eixo da elipse e sua medida corresponde a 2b.
O centro O é o ponto médio entre os eixos da elipse e os focos A1A2 e F1F2.
A excentricidade da elipse é calculada pela razão entre c e a.
Na elipse, a relação de Pitágoras é válida entre as medidas de a, b e c. Dessa forma, temos que:
a² = b² + c²
Equação reduzida da elipse
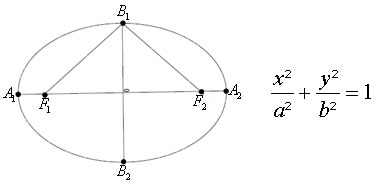
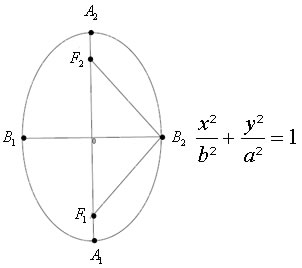
De acordo com a posição dos focos em relação aos eixos das abscissas e das ordenadas, a elipse possui as seguintes equações reduzidas:
F1 e F2 são os focos da elipse e a distância entre eles é a distância focal (2c).
O segmento A1A2 é o maior eixo da elipse e sua medida é a soma da definição 2a.
O segmento B1B2 é o menor eixo da elipse e sua medida corresponde a 2b.
O centro O é o ponto médio entre os eixos da elipse e os focos A1A2 e F1F2.
A excentricidade da elipse é calculada pela razão entre c e a.
Na elipse, a relação de Pitágoras é válida entre as medidas de a, b e c. Dessa forma, temos que:
a² = b² + c²
Equação reduzida da elipse
De acordo com a posição dos focos em relação aos eixos das abscissas e das ordenadas, a elipse possui as seguintes equações reduzidas:
Exemplo 1
Vamos determinar as equações das seguintes elipses:
a)
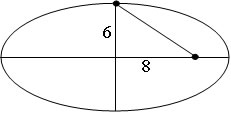
Vamos determinar as equações das seguintes elipses:
a)

a² = b² + c²
a² = 6² + 8²
a² = 36 + 64
a² = 100
a = 10
Equação:
a² = 6² + 8²
a² = 36 + 64
a² = 100
a = 10
Equação:
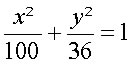
b)
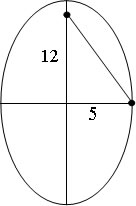
a² = b² + c²
a² = 5² + 12²
a² = 25 + 144
a² = 169
a = 13
Equação:
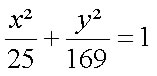
Exemplo 2
Vamos determinar os focos e as extremidades do eixo maior da elipse de equação 9x² + 36y² = 144.
Temos que 16 > 4, portanto, o eixo maior está na abscissa (x). Dessa forma:
a² = 16 → a = 4
b² = 4 → a = 2
a² = b² + c² → 16 = 2 + c² → c² = 16 – 2 → c² = 14
Os focos são F1(14,0) e F2(–14,0) e as extremidades dos eixos maiores são A1(5,0) e A2(–5,0).
A elipse possui uma importante aplicação na Astronomia, pois os planetas descrevem movimentos elípticos em órbita do sol, estando localizados nos focos da elipse. Essa teoria foi descoberta e comprovada por Johannes Kepler (1571 – 1630), grande astrônomo alemão.
a² = 16 → a = 4
b² = 4 → a = 2
a² = b² + c² → 16 = 2 + c² → c² = 16 – 2 → c² = 14
Os focos são F1(14,0) e F2(–14,0) e as extremidades dos eixos maiores são A1(5,0) e A2(–5,0).
A elipse possui uma importante aplicação na Astronomia, pois os planetas descrevem movimentos elípticos em órbita do sol, estando localizados nos focos da elipse. Essa teoria foi descoberta e comprovada por Johannes Kepler (1571 – 1630), grande astrônomo alemão.
www.mundoeducacao.com.br
os focos F1(0,4) e F2 (0,- 4) e as extremidades do eixo maior A1(0,6) e A2(0,-6) ;
ResponderExcluir