Diagonais de um polígono convexo

Marcelo Rigonatto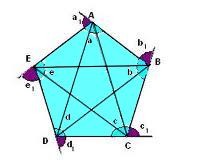

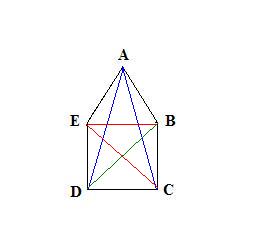
Pentágono

Os polígonos são formas geométricas planas formadas por segmentos de reta que formam uma região fechada. Essas figuras são classificadas de acordo com o número de lados e possuem características e propriedades que variam de um para outro. O polígono com menor número de lados é o triângulo. É através do número de lados que podemos determinar quantas diagonais o polígono possui. Diagonal é o segmento de reta que une dois vértices não consecutivos de um polígono.

Vejamos o exemplo do quadrado:

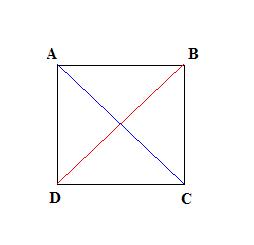
O quadrado possui duas diagonais: AC e BD.

Existe uma fórmula que determina quantas diagonais há num polígono de n lados.

Onde,
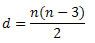
D → é o número de diagonais do polígono.
n → é o número de lados do polígono.

Exemplo 1. Determine o número de diagonais do polígono abaixo.

Solução: O polígono tem 5 lados (pentágono), assim, utilizando a fórmula teremos:

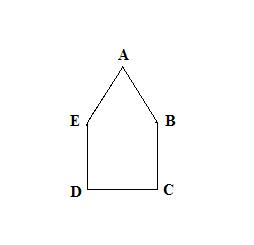
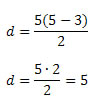
Portanto, o pentágono possui 5 diagonais.

Exemplo 2. Quantas diagonais possui o decágono?

Solução: Decágono é um polígono com 10 lados. Assim, teremos:

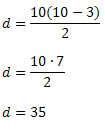
Portanto, o decágono possui 35 diagonais.

Exemplo 3. Determine quantos lados possui um polígono com 90 diagonais.

Solução: Sabemos que o número de diagonais é 90 e precisamos determinar o número de lados desse polígono. Utilizaremos a fórmula do número de diagonais para descobrir a quantidade de lados do polígono.


Portanto, o polígono que apresenta 90 diagonais tem 15 lados.

Exemplo 4. Qual o polígono que não apresenta diagonais?

Solução: o único polígono que não possui diagonais é o triângulo, uma vez que seus vértices são consecutivos. Através da fórmula acima também podemos verificar essa propriedade. Veja:

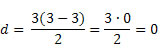
Exemplo 5. Quantas diagonais possui um polígono com 22 lados?

Solução: Temos que n = 22 lados. Assim,


Portanto, um polígono com 22 lados apresenta 209 diagonais.