Equações Biquadradas

Danielle de Miranda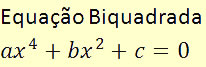

Equação de 4º grau

Equação biquadrada é uma equação de quarto grau, que para achar os valores de suas raízes é preciso transformá-la em uma equação de 2º grau.
Essa equação é escrita da seguinte forma geral: ax⁴ + bx² + c = 0.

Onde a ≠ 0 e b e c devem assumir valores reais.

Para resolver (encontrarmos as sua raízes) é preciso transformá-las em uma equação do segundo grau. Isso ocorre através de uma transformação e substituição de incógnitas.

Para melhor compreensão, veja no exemplo abaixo como essa transformação acontece e como chegamos às raízes da equação biquadrada.

4x⁴ – 17x² + 4 = 0 → equação biquadrada

4(x²)² – 17x² + 4 = 0 → também pode ser escrita assim.

Substituindo variáveis: x² = y, isso significa que onde for x² iremos colocar y.

4y² – 17y + 4 = 0 → agora resolvemos essa equação do 2º grau encontrando x’ e x”.

a = 4 b = -17 c = 4

∆ = b² – 4ac
∆ = (-17)² – 4 . 4 . 4
∆ = 289 - 64
∆ = 225

x = - b ± √∆
2a

x = -(-17) ± √225
2 . 4

x = 17 ± 15
8

x’ = 17 + 15 = 32 : 8 = 4
8

x” = 17 – 15 = 2 = 1
8 8 4

Essas são as raízes da equação 4y² – 17y + 4 = 0, para encontrarmos as raízes da equação biquadrada
4x⁴ – 17x² + 4 = 0 devemos substituir os valores de x’ e x” em
x² = y.

Para x = 4
x² = y
x² = 4
x = √4
x = ± 2

Para x = 1
4
x² = y
x² = 1
4

y = ±1
2

Portanto, a solução da equação biquadrada será:

S = {-2, -1, 1, 2}.
2 2