Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Para entendermos como agir em situações que envolvem probabilidade na união de dois eventos, precisamos falar sobre espaço amostral e eventos.
Espaço amostral: consiste em todos os resultados provenientes de um determinado experimento aleatório.
Evento: está relacionado ao espaço amostral, pois consiste no subconjunto do espaço amostral.
Situação no lançamento de um dado
Lançamento de um dado:
Espaço amostral: (1, 2, 3, 4, 5, 6)
Eventos: (1), (2), (3), (4), (5), (6)
Podemos ter no lançamento de um dado a probabilidade envolvendo a união de dois eventos, antes vamos definir algumas situações da ocorrência da união de dois eventos.
Condições:
Para que ocorra a união de dois eventos devemos ter o mesmo espaço amostral. Vamos considerar duas situações possíveis da união de A com B (A U B).
A ∩ B = Ø
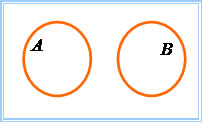
Se a intersecção entre os conjuntos A e B formam um conjunto vazio, isto é, os conjuntos não possuem termos em comum, podemos definir que A U B = A+B, considerando que o espaço amostral seja diferente de zero chegamos à seguinte conclusão:
p(A U B) = p(A) + p(B)
A ∩ B ≠ Ø
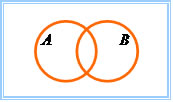
Se a intersecção entre os conjuntos A e B formam um conjunto não vazio, indica que eles possuem elementos em comum, dessa forma a probabilidade da união desses dois eventos pode ser definida da seguinte forma A U B = A+B – (A ∩ B), então:
p(A U B) = p(A) + p(B) – p(A ∩ B)
Exemplo
No lançamento de um dado, qual a probabilidade de o número obtido ser múltiplo de 2 ou de 3?
Múltiplos de 2: A = {2, 4, 6}
Múltiplos de 3: B = {3, 6}
Podemos notar que A∩B≠Ø, então: p(A U B) = p(A) + p(B) – p(A ∩ B)p(A) = 3/6
p(B) = 2/6
p(A) ∩ p(B) = 1/6
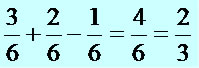
www.mundoeducacao.com.br
Nenhum comentário:
Postar um comentário