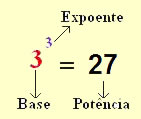
Potenciação: Definição e Exemplos

Potência

Podemos dizer que potenciação representa uma multiplicação de fatores iguais, se temos a seguinte multiplicação: 2 x 2 x 2 x 2 x 2 x 2, podemos representá-la usando a potência 2⁶, onde 2 é a base e 6 o expoente (Leia: dois elevado a sexta potência).

O expoente possui um papel fundamental na potenciação, pois ele é quem define quantas vezes a base será multiplicada por ela mesma. Observe:

2⁶ = 2 x 2 x 2 x 2 x 2 x 2 = 64
4² = 4 x 4 = 16
5³ = 5 x 5 x 5 = 125
10² = 10 x 10 = 100
12² = 12 x 12 = 144
3⁵ = 3 x 3 x 3 x 3 x 3 = 243
6³ = 6 x 6 x 6 = 216

Casos de potenciação

Todo número diferente de zero e elevado a zero é um.
2⁰ = 1
3⁰ = 1
10⁰ = 1
4⁰ = 1
125⁰ = 1

Todo número diferente de zero e elevado a um é o próprio número.
2¹ = 2
3¹ = 3
15¹ = 15
20¹ = 20
12¹ = 12

Base zero e qualquer número no expoente, o resultado será zero.
0⁵ = 0
0¹² = 0
0¹⁰⁰ = 0
0⁷ = 0
0²⁵ = 0

Base negativa e expoente ímpar, resultado negativo.
(-3)³ = (-3) x (-3) x (-3) = -27
(-4)⁵ = (-4) x (-4) x (-4) x (-4) x (-4) = -1024
(-2)⁷ = (-2) x (-2) x (-2) x (-2) x (-2) x (-2) x (-2) = -128

Base negativa e expoente par, resultado positivo.
(-2)⁴ = (-2) x (-2) x (-2) x (-2) = + 16
(-6)² = (-6) x (-6) = + 36
(-7)² = (-7) x (-7) = + 49

Base é um número racional (fração): devemos elevar ao expoente indicado o numerador e o denominador da fração.



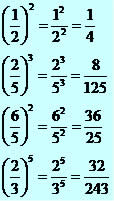
Quando o expoente é um número negativo: invertemos a base e mudamos o sinal do expoente para positivo.




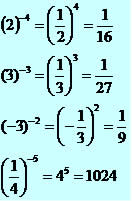
Uma importante aplicação de potenciação é a notação científica, usada para expressar valores muito grandes ou muito pequenos. A notação é usada por cientistas, como astrônomos, físicos, biólogos, químicos entre outros.

Exemplos:
6 120 000, podemos representá-lo usando a seguinte notação decimal 6,12 * 10⁶

0,00012, pode ser representado por 1,2 * 10^-4.

Marcos Noé