O Sonho, O Discurso, O Método e A Razão
DESCARTES ( 1596-1650) LA HAYE; PARIS, LEIDEN, ESTOCOLMO
 | É considerado o filósofo que, individualmente, mais contribuiu para o progresso das ciências exatas. Advogado e filho de advogado, nasceu em La Haye, na França, a 31 de março de 1596. Estudou numa escola jesuítica e, em 1616, formou-se em direito na Universidade de Poitiers. Insatisfeito com a formação escolástica que recebera, rompeu com a filosofia aristotélica adotada nas academias, propôs uma nova concepção do Universo, formulou a geometria analítica e criou as bases do método científico moderno. No início da Guerra do Trinta Anos integrou-se às tropas do príncipe Maurício de Nassau, o mesmo que, em 1637, vem a Pernambuco, governar a região dominada pelos holandeses. Como militar, Descartes não participou de batalhas e dedicou-se integralmente à matemática. Começou a formular sua geometria analítica e seu “método de raciocinar corretamente” com apenas 22 anos. Ao procurar a premissa mais elementar e irrefutável que servisse de base para construir seu método de raciocínio, formulou o axioma “penso, logo existo”, base de todo o racionalismo científico. |
Soldado, intelectual e cavalheiro, René Descartes fundamentou sua teoria na dúvida. Nunca teve um professor de matemática e teve poucos alunos. Uma aluna, a princesa Cristina da Suécia, para onde se mudou em 1649, fazia com que ele se levantasse às 5 horas da manhã, nos dias gelados de inverno. Talvez por isso não resistiu e morreu de pneumonia, a 11 de fevereiro de 1650.
As realizações supremas de Descartes são sua filosofia e a geometria analítica (esta última partilhada com Fermat). Entre suas contribuições à álgebra estão o aperfeiçoamento da notação, o método dos coeficientes indeterminados e a regra de sinais. Introduziu o conceito de eixo instantâneo na análise que fez da ciclóide. E antecipou-se a Euler no teorema sobre poliedros.
As realizações supremas de Descartes são sua filosofia e a geometria analítica (esta última partilhada com Fermat). Entre suas contribuições à álgebra estão o aperfeiçoamento da notação, o método dos coeficientes indeterminados e a regra de sinais. Introduziu o conceito de eixo instantâneo na análise que fez da ciclóide. E antecipou-se a Euler no teorema sobre poliedros.
(Texto extraído do quadro "Men of Modern Mathematics". Tradução de Higyno H. Domingues).
ALGUMAS CURIOSIDADES SOBRE RENE DESCARTES
(Texto: Prof. Hermes Antonio Pedroso - Pesquisador sobre História da Matemática do Departamento de Matemática do IBILCE/UNESP)
(Texto: Prof. Hermes Antonio Pedroso - Pesquisador sobre História da Matemática do Departamento de Matemática do IBILCE/UNESP)
 Nascimento: 31 de março de 1596 em La Haye, hoje Descartes (França), pequena cidade a sudoeste e a 300 km de Paris, província de Touraine. Pais: Nikolaj e Bárbara Watzelrode. O pai era um próspero comerciante de cobre, assim como seus antepassados.Com a morte do pai em 1483 foi viver juntamente com a mãe e os irmãos (Andreas, Bárbara e Catarina) na residência do tio materno Lucas Watzelrode, cônego de Wloclawek. O século XVII: Marca o início da Ciência Moderna e é a última fase da transição geral da economia feudal para a capitalista. A ascensão da burguesia tem tudo a ver com o nascimento dessa nova Ciência. Afinal de contas a ciência permite dominar a natureza: navios melhores, armas mais eficazes, máquinas e mecanismos mais produtivos, produtos aprimorados. Em suma, lucros e lucros. |  |
Situação Política: A época em que viveu Descartes foi marcada por conflitos políticos em toda Europa. O mais importante foi sem dúvida a Guerra dos Trinta Anos, que de 1618 a 1648 devastou a Alemanha e impôs grandes perdas humanas e materiais à França, Espanha, Holanda, Dinamarca e Suécia.Entre as causas dessa longa guerra está a diferença religiosa que então opunha Católicos e Protestantes, e no caso todos tinham interesses políticos.
 | Ensino Fundamental: Matriculou-se aos 8 anos no Colégio jesuíta de La Flèche, na época considerado o melhor da Europa. Lá eram ministrados dois tipos de conhecimentos: as ciências "práticas”, úteis a um oficial (Matemática, Geografia, noções de máquinas e fortificações, Hidrografia, etc.); e as “letras”, ou conhecimentos humanísticos (Gramática, História, Poesia, Retórica, Filosofia e Moral).Aluno Especial: Como sempre teve saúde frágil não lhe era cobrada no colégio a regularidade da freqüência às aulas e foi nessa época que adquiriu o hábito de permanecer na cama de manhã, para leituras e meditações. Às vezes chegava a sonhar e tomava decisões a partir dos sonhos. Anos mais tarde, diria que seus melhores pensamentosfilosóficos matemáticos surgiram pela manhã, deitado e em estado de meditação. |
O diretor do colégio registrou no livro de matrícula: “Este menino é pálido, magro e sua estatura é muito baixa para sua idade. Tem os pulmões fracos e uma tosse crônica. Por estes traços, será necessário que, antes de instruirmos sua mente, cuidemos de seu corpo. Ele não deverá deixar o seu leito, ao acordar, se não sentir-se bem disposto.”
Ao concluir seu curso em La Flèche, Descartes formulou questões básicas para o futuro:
- Há algum ramo do conhecimento que realmente ofereça segurança?
- Como nós sabemos alguma coisa?
- O que é o conhecimento?
- Existiriam leis para a moral?
- Penso: existo? Ou penso, logo existo?
 | Ensino Superior: Aos 20 anos de idade graduou-se em Direito pela Universidade de Poitiers e estabeleceu-se em Paris a fim de iniciar-se na vida mundana, como convinha a alguém da sua posição. Mas reencontrou-se com Marin Mersene (1588-1648) que conhecera em La Flèche e por dois anos dedicaram-se à Matemática com todas as suas forças. Os sonhos decisivos: Na noite de 10 de novembro de 1619 depois de beber muito numa festa, Descartes teve forte e tenebroso pesadelo, constituído de três sonhos esquisitos. Num deles viu-se recitando um poema que revelava o caminho que deveria seguir, ou seja, usar o método matemático como modelo para a aquisição de conhecimento. O Discurso do Método: Em 1637 publicou na Holanda, em francês, seu grandioso “Discours de la Méthode pour bien conduire la Raison e chercher la Vérité dans les Sciences” (Discurso sobre o Método para bem conduzir a Razão e procurar a Verdade nas Ciências). |
| “O bom senso é a coisa do mundo mais bem distribuída, porque cada qual pensa ser tão bem provido dele que mesmo os mais difíceis de contentar noutras coisas não costumam desejar mais do que o que têm. E não é verossímil que todos se enganem a tal respeito; antes isso mostra que o poder de bem julgar e distinguir o verdadeiro do falso, que é propriamente que se chama bom senso ou razão, é naturalmente igual em todos os homens; e que assim a diversidade das opiniões não resulta de serem uns mais racionais do que os outros, mas somente de que conduzimos os nossos pensamentos por caminhos diversos e não consideramos as mesmas coisas”. |  |
 | O Conteúdo pode ser dividido em seis partes:
|
As quatro regras:- Clareza e distinção: só devo acolher como verdadeiro o que se apresente ao meu espírito de forma tão clara e distinta que eu não tenha como duvidar;
- Análise: em presença de dificuldades no conhecimento, devo dividi-las em tantas parcelas quantas forem necessárias para chegar a partes claras e distintas e, assim, solucionar o problema;
- Ordem: devo conduzir meus pensamentos por ordem, começando pelos mais simples e prosseguindo na direção dos mais complexos ou compostos;
- Enumeração: proceder a revisões e enumerações completas, para ter a certeza de que todos os elementos foram considerados, ou seja, verificar o resultado final.
Os três apêndices:
Teorema: Deus existe.
Prova: para Descartes a idéia de Deus é uma idéia perfeita. Ora, o ser humano sendo imperfeito, não tem idéias perfeitas. Se o homem é um ser imperfeito e tem uma idéia perfeita, que é a idéia de Deus, esta idéia só pode existir no homem dada a ele por Deus. Então, Deus existe.
|  |
Outras obras: - Regras para direção do espírito;
- Meditações metafísicas;
- Princípios de filosofia;
- O tratado das paixões da alma.
- Importante: Para Descartes todos os fenômenos naturais são causados por simples movimentos internos da matéria que compõe os corpos, tudo é extensão e movimento, o resto é aparência. A primeira coisa a fazer, portanto, é estudar o movimento.
Vida Pessoal: Sua mãe faleceu poucas semanas após o seu nascimento, sendo criado pela avó materna e uma tia. Nunca se casou, porém teve um caso amoroso com uma empregada doméstica de treze anos, Helena, com a qual teve uma filha, Francine. Quando estava tudo preparado para o casamento, sua filha morreu, vítima de grave doença. Desgostoso, jamais se casou e sempre dizia: “Eu aprecio a beleza das mulheres, mas gosto muito mais de suas verdades”. Inimigos, teve alguns sendo Fermat, Étienne Pascal e Roberval os mais famosos. O único amigo, sem dúvida, foi o padre Marin Mersenne. | O fim na Suécia: depois de vinte anos vivendo na Holanda, Descartes foi convidado pela jovem rainha Cristina da Suécia para fazer parte de sua Corte. A rainha decidiu tomar lições de matemática e filosofia, às cinco horas das manhãs gélidas de Estocolmo. Devido a sua saúde sempre muito frágil, não resistiu ao frio excessivo, vindo a falecer de pneumonia, em 11 de fevereiro de 1650, aos 54 anos de idade. A rainha ordenou que lhe decepassem a cabeça, para conservá-la no mel. O corpo foi enviado à França, onde o enterraram. A cabeça de Descartes só voltou à sua terra natal em março de 1809, quando os suecos homenagearam o filósofo. |
Homenagens:- O matemático holandês Frans van Schooten (1615-1660) publicou uma versão para o latim de La Géométrie, de Descartes em 1649. Posteriormente em novas edições, acrescentou comentários importantes. Assim, pode-se dizer, que Descartes introduziu a geometria analítica e Schooten a tornou conhecida.
- Sistema Cartesiano: foi Leibniz (1646-1716) o primeiro a usar o termo cartesiano de Cartesius (Descartes em Latim).
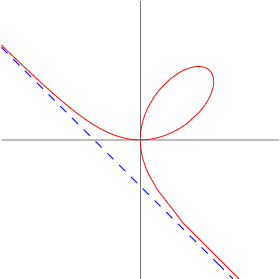
- Folium de Descartes: uma cúbica estudada pelos Bernoullis que diziam ser de Descartes.
Banner do projeto: 
REFERÊNCIAS BIBLIOGRÁFICAS:BOYER, C. B. História da matemática. 2.ed. São Paulo: Edgard Blücher, 1996. 510p. EVES, H. Introdução à história da matemática. Campinas: Editora da Unicamp, 1995. 843p. .
PEDROSO, H. A. História da matemática. São José do Rio Preto: Gráfica da UNESP, 1992. 220p.
REY PASTOR, J.; BABINI, J. História de la matemática. Buenos Aires: Espasa- calpe Argentina, 1951. 388p.
STRUIK, D. J. História concisa das matemáticas. 3.ed. Lisboa: Gradiva, 1997. 395p.
TATON, R. História geral das ciências – A ciência contemporânea. São Paulo: Difusão Européia do Livro, 1966.
Galeria de Imagens:
fonte http://www.ibilce.unesp.br/
Nenhum comentário:
Postar um comentário