Formula com 3 Conjuntos

4) Sabendo que a fórmula do número de elementos da união de dois conjuntos é n(A U B) = n(A) + n(B) - n(A ∩ B), determine a fórmula da união de 3 conjuntos n(A U B U C). 

Resolução:

Muito interessante essa pergunta. Geralmente usamos as fórmulas, mas infelizmente as pessoas não estão muito interessadas em saber de onde vieram as fórmulas. A melhor coisa é você saber de onde veio a fórmula porque aí não tem como você esquecer. Se esquecer da fórmula você deduz novamente.

Para chegar nessa fórmula vamos fazer uma figura. Nela fiz três conjuntos A, B e C se intersectando mutuamente.

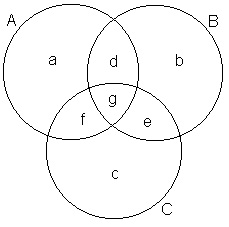
Veja que o total de elementos de A é igual à soma das seguintes regiões:

A = a + d + f + g

E da mesma forma os conjuntos B e C são a soma das seguintes regiões do desenho:

B = b + d + e + g

C = c + e + f + g

Então quando queremos saber a união dos 3 conjuntos temos que pegar a soma de todos os elementos de A com todos os elementos de B com todos os elementos de C. Mas se simplesmente somarmos todos os elementos de cada conjunto, estaremos pegando algumas regiões mais de uma vez. As regiões que são intersecção de apenas dois conjuntos (d, e, f) estaremos pegando duas vezes e a região da intersecção dos 3 conjuntos (g) estaremos somando 3 vezes. Então temos que subtrair algumas coisas.

Agora repare que os elementos da intersecção de cada dois conjuntos abrange duas regiões:

A ∩ B = d + g

A ∩ C = f + g

B ∩ C = e + g

Então quando procuramos n(A U B U C), se somarmos só n(A) + n(B) + n(C) estaremos somando duas vezes essas regiões de intersecção entre cada dois conjuntos, por isso na fórmula subtraímos cada uma delas:

- n(A ∩ B) - n(A ∩ C) - n(B ∩ C)

Mas ao subtrairmos cada uma delas, estamos subtraindo 3 vezes a região de intersecção entre os 3 conjuntos, que também tínhamos somado 3 vezes quando somamos o total de elementos de cada conjunto n(A) + n(B) + n(C), por isso na fórmula precisamos somar essa região de novo:

+ n(A ∩ B ∩ C)

Talvez você visualize melhor com as letras de cada região. Primeiro vou escrever cada parte da fórmula em função das letras de cada região:

n(A U B U C) = a + b + c + d + e + f + g

n(A) = a + d + f + g

n(B) = b + d + e + g

n(C) = c + e + f + g

n(A ∩ B) = d + g

n(A ∩ C) = f + g

n(B ∩ C) = e + g

n(A ∩ B ∩ C) = g

Agora colocando a fórmula toda:

= n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)

= (a+d+f+g) + (b+d+e+g) + (c+e+f+g) - (d+g) - (f+g) - (e+g) + (g)

= (a+b+2d+e+f+2g) + (c+e+f+g) - (d+g) - (f+g) - (e+g) + (g)

= (a+b+c+2d+2e+2f+3g) - (d+g) - (f+g) - (e+g) + (g)

= (a+b+c+d+2e+2f+2g) - (f+g) - (e+g) + (g)

= (a+b+c+d+2e+f+g) - (e+g) + (g)

= (a+b+c+d+e+f) + (g)

= (a+b+c+d+e+f+g)

= a + b + c + d + e + f + g

= n(A U B U C) 

Portanto a fórmula é:

n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)

http://www.cinoto.com.br/website/