Esse é o blog do Professor de Matemática Carlos Barroso. Trabalho no Colégio Estadual Dinah Gonçalves . Valéria-Salvador-Bahia .Inscreva-se Já no meu canal www.youtube.com/accbarroso1 e receba as videoaulas de Matemática.
sexta-feira, 16 de outubro de 2020
quinta-feira, 15 de outubro de 2020
quarta-feira, 14 de outubro de 2020
sexta-feira, 9 de outubro de 2020
quinta-feira, 8 de outubro de 2020
quarta-feira, 7 de outubro de 2020
segunda-feira, 3 de agosto de 2020
quinta-feira, 30 de julho de 2020
Compostos orgânicos Fórmulas estruturais e principais classes
Professor de Matemática e Biologia Antônio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
www.youtube.com/accbarroso1Os humanos têm usado os compostos orgânicos e suas reações por milhares de anos. Sua primeira experiência deliberada com uma reação orgânica data, provavelmente, da descoberta do fogo. Os egípcios antigos usavam os compostos orgânicos (índigo e alizarina) para tingir roupas. Tanto a fermentação de uvas, para produzir álcool etílico, quanto a qualidade ácida do "vinho azedo" são descritas na Bíblia.
O álcool faz parte de um rol de compostos orgânicos que já ultrapassa em muito a casa dos milhões e que é estudado por uma divisão da química responsável por analisar os compostos que apresentam o elemento carbono em sua composição: a Química Orgânica.
Os compostos de carbono são centrais para a vida em nosso planeta, incluindo-se desde o DNA - as moléculas helicoidais gigantes que contêm toda a informação genética (Figura 1) - até o metano, que contém um único átomo de carbono (Figura 2).


Figura 2: Estrutura do metano
Uma grande vantagem da teoria estrutural é que ela nos permite classificar o grande número de compostos orgânicos em um número relativamente pequeno de famílias, com base nas suas estruturas.
Grupo funcional
As moléculas de compostos orgânicos de uma família são caracterizadas pela presença de um determinado arranjo de átomos denominado grupo funcional.
Um grupo funcional é a parte da molécula onde as suas reações químicas ocorrem; é a parte que efetivamente determina as propriedades químicas do composto (e muitas das suas propriedades físicas também).
Os hidrocarbonetos - um grupo funcional bastante estudado no Ensino Médio - são compostos cujas moléculas contêm apenas átomos de carbono e hidrogênio. Vejamos alguns exemplos na tabela a seguir:

Vejamos também exemplos de estrutura de outros hidrocarbonetos:

O etano apresenta dois átomos de carbono e seis átomos de hidrogênios; o eteno, conhecido como etileno, é composto por dois átomos de carbono e quatro de hidrogênio; já o acetileno (ou etino) é composto por dois átomos de carbono e apenas dois átomos de hidrogênio; quanto ao benzeno, por seis átomos de carbono e de hidrogênio (Figura 3).

Subclassificação
Na família dos hidrocarbonetos também existe uma subclassificação, formada pelos alcanos (hidrocarbonetos formados por ligações simples: metano, etano e propano); pelos alcenos (hidrocarbonetos formados por ligações duplas carbono-carbono: eteno e propeno); e pelos alcinos (hidrocarbonetos formados por ligações triplas carbono-carbono, como, por exemplo, o etino e o propino).
Essas substâncias apresentam, além de outras funções orgânicas, regras específicas que justificam seus nomes. Mas essas regras não serão abordadas neste texto.
Conhecer a estrutura dos compostos orgânicos ajuda a identificar as substâncias orgânicas e as famílias (grupos funcionais) a que elas pertencem. Examine a tabela a seguir, que reúne vários dos grupos funcionais. Para simplificar o entendimento das funções na tabela, identifica-se apenas o grupo funcional, sendo "R" um substituinte alquila (radicais derivados de alcanos) ou arila (um radical orgânico derivado de um anel benzênico)

Observando as estruturas
A função orgânica álcool, citada no ínicio do texto, apresenta em sua estrutura uma ou mais hidroxilas ligadas a carbonos saturados (carbonos com ligações simples), ou seja, o grupo OH ligado a algum carbono. Veja o exemplo do 1-propanol na tabela.
O grupo carbonila - uma ligação dupla ligada ao oxigênio - é, provavelmente, o grupo funcional mais importante encontrado nas substâncias orgânicas. Substâncias que contêm o grupo carbonila são abundantes na natureza. Muitas desempenham um papel importante nos processos biológicos. Hormônios, vitaminas, aminoácidos, fármacos e flavonóides são apenas alguns exemplos de substâncias carboniladas que nos afetam diariamente.
Um grupo acila consiste em um grupo carbonila ligado a um grupo alquila ou arila:

Enfim, podemos identificar muitas das substâncias orgânicas com facilidade se observarmos como suas estruturas se apresentam. Essa identificação é importante para que possamos verificar o comportamento dos compostos orgânicos nas reações químicas - e até mesmo nomeá-los.
*Erivanildo Lopes da Silva e Marcus Vinicius Bahia são professores do curso de Química da Universidade Federal da Bahia (campus ICADS-Barreiras).
Transtornos alimentares Entenda o que são bulimia e anorexia

Colégio Estadual Dinah Gonçalves
email
accbarroso@hotmail.com
Karen Carpenter, vítima da bulimia
Os temas alimentação e transtornos alimentares nunca estiveram tão em alta quanto nos dias atuais. Nos jornais, na TV, na Internet, fala-se com freqüência sobre novos métodos e dietas milagrosas para emagrecer, sobre a necessidade de exercícios físicos e até sobre os riscos que os excessos na dieta e na ginástica podem provocar.
Teoricamente, toda essa discussão ocorre em nome da saúde e da obtenção e manutenção de um corpo belo, de acordo com os critérios da sociedade atual. Sim, porque, historicamente, o padrão de beleza mudou muito das volumosas mulheres do passado, até chegarmos às top models super-magras da atualidade.
No Renascimento, por exemplo, uma mulher linda deveria ter uma certa quantidade de gordura e formas arredondadas. Isso era uma garantia de que ela poderia gerar filhos saudáveis e ter condições de alimentá-los bem no primeiro ano de vida. Veja, por exemplo, como era rotunda a beleza das mulheres retratadas por da Vinci, Botticelli e Michelangelo.
Na verdade, ninguém deveria se preocupar em ir nem tanto ao mar, nem tanto à terra. Um ideal saudável de beleza talvez estivesse no equilíbrio entre estes dois extremos, havendo respeito às características genéticas de cada um e à sua estrutura física, com o consumo de uma dieta equilibrada conforme as atividades diárias exigem. Do mesmo modo, com a prática moderada de exercícios físicos, devidamente acompanhada por um especialista. Afinal, o objetivo é ter saúde e não desenvolver nenhum transtorno alimentar.
O que são transtornos alimentares?
Algumas pessoas desenvolvem desequilíbrios alimentares, como bulimia e anorexia, tornando-se assim extremamente magras. Estes transtornos não são novidades e um exemplo célebre disso ocorreu na década de 80, com a cantora Karen Carpenter, da banda The Carpenters (muito famosa nos anos 70). Karen vivia fazendo dieta. Isso perdurou muitos anos. Quando percebeu o problema e começou a se tratar, melhorou um pouco, mas logo morreu, em 1983. Devido à anorexia, a desnutrição afetou seu sistema cardíaco. Ela acabou sofrendo uma parada cardíaca.
Bulimia
Vamos examinar melhor as diferenças entre estes dois transtornos alimentares. Para começar, a bulimia. A origem dessa palavra é grega e compõe-se de bous (boi) e limos (fome). Referindo-se ao fato de os bois serem ruminantes, a palavra designa as pessoas que ingerem alimentos exageradamente e, depois, procuram eliminá-los por meio do uso de laxantes ou provocando o vômito.
O problema é que essa prática se torna rotineira, repetindo-se de duas a três vezes por semana. A partir daí, o indivíduo começa a ter tal controle sobre o momento de vomitar, que não precisa nem provocá-lo.
Bulimia, vômitos e subnutrição
As conseqüências fisiológicas do processo são graves: quando introduzimos um alimento em nossa boca, automaticamente o cérebro envia uma mensagem ao sistema digestório para que haja produção de sucos gástricos, a fim de facilitar a digestão. Em meio a essa atividade digestiva, ocorre o vômito. Com isso, os sucos digestivos podem afetar as paredes do esôfago, produzindo sangramentos junto com o vômito.
Outro risco é a subnutrição, pois o vômito constante altera a quantidade de vitaminas, proteínas, lipídios sais minerais, água e outros nutrientes absorvidos pelo organismo. Também podem apresentar problemas cardiovasculares, renais, endócrinos, dentários e sangramento da gengiva. Já o uso de laxantes pode implicar uma séria desidratação, pois há perda excessiva de água pelas fezes.
Verifica-se um maior número de bulímicos em algumas profissões, como ginastas, modelos profissionais, corredores de longa distância, dançarinos, já que existe uma exigência corporal muito grande em seu trabalho.
Anorexia nervosa
A anorexia nervosa consiste numa recusa em se alimentar. É, portanto, um transtorno caracterizado pela limitação da ingestão de alimentos, devido à obsessão com a magreza e o medo exagerado de ganhar peso. Note: apesar de estar magra, a pessoa continua se considerando acima do peso. Ela também não leva sua saúde em consideração, pois está mesmo é preocupada com o espelho.
Além de não comerem, as pessoas anoréxicas, normalmente praticam exercícios físicos em demasia. Também podem utilizar laxantes ou diuréticos e/ou provocarem o vômito, como os bulímicos.
Entre outros riscos da anorexia podemos apontar a interferência no ciclo menstrual, que pode ser desregulada ou interrompida; queda de cabelo; unhas quebradiças; desidratação; diminuição da pressão arterial e enfraquecimento muscular. Tudo isso decorre do fato de que, ao deixar de se alimentar, o organismo tenta suprir a falta de alimento realizando um processo denominado autofagia, ou seja, uma organela denominada lisossomo, libera enzimas que fazem a digestão das nossas próprias fibras musculares.
Anorexia e fatores emocionais
Convém lembrar que esse transtorno não se deve exclusivamente a problemas fisiológicos. Decorre também de causas emocionais, sócio-culturais, familiares, etc. Normalmente, a anorexia e a bulimia estão associados a uma faixa etária, a adolescência, podendo interferir no crescimento e desenvolvimento do paciente. Na maioria dos casos, ambos os transtornos atingem majoritariamente o sexo feminino.
O que deve ser feito quando se tem algum tipo de transtorno alimentar? Bem, normalmente o tratamento é baseado em duas frentes; na primeira cuida-se do quadro clínico (aspecto físico) e na segunda frente trata-se do aspecto emocional (psicológico) e para tais tratamentos são necessários profissionais especializados. Em alguns casos se faz necessária a internação, bem como o uso de antidepressivos.
* Cristina Faganelli Braun Seixas é bióloga e professora do Colégio Núcleo Educacional da Granja Viana.
sábado, 25 de julho de 2020
sexta-feira, 24 de julho de 2020
Expressão Numérica
Professor de Matemática Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
extraído do www.mundoeducacao.com.br
valor numérico de uma expressão numérica é preciso obedecer às regras de resolução de uma expressão numérica e quando encontramos em sua estrutura uma potência é preciso dar preferência a ela.
Veja alguns exemplos de expressões numéricas com potência em sua estrutura.
Exemplo:
• 3 . {43 – [5 . 60 + 7 . (92 – 80)]}
Nessa expressão numérica iremos resolver as potências 43, 60 e 92 antes de qualquer outra operação.
3 . {64 – [5 . 1 + 7 . (81 – 80)]}
Depois de eliminar todas as potências, é preciso aplicar as regas de resolução.
3 . {64 – [5 + 7 . 1 ]}
3 . {64 – [5 + 7]}
3 . {64 – 12}
3 . 52
156
• (33 + 3 . 7)2 : {4 . [800 – (32 . 2 + 10)2]}
Nessa expressão numérica iremos resolver as potências 33 e 32 antes de qualquer outra operação.
(27 + 3 . 7)2 : {4 . [800 – (9 . 2 + 10)2]}
Para resolvermos as potências (9 + 3 . 7)2 e (9 . 2 + 10)2 é preciso resolver as operações que estão dentro dos parênteses.
(27 + 21)2 : {4 . [800 – (18 + 10)2]}
2304 : {4 . [800 -784]}
2304 : {4 . 16}
2304 : 64
36
NOÇÕES DE LÓGICA MATEMÁTICA
CÁLCULO PROPOSICIONAL
Como primeira e indispensável parte da Lógica Matemática temos o CÁLCULO PROPOSICIONAL ou CÁLCULO SENTENCIAL ou ainda CÁLCULO DAS SENTENÇAS.
CONCEITO DE PROPOSIÇÃO
PROPOSIÇÃO: sentenças declarativas afirmativas (expressão de uma linguagem) da qual tenha sentido afirmar que seja verdadeira ou que seja falsa.
· A lua é quadrada.
· A neve é branca.
· Matemática é uma ciência.
Não serão objeto de estudo as sentenças interrogativas ou exclamativas.
OS SÍMBOLOS DA LINGUAGEM DO CÁLCULO PROPOSICIONAL
· VARIÁVEIS PROPOSICIONAIS: letras latinas minúsculas p,q,r,s,.... para indicar as proposições (fórmulas atômicas) .
Exemplos: A lua é quadrada : p
A neve é branca : q
· CONECTIVOS LÓGICOS: As fórmulas atômicas podem ser combinadas entre si e, para representar tais combinações usaremos os conectivos lógicos :
Ù: e , Ú: ou , ® : se...então , « : se e somente se , ~: não
· A lua é quadrada e a neve é branca. : p Ù q (p e q são chamados conjunctos)· A lua é quadrada ou a neve é branca. : p Ú q ( p e q são chamados disjunctos)
· Se a lua é quadrada então a neve é branca. : p ® q ( p é o antecedente e q o conseqüente)
· A lua é quadrada se e somente se a neve é branca. : p « q
· A lua não é quadrada. : ~p
Exemplos:
· Se a lua é quadrada e a neve é branca então a lua não é quadrada. :
((p Ù q) ® ~ p)· A lua não é quadrada se e somente se a neve é branca. :
((~ p) «q))
1. Toda fórmula atômicaé uma fórmula.
2. Se A e B são fórmulas então
(A Ú B) , (A Ù B) , (A ® B) , (A « B) e (~ A) também são fórmulas.
3. São fórmulas apenas as obtidas por 1. e 2. .
Com o mesmo conectivo adotaremos a convenção pela direita.
Exemplo: a fórmula p Ú q Ù ~ r ® p ® ~ q deve ser entendida como
(((p Ú q) Ù (~ r)) ® ( p ® (~ q)))
AS TABELAS VERDADE
A lógica clássica é governada por três princípios (entre outros) que podem ser formulados como segue:
· Princípio da Identidade: Todo objeto é idêntico a si mesmo.
· Princípio da Contradição: Dadas duas proposições contraditórias (uma é negação da outra), uma delas é falsa.
· Princípio do Terceiro Excluído: Dadas duas proposições contraditórias, uma delas é verdadeira.
Com base nesses princípios as proposições simples são ou verdadeiras ou falsas - sendo mutuamente exclusivos os dois casos; daí dizer que a lógica clássica é bivalente.
Para determinar o valor (verdade ou falsidade) das proposições compostas (moleculares), conhecidos os valores das proposições simples (atômicas) que as compõem usaremos tabelas-verdade :
1.Tabela verdade da "negação" : ~p é verdadeira (falsa) se e somente se p é falsa (verdadeira).
2. Tabela verdade da "conjunção" : a conjunção é verdadeira se e somente os conjunctos são verdadeiros.
3. Tabela verdade da "disjunção" : a disjunção é falsa se, e somente, os disjunctos são falsos.
4. Tabela verdade da "implicação": a implicação é falsa se, e somente se, o antecedente é verdadeiro e o conseqüente é falso.
5. Tabela verdade da "bi-implicação": a bi-implicação é verdadeira se, e somente se seus componentes são ou ambos verdadeiros ou ambos falsos
Exemplo: Construir a tabela verdade da fórmula : ((p Ú q) ® ~p) ® (q Ù p)
·NÚMERO DE LINHAS DE UMA TABELA-VERDADE: Cada proposição simples (atômica) tem dois valores V ou F, que se excluem. Para n atômicas distintas, há tantas possibilidades quantos são os arranjos com repetição de 2 (V e F) elementos n a n. Segue-se que o número de linhas da tabela verdade é 2n. Assim, para duas proposições são 22 = 4 linhas; para 3 proposições são 23 = 8; etc.
Exemplo: a tabela - verdade da fórmula ((p Ù q) ® r) terá 8 linhas como segue :
NOTA: "OU EXCLUSIVO" É importante observar que "ou" pode ter dois sentidos na linguagem habitual: inclusivo(disjunção) Ú ("vel") e exclusivo Ú ( "aut") onde p Úq significa ((p Ú q) Ù~ (p Ù q)).
Como primeira e indispensável parte da Lógica Matemática temos o CÁLCULO PROPOSICIONAL ou CÁLCULO SENTENCIAL ou ainda CÁLCULO DAS SENTENÇAS.
CONCEITO DE PROPOSIÇÃO
PROPOSIÇÃO: sentenças declarativas afirmativas (expressão de uma linguagem) da qual tenha sentido afirmar que seja verdadeira ou que seja falsa.
· A lua é quadrada.
· A neve é branca.
· Matemática é uma ciência.
Não serão objeto de estudo as sentenças interrogativas ou exclamativas.
OS SÍMBOLOS DA LINGUAGEM DO CÁLCULO PROPOSICIONAL
· VARIÁVEIS PROPOSICIONAIS: letras latinas minúsculas p,q,r,s,.... para indicar as proposições (fórmulas atômicas) .
Exemplos: A lua é quadrada : p
A neve é branca : q
· CONECTIVOS LÓGICOS: As fórmulas atômicas podem ser combinadas entre si e, para representar tais combinações usaremos os conectivos lógicos :
· Se a lua é quadrada então a neve é branca. : p ® q ( p é o antecedente e q o conseqüente)
· A lua é quadrada se e somente se a neve é branca. : p « q
· A lua não é quadrada. : ~p
Exemplos:
((p Ù q) ® ~ p)· A lua não é quadrada se e somente se a neve é branca. :
((~ p) «q))
2. Se A e B são fórmulas então
(A Ú B) , (A Ù B) , (A ® B) , (A « B) e (~ A) também são fórmulas.
3. São fórmulas apenas as obtidas por 1. e 2. .
Com o mesmo conectivo adotaremos a convenção pela direita.
Exemplo: a fórmula p Ú q Ù ~ r ® p ® ~ q deve ser entendida como
(((p Ú q) Ù (~ r)) ® ( p ® (~ q)))
AS TABELAS VERDADE
A lógica clássica é governada por três princípios (entre outros) que podem ser formulados como segue:
· Princípio da Identidade: Todo objeto é idêntico a si mesmo.
· Princípio da Contradição: Dadas duas proposições contraditórias (uma é negação da outra), uma delas é falsa.
· Princípio do Terceiro Excluído: Dadas duas proposições contraditórias, uma delas é verdadeira.
Com base nesses princípios as proposições simples são ou verdadeiras ou falsas - sendo mutuamente exclusivos os dois casos; daí dizer que a lógica clássica é bivalente.
Para determinar o valor (verdade ou falsidade) das proposições compostas (moleculares), conhecidos os valores das proposições simples (atômicas) que as compõem usaremos tabelas-verdade :
1.Tabela verdade da "negação" : ~p é verdadeira (falsa) se e somente se p é falsa (verdadeira).
| p | ~p |
| V | F |
| F | V |
| p | ||||||
V
|
F
| V | ||||
V
|
F
| F | ||||
V
|
V
| F | ||||
F
|
V
| F | ||||
·NÚMERO DE LINHAS DE UMA TABELA-VERDADE: Cada proposição simples (atômica) tem dois valores V ou F, que se excluem. Para n atômicas distintas, há tantas possibilidades quantos são os arranjos com repetição de 2 (V e F) elementos n a n. Segue-se que o número de linhas da tabela verdade é 2n. Assim, para duas proposições são 22 = 4 linhas; para 3 proposições são 23 = 8; etc.
Exemplo: a tabela - verdade da fórmula ((p Ù q) ® r) terá 8 linhas como segue :
NOTA: "OU EXCLUSIVO" É importante observar que "ou" pode ter dois sentidos na linguagem habitual: inclusivo(disjunção) Ú ("vel") e exclusivo Ú ( "aut") onde p Úq significa ((p Ú q) Ù~ (p Ù q)).
| ((p Ú q) Ù ~ (p Ù q)) | ||
| V F F V | ||
| V V V F | ||
| V V V F | ||
| F F V F |
CELINA ABAR
Adição e subtração de fração
As adições e subtrações de frações devem respeitar duas condições de operações:
1ª condição: denominadores iguais.
Quando os denominadores são iguais, os numeradores devem ser somados ou subtraídos de acordo com os sinais operatórios e o valor do denominador mantido. Observe os exemplos:
.jpg)
2º condição: denominadores diferentes.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos. O novo denominador deverá ser dividido pelos denominadores atuais, multiplicando o quociente pelo numerador correspondente, constituindo novas frações proporcionalmente iguais as anteriores e com denominadores iguais. Observe os cálculos:
.jpg)
Realizar o MMC entre 3 e 4.
.jpg)
.jpg)
.jpg)
Realizar o MMC entre 5, 9 e 12.
.jpg)
.jpg)
.jpg)
Realizar o MMC entre 15 e 20.
.jpg)
.jpg)
www.mundoeducacao.com.br
1ª condição: denominadores iguais.
Quando os denominadores são iguais, os numeradores devem ser somados ou subtraídos de acordo com os sinais operatórios e o valor do denominador mantido. Observe os exemplos:
.jpg)
2º condição: denominadores diferentes.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos. O novo denominador deverá ser dividido pelos denominadores atuais, multiplicando o quociente pelo numerador correspondente, constituindo novas frações proporcionalmente iguais as anteriores e com denominadores iguais. Observe os cálculos:
.jpg)
Realizar o MMC entre 3 e 4.
.jpg)
.jpg)
.jpg)
Realizar o MMC entre 5, 9 e 12.
.jpg)
.jpg)
.jpg)
Realizar o MMC entre 15 e 20.
.jpg)
.jpg)
www.mundoeducacao.com.br
Salmos 121
Levantarei os meus olhos para os montes, de onde vem o meu socorro.
O meu socorro vem do Senhor que fez o céu e a terra.
Não deixará vacilar o teu pé; aquele que te guarda não tosquenejará.
Eis que não tosquenejará nem dormirá o guarda de Israel.
O Senhor é quem te guarda; o Senhor é a tua sombra à tua direita.
O sol não te molestará de dia nem a lua de noite.
O Senhor te guardará de todo o mal; guardará a tua alma.
O Senhor guardará a tua entrada e a tua saída, desde agora e para sempre.
Salmos 121:1-8
O meu socorro vem do Senhor que fez o céu e a terra.
Não deixará vacilar o teu pé; aquele que te guarda não tosquenejará.
Eis que não tosquenejará nem dormirá o guarda de Israel.
O Senhor é quem te guarda; o Senhor é a tua sombra à tua direita.
O sol não te molestará de dia nem a lua de noite.
O Senhor te guardará de todo o mal; guardará a tua alma.
O Senhor guardará a tua entrada e a tua saída, desde agora e para sempre.
Salmos 121:1-8
Nematelmintos
Os nemaltelmintos eram tratados antigamente como uma classe dentro de filo maior, denominado Aschelminthes. Atualmente não se consideram mais os asquelmintos como um filo verdadeiro, mas apenas um termo genérico sem valor científico. Os nematelmintos possuem corpo cilíndrico, recoberto por uma cutícula resistente, com simetria bilateral. Numerosas espécies apresentam vida livre, porém muitas são parasitas de plantas e animais.
Os nematóideos possuem dois nervos (dorsal e ventral) longitudinais que correm o corpo do animal. Não há sistema circulatório ou respiratório. Possuem sistema digestivo completo e digestão extracelular. A respiração é anaeróbica. Todos apresentam sexos separados.
Algumas espécies parasitam o ser humano: Ascaris lumbricoides, Necator americanus, Enterobius vermiculares, Ancylostoma duodenale , por exemplo.
Ascaris lumbricoides
Ascaris lumbricoides ou lombriga, como é conhecida popularmente, é um verme de 15 a 20 centímetros de comprimento, parasita do intestino humano. Apresenta dimorfismo sexual (macho diferente das fêmeas), sendo que o macho é menor e possui a extremidade posterior do corpo em forma de gancho como podemos ver na figura abaixo:

A lombriga quando adulta vive no intestino humano, onde deposita seus ovos, que são eliminados com as fezes do hospedeiro. Mais tarde esses ovos vão se desenvolver contaminando o solo e as águas dos rios. Esses causam diferentes doenças que atacam diversas partes do corpo humano, podendo levar até mesmo à morte.
Transmissão
Esse verme pode ser pego de várias maneiras como por exemplo, em instalações sanitárias inadequadas. As fezes são liberadas podendo contaminar a água, o solo e conseqüentemente a vegetação. Assim, ao se comer o vegetal contaminado, os ovos podem chegar ao tubo digestivo. Em cada ovo desenvolve-se uma larva que perfura a parede do intestino, atingindo os vasos sangüíneos.
Sintomas
As larvas da lombriga podem trazer graves problemas respiratórios, coceira no nariz e na garganta (3). Já o verme quando adulto causa outras doenças como vômitos, cólicas e convulsões (4). Mas, quando o número de vermes é grande, leva à obstrução intestinal, podendo causar a morte. Nas crianças, às vezes, também aparecem outros sintomas como a asfixia, pois se acumulam na laringe e na faringe, durante o excesso de vômitos.
Profilaxia
Esses vermes são transmissíveis através das fezes depositadas no solo e nas águas dos rios, contaminando assim o alimento plantado naquele local. Logo, a pessoa que ingere esse alimento fica contaminada. Para evitar essa contaminação é preciso ter, principalmente, Saneamento Básico, condições sanitárias adequadas, pois assim as fezes não irão contaminar o meio ambiente. Ao se alimentar, deve-se lavar muito bem os alimentos que serão ingeridos crus. As verduras cruas devem ser bem desinfetadas ou, se possível, cozidas.
Ancylostoma duodenale
Ancilóstomo. Seu nome científico é Ancylostoma duodenale. Esse verme possui aproximadamente 15 milímetros de comprimento. Alimenta-se do sangue da parede do intestino humano, ali permanecendo fixo.

Acima a figura mostra os ganchos da cavidade bucal com os quais o verme se prende à parede do intestino e ao lado o ovo com o embrião.
Sintomas
Ao contrair Amarelão ou Ancilostomose, a pessoa contaminada se enfraquece e pode ter anemia, pois ocorre hemorragia nas feridas da parede intestinal.
Transmissão
As fêmeas do ancilóstomo depositam seus ovos no intestino humano. Ao saírem com as fezes, podem cair em solos úmidos. Esses ovos dão origem a larvas microscópicas, que se fixam na terra. As larvas, ao entrarem em contato com a pele humana, penetram no organismo. Pela circulação, vão para o intestino humano, onde atingem a fase adulta e podem se reproduzir, dando origem a doenças como ancilostomose ou amarelão, como podemos ver abaixo:
Ciclo do Amarelão
Esses vermes são encontrados especialmente nas areias úmidas e em poças d'água.

Profilaxia
Precisamos ter alguns cuidados básicos como:
Os nematóideos possuem dois nervos (dorsal e ventral) longitudinais que correm o corpo do animal. Não há sistema circulatório ou respiratório. Possuem sistema digestivo completo e digestão extracelular. A respiração é anaeróbica. Todos apresentam sexos separados.
Algumas espécies parasitam o ser humano: Ascaris lumbricoides, Necator americanus, Enterobius vermiculares, Ancylostoma duodenale , por exemplo.
Ascaris lumbricoides
Ascaris lumbricoides ou lombriga, como é conhecida popularmente, é um verme de 15 a 20 centímetros de comprimento, parasita do intestino humano. Apresenta dimorfismo sexual (macho diferente das fêmeas), sendo que o macho é menor e possui a extremidade posterior do corpo em forma de gancho como podemos ver na figura abaixo:

A lombriga quando adulta vive no intestino humano, onde deposita seus ovos, que são eliminados com as fezes do hospedeiro. Mais tarde esses ovos vão se desenvolver contaminando o solo e as águas dos rios. Esses causam diferentes doenças que atacam diversas partes do corpo humano, podendo levar até mesmo à morte.
Transmissão
Esse verme pode ser pego de várias maneiras como por exemplo, em instalações sanitárias inadequadas. As fezes são liberadas podendo contaminar a água, o solo e conseqüentemente a vegetação. Assim, ao se comer o vegetal contaminado, os ovos podem chegar ao tubo digestivo. Em cada ovo desenvolve-se uma larva que perfura a parede do intestino, atingindo os vasos sangüíneos.
Sintomas
As larvas da lombriga podem trazer graves problemas respiratórios, coceira no nariz e na garganta (3). Já o verme quando adulto causa outras doenças como vômitos, cólicas e convulsões (4). Mas, quando o número de vermes é grande, leva à obstrução intestinal, podendo causar a morte. Nas crianças, às vezes, também aparecem outros sintomas como a asfixia, pois se acumulam na laringe e na faringe, durante o excesso de vômitos.
Profilaxia
Esses vermes são transmissíveis através das fezes depositadas no solo e nas águas dos rios, contaminando assim o alimento plantado naquele local. Logo, a pessoa que ingere esse alimento fica contaminada. Para evitar essa contaminação é preciso ter, principalmente, Saneamento Básico, condições sanitárias adequadas, pois assim as fezes não irão contaminar o meio ambiente. Ao se alimentar, deve-se lavar muito bem os alimentos que serão ingeridos crus. As verduras cruas devem ser bem desinfetadas ou, se possível, cozidas.
Ancylostoma duodenale
Ancilóstomo. Seu nome científico é Ancylostoma duodenale. Esse verme possui aproximadamente 15 milímetros de comprimento. Alimenta-se do sangue da parede do intestino humano, ali permanecendo fixo.

Acima a figura mostra os ganchos da cavidade bucal com os quais o verme se prende à parede do intestino e ao lado o ovo com o embrião.
Sintomas
Ao contrair Amarelão ou Ancilostomose, a pessoa contaminada se enfraquece e pode ter anemia, pois ocorre hemorragia nas feridas da parede intestinal.
Transmissão
As fêmeas do ancilóstomo depositam seus ovos no intestino humano. Ao saírem com as fezes, podem cair em solos úmidos. Esses ovos dão origem a larvas microscópicas, que se fixam na terra. As larvas, ao entrarem em contato com a pele humana, penetram no organismo. Pela circulação, vão para o intestino humano, onde atingem a fase adulta e podem se reproduzir, dando origem a doenças como ancilostomose ou amarelão, como podemos ver abaixo:
Ciclo do Amarelão
Esses vermes são encontrados especialmente nas areias úmidas e em poças d'água.

Profilaxia
Precisamos ter alguns cuidados básicos como:
- Não devemos jogar fezes no meio ambiente, pois assim podemos contaminá-lo.
- Devemos ter Saneamento Básico, desviando as fezes para locais específicos, para não contaminar o ambiente.
- Evitar o contato da pele humana com terra suja ou que possa estar contaminada. Usar calçados ajuda a prevenir a contaminação desses vermes.
quinta-feira, 23 de julho de 2020
Elipse
Definição: Dados dois pontos
quaisquer do plano F1 e F2 e seja 2c a distância entre eles, elipse é o
conjunto dos pontos do plano cuja soma das distâncias à F1 e F2 é a
constante 2a (2a > 2c).
Elementos da Elipse:

F1 e F2 → são os focos
C → Centro da elipse
2c → distância focal
2a → medida do eixo maior
2b → medida do eixo menor
c/a → excentricidade
Há uma relação entre os valores a, b e c→ a2 = b2+c2
Equação da Elipse.
1º caso: Elipse com focos sobre o eixo x.

Nesse caso, os focos têm coordenadas F1( - c , 0) e F2(c , 0). Logo, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo x será:

2º Caso: Elipse com focos sobre o eixo y.

Nesse caso, os focos apresentam coordenadas F1(0 , -c) e F2(0 , c). Assim, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo y será:

Exemplo 1. Determine a equação reduzida da elipse com focos sobre o eixo x, com eixo maior medindo 12 e eixo menor 8.
Solução: temos que
2a = 12 → a =6
2b = 8 → b = 4
Assim,

Exemplo 2. Determine a equação reduzida da elipse sabendo que um dos focos é F1(0 , -3) e que o eixo menor mede 8.
Solução: temos que
Se F1(0 , -3) → c = 3 e o foco está sobre o eixo y.
2b = 8 → b = 4
Usando a relação notável: a2 = b2+c2, obtemos:
a2 = 42+32 → a2 = 16 + 9 → a2 = 25 → a = 5
Assim, a equação reduzida da elipse será:
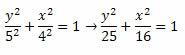
Marcelo Rigonatto
Elementos da Elipse:
F1 e F2 → são os focos
C → Centro da elipse
2c → distância focal
2a → medida do eixo maior
2b → medida do eixo menor
c/a → excentricidade
Há uma relação entre os valores a, b e c→ a2 = b2+c2
Equação da Elipse.
1º caso: Elipse com focos sobre o eixo x.

Nesse caso, os focos têm coordenadas F1( - c , 0) e F2(c , 0). Logo, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo x será:

2º Caso: Elipse com focos sobre o eixo y.
Nesse caso, os focos apresentam coordenadas F1(0 , -c) e F2(0 , c). Assim, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo y será:

Exemplo 1. Determine a equação reduzida da elipse com focos sobre o eixo x, com eixo maior medindo 12 e eixo menor 8.
Solução: temos que
2a = 12 → a =6
2b = 8 → b = 4
Assim,

Exemplo 2. Determine a equação reduzida da elipse sabendo que um dos focos é F1(0 , -3) e que o eixo menor mede 8.
Solução: temos que
Se F1(0 , -3) → c = 3 e o foco está sobre o eixo y.
2b = 8 → b = 4
Usando a relação notável: a2 = b2+c2, obtemos:
a2 = 42+32 → a2 = 16 + 9 → a2 = 25 → a = 5
Assim, a equação reduzida da elipse será:
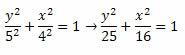
Marcelo Rigonatto
Transformações Lineares
1. Se T : V → W é uma transformação linear, mostre que:
(a) Ker(T) é um subespaço de V . (b) Im(T) é um subespaço de W.
Solução:





 Agora, somando-se membro a membro estas duas equações vetoriais, vem
Agora, somando-se membro a membro estas duas equações vetoriais, vem


 fazendo
v = λu ∈ V . Isto é, existe v ∈ V tal que λw = T(v), basta tomarmos v =
λu ∈ V e, portanto, λw ∈ Im(T). Daí, concluímos que Im(T) é um
subespaço vetorial de W.
fazendo
v = λu ∈ V . Isto é, existe v ∈ V tal que λw = T(v), basta tomarmos v =
λu ∈ V e, portanto, λw ∈ Im(T). Daí, concluímos que Im(T) é um
subespaço vetorial de W.
(a) Determine uma base do núcleo de T. (b) Dê a dimensão da imagem de T. (c) T é sobrejetora? Justifique. (d) Faça um esboço de Ker(T) e Im(T).
Solução:


 (c) Não. A imagem não é igual ao contradomínio já que DimIm(T) = 2 e o contradomínio tem dimensão 3.
(c) Não. A imagem não é igual ao contradomínio já que DimIm(T) = 2 e o contradomínio tem dimensão 3.
3. No plano, uma rotação anti-horária de 45◦ é seguida por uma dilatação de √ 2. Ache a aplicação
A que representa esta trasnformação do plano.
Solução:
sinθ cosθ
Que pode ser escrito como uma transformação:
 Uma dilatação D de √
Uma dilatação D de √
2(x,y). Como queremos dilatar a transformação R, teremos
 Solução: Escreva
Solução: Escreva
Aplicando T e sabendo que ela é linear, temos:


 Solução: (a) Podemos escrever essa transformação na forma:
Solução: (a) Podemos escrever essa transformação na forma:
 (b) Para a imagem, teremos
(b) Para a imagem, teremos
 6. Mostrar que a matriz do operador linear indentidade
6. Mostrar que a matriz do operador linear indentidade
I : Rn → Rn,I(v) = v em uma base qualquer, é a matriz identidade n × n.
Solução:
Daí, a matriz de transformação será

 Solução: Escreva a combinação
Solução: Escreva a combinação
Como T é linear,
Sendo T injetiva, é L.I.
(d) Ache a transformação linear P : R2 → R2 tal que P = S ◦ T
Solução:

 ou seja,
ou seja,
(c)

 ou seja,
ou seja,
(d)
Solução:

 10. Seja T : V → W uma transformação. Mostre que se T é linear, então T(0) = 0.
10. Seja T : V → W uma transformação. Mostre que se T é linear, então T(0) = 0.


(a) Ker(T) é um subespaço de V . (b) Im(T) é um subespaço de W.
Solução:
(a) Determine uma base do núcleo de T. (b) Dê a dimensão da imagem de T. (c) T é sobrejetora? Justifique. (d) Faça um esboço de Ker(T) e Im(T).
Solução:

3. No plano, uma rotação anti-horária de 45◦ é seguida por uma dilatação de √ 2. Ache a aplicação
A que representa esta trasnformação do plano.
Solução:
sinθ cosθ
Que pode ser escrito como uma transformação:

2(x,y). Como queremos dilatar a transformação R, teremos
Aplicando T e sabendo que ela é linear, temos:
| α1 = α2 = | = αm = 0. |



I : Rn → Rn,I(v) = v em uma base qualquer, é a matriz identidade n × n.
Solução:
| T(v1) = 1 · v1 + 0 · v2 + | 0 · vn |
| T(v2) = 0 · v1 + 1 · v2 + | + 0 · vn |
| T(vn) = 0 · v1 + 0 · v2 + | + 1 · vn |
| a1 · Tu1 + a2 · Tu2 + | + ak · Tuk = 0(= T(0)) |
| T(a1 · u1 + a2 · u2 + | + ak · uk) = T(0). |
| a1 · u1 + a2 · u2 + | + ak · uk = 0. |
| Como u1,u2,...,uk são vetores LI, teremos a1 = a2 = | = ak = 0, e portanto {T(u1),...,T(uk)} |
(d) Ache a transformação linear P : R2 → R2 tal que P = S ◦ T
Solução:

(c)

(d)
Solução:

fonte http://www.ebah.com.br
Assinar:
Comentários (Atom)






