Elipse

Definição: Dados dois pontos quaisquer do plano F1 e F2 e seja 2c a distância entre eles, elipse é o conjunto dos pontos do plano cuja soma das distâncias à F1 e F2 é a constante 2a (2a > 2c).

Elementos da Elipse:


F1 e F2 → são os focos
C → Centro da elipse
2c → distância focal
2a → medida do eixo maior
2b → medida do eixo menor
c/a → excentricidade

Há uma relação entre os valores a, b e c→ a² = b²+c²

Equação da Elipse.

1º caso: Elipse com focos sobre o eixo x.

Nesse caso, os focos têm coordenadas F1( - c , 0) e F2(c , 0). Logo, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo x será:


2º Caso: Elipse com focos sobre o eixo y.

Nesse caso, os focos apresentam coordenadas F1(0 , -c) e F2(0 , c). Assim, a equação reduzida da elipse com centro na origem do sistema cartesiano e com focos sobre o eixo y será:

Exemplo 1. Determine a equação reduzida da elipse com focos sobre o eixo x, com eixo maior medindo 12 e eixo menor 8.

Solução: temos que
2a = 12 → a =6
2b = 8 → b = 4
Assim,


Exemplo 2. Determine a equação reduzida da elipse sabendo que um dos focos é F1(0 , -3) e que o eixo menor mede 8.

Solução: temos que
Se F1(0 , -3) → c = 3 e o foco está sobre o eixo y.
2b = 8 → b = 4
Usando a relação notável: a² = b²+c², obtemos:
a² = 4²+3² → a² = 16 + 9 → a² = 25 → a = 5
Assim, a equação reduzida da elipse será:

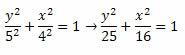
  Marcelo Rigonatto