Equações logarítmicas

Existem quatro tipos básicos de equações logarítmicas. Iremos resolver um exemplo de cada tipo.

Tipo 1. Equação que envolve a igualdade entre dois logaritmos de mesma base.

A solução é dada fazendo x = y > 0
Exemplo: Resolva a equação


Solução: temos que
2x + 4 = 3x + 1
2x – 3x = 1 – 4
– x = – 3
x = 3
Portanto, S = { 3 }

Tipo 2. Equação que envolve a igualdade entre um logaritmo e um número.

A solução é dada por x = a^c.

Exemplo: Encontre a solução da equação

Solução: Pela definição de logaritmo temos:

5x + 2 = 3³
5x + 2 = 27
5x = 27 – 2
5x = 25
x = 5

Portanto S = {5}.

Tipo 3. Equação que é necessário fazer uma mudança de incógnita.
Exemplo: Resolva a equação

Solução: Vamos fazer a seguinte mudança de incógnita

Substituindo na equação inicial, ficaremos com:

Tipo 4. Equações que utilizam as propriedades do logaritmo ou de mudança de base.

Exemplo: Resolva a equação


Solução: usando as propriedades do logaritmo, podemos reescrever a equação acima da seguinte forma:

Note que para isso utilizamos as seguintes propriedades:

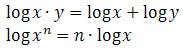
Vamos retornar à equação:

Como ficamos com uma igualdade entre dois logaritmos, segue que:
(2x +3)(x + 2) = x²
ou
2x² + 4x + 3x + 6 = x²
2x² – x² + 7x + 6 = 0
x² + 7x + 6 = 0


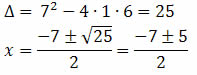
x = -1 ou x = - 6

Lembre-se que para o logaritmo existir o logaritmando e a base devem ser positivos.
Com os valores encontrados para x, o logaritmando ficará negativo. Sendo assim, a equação não tem solução ou S = ø.
Por Marcelo Rigonatto