Operações com conjuntos

Operações envolvendo conjuntos

As operações envolvendo conjuntos são de fundamental importância para o desenvolvimento de outras áreas da matemática, como a probabilidade, por exemplo; e para resolução de diversas situações-problema. Dentre as operações entre conjuntos, destacamos: a união, intersecção, diferença e complementar de um conjunto. Vejamos como efetuar cada uma delas.

1. União de conjuntos.

Dados dois conjuntos A e B, a união de A com B é o conjunto formado pelos elementos que pertencem ao conjunto A ou ao conjunto B.



Exemplo: Considerando os conjuntos A = {1, 3, 5, 7, 9, 11} e B = {8, 9, 10, 11, 12}, temos que:

A U B = {1, 3, 5, 7, 8, 9, 10, 11, 12}

2. Intersecção de conjuntos.

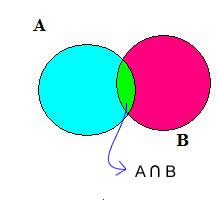
Dados dois conjuntos A e B, a intersecção de A com B é o conjunto formado pelos elementos que pertencem ao conjunto A e ao conjunto B. De uma forma mais simples, é o conjunto formado pelos elementos que são comuns aos dois conjuntos.


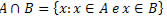
Exemplo 1: Seja A = {1, 3, 5, 7, 9, 11} e B = {8, 9, 10, 11, 12}, temos que:

A ∩ B = {9, 11}

Exemplo 2. A = {1, 3, 5, 7, 9, 11} e C = {2, 4, 6, 8, 10}

A ∩ C = ø, pois os dois conjuntos não apresentam elementos em comum.

A operação de intersecção apresenta algumas propriedades:

a) Propriedade reflexiva.
A ∩ A = A

b) Propriedade comutativa.
A ∩ B = B ∩ A

c) Propriedade associativa.
A ∩ (B ∩ C) = (A ∩ B) ∩ C

d) Propriedade distributiva.
A ∩ (B U C) = (A ∩ B) U (A ∩ C)
A U (B ∩ C) = (A U B) ∩ (A U C)

Graficamente, utilizando os diagramas de Venn, podemos representar a operação de intersecção da seguinte forma:

3. Diferença de conjuntos.

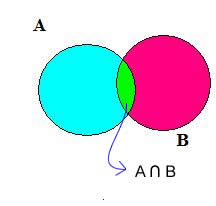
Dados dois conjuntos A e B, a diferença entre A e B é o conjunto formado pelos elementos de A que não pertencem a B.



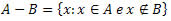
Exemplo: A = {1, 3, 5, 7, 9, 11} e B = {8, 9, 10, 11, 12}

A – B = {1, 3, 5, 7}
B – A = {8, 10, 12}

4. Complementar de um conjunto.

Essa operação é um caso particular de diferença entre conjuntos. Considere dois conjuntos, A e B, sendo que B está contido em A 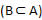, ou seja, B é um subconjunto de A. O complementar de B em relação a A, representado por C_AB, é a diferença A – B.

Exemplo: Sejam A = {2, 4, 6, 8, 10, 12, 14} e B = {4, 8, 12}, temos que:

C_AB = A – B = {2, 6, 10, 14}

Marcelo Rigonatto