Equação Geral da Reta

Para determinarmos a equação geral de uma reta utilizamos os conceitos relacionados a matrizes. Na determinação da equação na forma ax + by + c = 0 aplicamos a regra de Sarrus utilizada na obtenção do discriminante de uma matriz quadrada de ordem 3 x 3. Para utilizarmos uma matriz nessa determinação da equação feral devemos ter no mínimo dois pares ordenados (x,y) dos possíveis pontos alinhados, por onde a reta irá passar. Observe a matriz geral da determinação da equação geral:

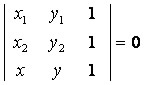
Na matriz temos os pares ordenados que devem ser informados: (x₁, y₁) e (x₂, y₂) e um ponto genérico representado pelo par (x, y). Observe que a 3º coluna da matriz é completada com o algarismo 1. Vamos aplicar esses conceitos na obtenção da equação geral da reta que passa pelos pontos A(1, 2) e B(3,8), veja:

Ponto A temos que: x₁ = 1 e y₁ = 2
Ponto B temos que: x₂ = 3 e y₂ = 8
Ponto genérico C representado pelo par ordenado (x, y)


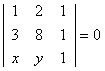
Calcular o determinante de uma matriz quadrada aplicando a regra de Sarrus significa:

1º passo: repetir a 1º e a 2º coluna da matriz.

2º passo: somar os produtos dos termos da diagonal principal.

3º passo: somar os produtos dos termos da diagonal secundária.

4º passo: subtrair a soma total dos termos da diagonal principal dos termos da diagonal secundária.
Observe todos os passos na resolução da matriz dos pontos da reta:

[(1 * 8 * 1) + (2 * 1 *x) + (1 * 3 * y)] – [(2 * 3 * 1) + (1 * 1 * y) + (1 * 8 * x)] = 0
[ 8 + 2x + 3y] – [6 + y + 8x] = 0
8 + 2x + 3y – 6 – y – 8x = 0
2x – 8x + 3y – y + 8 – 6 = 0
–6x + 2y + 2 = 0

Os pontos A(1, 2) e B(3,8) pertencem a seguinte equação geral da reta: –6x + 2y + 2 = 0.

Exemplo 2
Vamos determinar a equação geral da reta que passa pelos pontos: A(–1, 2) e B(–2, 5).


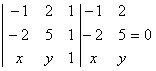
[– 5 + 2x + (–2y)] – [(– 4) + (– y) + 5x] = 0
[– 5 + 2x – 2y] – [– 4 – y + 5x] = 0
– 5 + 2x – 2y + 4 + y – 5x = 0
–3x – y – 1 = 0
A equação geral da reta que passa pelos pontos A(–1, 2) e B(–2, 5) é dada pela expressão: –3x – y – 1 = 0.

Por Marcos Noé