Área da Região Triangular em Relação as Coordenadas dos Vértices

Podemos determinar a área de uma região triangular utilizando expressões relacionadas à Geometria Plana. Nas situações envolvendo coordenadas de posicionamento dos vértices de um triângulo, os cálculos são efetuados de acordo com o determinante de uma matriz quadrada, formada pelos valores das coordenadas dos pontos de posicionamento. A matriz construída deverá conter em uma de suas colunas os valores das abscissas e em outra, os valores das ordenadas dos pontos, uma terceira coluna será completada com valores iguais a 1.

A área do triângulo será determinada pela metade do valor da determinante. Veja:

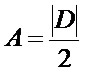
Os vértices de um triângulo possuem as seguintes coordenadas de localização: A(–1, 1), B(4,0) e C(–3, 3). Vamos determinar a área dessa região triangular utilizando os princípios do determinante de uma matriz.

Aplicando Sarrus

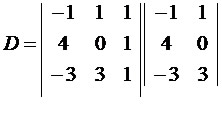
Diagonal principal
(–1) * 0 * 1 = 0
1 * 1 * (–3) = –3
1 * 4 * 3 = 12

Soma: 0 – 3 + 12 = 9

Diagonal secundária
1 * 0 * (–3) = 0
(–1) * 1 * (3) = – 3
1 * 4 * 1 = 4

Soma: 0 – 3 + 4 = 1

D = (Somatório do produto dos elementos da diagonal principal) – (Somatório do produto dos elementos da diagonal secundária)

D = 9 – 1
D = 8

A = |D| / 2
A = 8 / 2
A = 4

A área da região triangular com os vértices localizados nos pontos A(–1, 1), B(4,0) e C(–3, 3) corresponde a 4 unidades de área.

  Marcos Noé