Calculo da matriz inversa por meio de determinantes

A determinação de uma matriz inversa de ordem n é dada através da multiplicação por uma matriz B genérica, sendo que o resultado deverá ser uma matriz identidade. Lembrando que matriz identidade de ordem n é uma matriz onde a diagonal principal é preenchida pelo número 1 e os demais espaços são preenchidos com o número 0.

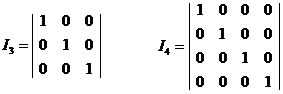
Exemplos de uma Matriz Identidade:

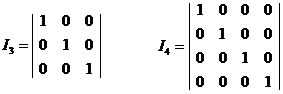
A matriz B será representada por uma matriz genérica de mesmo número de colunas e linhas.

Exemplo 1


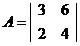Vamos determinar, se existir, a inversa da matriz .

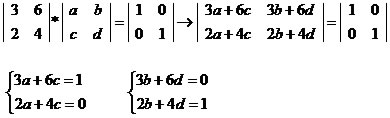
Os sistemas não possuem resolução, são impossíveis. Nesse tipo de situação, onde os sistemas não podem ser solucionados, chegamos à conclusão que a matriz A não possui inversa.


Exemplo 2

Determine, se existir, a inversa da matriz .

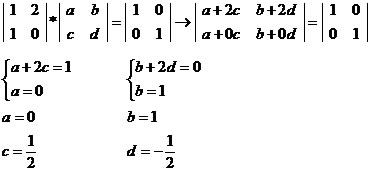
a + 2c = 1
a = 0

b + 2d = 0
b = 1
Portanto, a matriz inversa de é .
www.mundoeducacao.com.br