Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
As funções possuem algumas propriedades que as caracterizam f : A→B.
Função sobrejetora
Função injetora
Função bijetora
Função inversa
Função sobrejetora: uma função é sobrejetora se, e somente se, o seu conjunto imagem for especificadamente igual ao contradomínio, Im = B. Por exemplo, se temos uma função f : Z→Z definida por y = x +1 ela é sobrejetora, pois Im = Z.
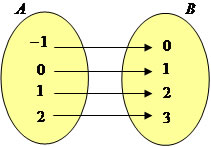
Função sobrejetora
Função injetora
Função bijetora
Função inversa
Função sobrejetora: uma função é sobrejetora se, e somente se, o seu conjunto imagem for especificadamente igual ao contradomínio, Im = B. Por exemplo, se temos uma função f : Z→Z definida por y = x +1 ela é sobrejetora, pois Im = Z.

Função injetora: uma função é injetora se os elementos distintos do domínio tiverem imagens distintas. Por exemplo, dada a função f : A→B, tal que f(x) = 3x.
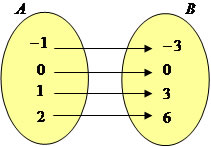
Função bijetora: uma função é bijetora se ela é injetora e sobrejetora. Por exemplo, a função f : A→B, tal que f(x) = 5x + 4.
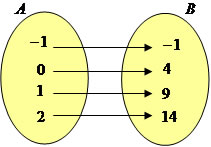

Função bijetora: uma função é bijetora se ela é injetora e sobrejetora. Por exemplo, a função f : A→B, tal que f(x) = 5x + 4.

Note que ela é injetora, pois x1≠x2 implica em f(x1) ≠f(x2)
É sobrejetora, pois para cada elemento em B existe pelos menos um em A, tal que f(x)=y.
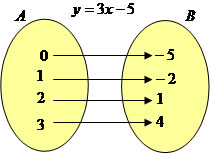
Função inversa: uma função será inversa se ela for bijetora. Se f : A→B é considerada bijetora então ela admite inversa f : B→A. Por exemplo, a função y = 3x-5 possui inversa y = (x+5)/3.
É sobrejetora, pois para cada elemento em B existe pelos menos um em A, tal que f(x)=y.
Função inversa: uma função será inversa se ela for bijetora. Se f : A→B é considerada bijetora então ela admite inversa f : B→A. Por exemplo, a função y = 3x-5 possui inversa y = (x+5)/3.

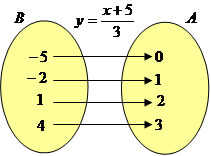
Podemos estabelecer a seguinte diagramação:
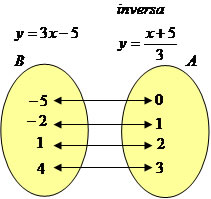
Note que a função possui relação de A→B e de B→A, então podemos dizer que ela é inversa.
Marcos Noé
Nenhum comentário:
Postar um comentário