terça-feira, 7 de abril de 2020
Condições de existência de uma equação do 2º grau através de restrições
Uma equação do 2º grau possui algumas condições de existência envolvendo o valor do discriminante. Os coeficientes de uma equação quadrática determinam os possíveis resultados, por exemplo:
Caso o valor do discriminante seja maior que zero, a equação terá duas raízes reais e diferentes.
O discriminante possuindo valor menor que zero, indica que a equação não possui raízes reais.
Nas situações em que o discriminante assume valor igual a zero, a equação possui apenas uma raiz real.
Vamos desenvolver alguns exemplos relacionados às condições de existência e restrições de uma equação do 2º grau:
Exemplo 1
Determine o valor de k, considerando que a equação 2x² + 4x + 5k = 0 , tenha duas raízes reais e distintas.
Coeficientes:
a = 2, b = 4 e c = 5k
a) duas raízes reais e distintas
Caso o valor do discriminante seja maior que zero, a equação terá duas raízes reais e diferentes.
O discriminante possuindo valor menor que zero, indica que a equação não possui raízes reais.
Nas situações em que o discriminante assume valor igual a zero, a equação possui apenas uma raiz real.
Vamos desenvolver alguns exemplos relacionados às condições de existência e restrições de uma equação do 2º grau:
Exemplo 1
Determine o valor de k, considerando que a equação 2x² + 4x + 5k = 0 , tenha duas raízes reais e distintas.
Coeficientes:
a = 2, b = 4 e c = 5k
a) duas raízes reais e distintas
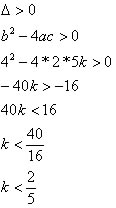
S = {k Є R / k < 2/5}
Exemplo 2
Vamos determinar o valor de p na seguinte equação: x² – (p + 5)x + 36 = 0, de forma que a equação possua raízes reais e iguais.
Coeficientes:
a = 1
b = p + 5
c = 36
a) raízes reais e iguais
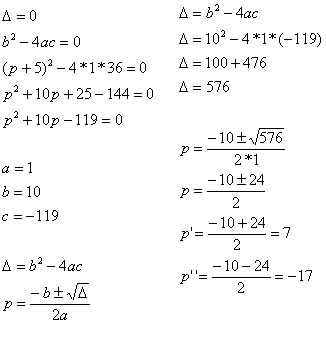
S = {p Є R / p = 7 e p = –17}
fonte;mundoeducacao.com.br
Fração geratriz
A fração geratriz, quando representada na forma decimal, produz dízimas periódicas simples ou compostas. Portanto, toda dízima periódica (número decimal) deve possuir uma forma fracionária, por isso demonstraremos como transformar números decimais em frações geratrizes. Primeiro vamos observar alguns exemplos de números racionais com períodos:
0,33333333... , período 3 (um algarismo)
0,23232323..., período 23 (dois algarismos)
0,562562562..., período 562 (três algarismos)
Para encontrarmos a fração geratriz seguimos os seguintes passos.
1º passo – relacionar a dízima periódica com uma incógnita
x = 0,333333...
2º passo – multiplicar os dois lados da igualdade por um múltiplo de 10, de acordo com a quantidade de algarismos do período, por exemplo:
um algarismo, multiplicar por 10
dois algarismos, multiplicar por 100
três algarismos, multiplicar por 1000, e assim sucessivamente.
x = 0,333333 ... * 10
10x = 3,3333 ...
3º passo – subtrair a segunda igualdade da primeira igualdade
10x = 3,3333
– x = 0,3333
9x = 3
9x = 3
x = 3/9
Exemplo 2
Encontrar a fração geratriz da seguinte dízima periódica: 0,232323... .
1º passo
x = 0,232323....
2º passo
x = 0,232323 ... * 100
100x = 23,23
3º passo
100x = 23,23
– x = 0,23
99x = 23
99x = 23
x = 23/99
Exemplo 3
Determinar a fração geratriz do número racional 0,562562...
1º passo
x = 0,562562...
2º passo
x = 0,562562... * 1000
1000x = 562,562
3º passo
1000x = 562,562
– x = 0,562
999x = 562
x = 562/999
0,33333333... , período 3 (um algarismo)
0,23232323..., período 23 (dois algarismos)
0,562562562..., período 562 (três algarismos)
Para encontrarmos a fração geratriz seguimos os seguintes passos.
1º passo – relacionar a dízima periódica com uma incógnita
x = 0,333333...
2º passo – multiplicar os dois lados da igualdade por um múltiplo de 10, de acordo com a quantidade de algarismos do período, por exemplo:
um algarismo, multiplicar por 10
dois algarismos, multiplicar por 100
três algarismos, multiplicar por 1000, e assim sucessivamente.
x = 0,333333 ... * 10
10x = 3,3333 ...
3º passo – subtrair a segunda igualdade da primeira igualdade
10x = 3,3333
– x = 0,3333
9x = 3
9x = 3
x = 3/9
Exemplo 2
Encontrar a fração geratriz da seguinte dízima periódica: 0,232323... .
1º passo
x = 0,232323....
2º passo
x = 0,232323 ... * 100
100x = 23,23
3º passo
100x = 23,23
– x = 0,23
99x = 23
99x = 23
x = 23/99
Exemplo 3
Determinar a fração geratriz do número racional 0,562562...
1º passo
x = 0,562562...
2º passo
x = 0,562562... * 1000
1000x = 562,562
3º passo
1000x = 562,562
– x = 0,562
999x = 562
x = 562/999
Sistema de Equações do 1º Grau Metodo de Comparação
Professor de Matemática Antonio Carlos Carneiro Barroso
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
extraído do www.colegioweb.com.br
Este método consiste em isolar uma incógnita numa equação e a mesma incógnita na outra, depois basta igualar as duas, recaindo-se numa equação do 1º grau com uma única incógnita. Exemplo:
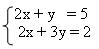
1º passo: vamos isolar o y na primeira e na segunda equação equação para podermos igualar as equações.
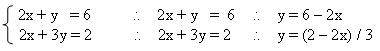
2º passo: igualar as duas equações para encontrar o valor de x.
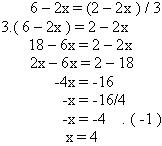
3º passo: Substituir x = 4 em y = 6 – 2x, para encontrar o valor de y.
y = 6 – 2x
y = 6 – 2.4
y = 6 – 8
y = -2
4º passo: dar a solução do sistema.
S = { (4, -2) }
Como podemos observar, independente do método, a solução é a mesma. Então basta escolher o método que seja mais rápido e seguro.
1º passo: vamos isolar o y na primeira e na segunda equação equação para podermos igualar as equações.
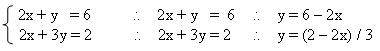
2º passo: igualar as duas equações para encontrar o valor de x.
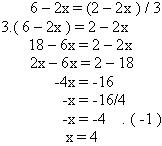
3º passo: Substituir x = 4 em y = 6 – 2x, para encontrar o valor de y.
y = 6 – 2x
y = 6 – 2.4
y = 6 – 8
y = -2
4º passo: dar a solução do sistema.
S = { (4, -2) }
Como podemos observar, independente do método, a solução é a mesma. Então basta escolher o método que seja mais rápido e seguro.
EQUAÇÕES INCOMPLETAS DO 2º GRAU
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2º grau
1º CASO: Equação da forma ax² + c = 0
Exemplos:
Resolver as seguintes equações, sendo U = R
1) x² - 25 = 0
x² = 25
x = + ou - √ 25
x = + ou – 5
Logo : V = { +5, -5}
2) 2x² - 18 = 0
2x²= 18
x² = 18 / 2
x² = 9
x = + ou - √9
x = + ou – 3
Logo V = { +3, -3}
3) 7x²- 14 = 0
7x²= 14
x²= 14/ 7
x² = 2
x = + ou - √2
Logo V = { +√2, -√2}
4) x ²+ 25 = 0
x²= -25
x = + ou - √-25 = nenhum real, pois (nenhum real)² = -25
Logo V = vazio
EXERCÍCIOS
1) Resolva as seguintes equações do 2º grau , sendo U = R
a) x²- 49 = 0 (R: 7, -7)
b) x² = 1 (R: 1, -1)
c) 2x² - 50 = 0 (R: 5, -5)
d) 7x² - 7 = 0 (R: 1, -1)
e) 4x²= 36 (R: 3, -3) ( marcar)
f) 5x² - 15 = 0 (R: √3, -√3)
g) 21 = 7x² (R: √3, -√3)
h) 5x² + 20 = 0 (R: vazio)
i) 4x² - 49 = 0 ( R: 7/2, -7/2)
j) 16 = 9x² (R: 4/3 , -4/3)
k) 3x² + 30 = 0 (R: vazio)
l) 9x² - 5 = 0 (R: √5/3 , -√5/3)
2) Resolva as equações do 2º grau, sendo U = R
a) 7x² + 2 = 30 (R: 2, -2)
b) 2x² - 90 = 8 (R: 7, -7)
c) 4x²- 27 = x² (R: 3, -3)
d) 8x² = 60 – 7x² (R: 2, -2)
3) Resolva as equações do 2º grau, sendo U = R
a) 3 (x² - 1) = 24 (R: 3, -3)
b) 2( x² - 1) = x² + 7 (R: 3, -3)
c) 5(x² - 1) = 4(x² + 1) (R: 3, -3)
d) (x -3) (x – 4) + 8 = x (R: 2, -2)
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
movimento uniforme exercicios
Exercícios sobre movimento uniforme
Testes:
01. A luz solar gasta 5,0 . 102 s para chegar à Terra. O diâmetro do Sol é da ordem de 1,4 . 106 km. Seja 10n a ordem de grandeza do número de corpos idênticos ao Sol que cabem no espaço entre o Sol e a Terra, com centros na reta que una o centro do Sol ao centro da Terra. O valor de n é:
a) 1
b) 2
c) 3
d) 4
e) 10
02. Abaixo estão representados, exatamente como foram obtidos, 5 pedaços de fita, marcados por uma "campainha" que os fere periodicamente e com uma freqüência constante. Estas fitas foram puxadas pela mão, no sentido assinalado, representando, portanto, a velocidade da mão do observador.
Qual das fitas representa, no intervalo de tempo considerado (10 tiques), o movimento que tem velocidade escalar média maior?
a) I
b) II
c) III
d) IV
e) V
03. (FUND. CARLOS CHAGAS) Um trem de 200m de comprimento, com velocidade escalar constante de 60 km/h, gasta 36s para atravessar completamente uma ponte. A extensão da ponte, em metros, é de:
a) 200
b) 400
c) 500
d) 600
e) 800
Para as questões 04 e 05
Dois pontos materiais A e B caminham sobre uma mesma reta e no mesmo sentido. na origem dos tempos a distância entre os pontos é de 5,0 km. A velocidade escalar de A é de 80 km/h e a velocidade escalar de B é de 60 km/h, mantidas constantes.
04. A velocidade escalar de A relativa a B é igual a:
a) zero;
b) 80 km/h;
c) -20 km/h
d) 20 km/h
e) -80 km/h
05. A encontra B:
a) no instante t = 15 h;
b) no instante t = 15 min;
c) no instante t = 1/4 min;
d) nunca
e) n.d.a
Para as questões 06 e 07
Dois pontos materiais A e B caminham sobre uma mesma reta e no mesmo sentido. na origem dos tempos a distância entre os pontos é de 5,0 km. A velocidade escalar de A é de 80 km/h e a velocidade escalar de B é de 60 km/h, mantidas constantes.
06. A função horária que descreve o movimento de B, relativo a A para s em km e t em h, é representada por:
a) s = 5,0 - 20t
b) s = 5,0 + 20 t
c) s = 20t
d) s = -20t
e) n.d.a.
07. A função horária que descreve o movimento de A, relativo a B para s em km e t em h, é representada por:
a) s = -5,0 - 20t
b) s = 5,0 + 20 t
c) s = 20t - 5,0
d) s = -20t
e) n.d.a.
08. Considere dois trens T1 e T2 caminhando em linhas férreas retilíneas e paralelas com velocidades de intensidade V1 = 36 km/h e V2 = 72 km/h, em sentidos opostos. Um observador O1 está no trem T1 e nota que a passagem de T2, diante de sua janela, durou um intervalo de tempo de 10s. O tempo gasto por T2, para passar por um túnel de comprimento 200m, é de:
a) 25s
b) 20s
c) 30s
d) 50s
e) 60s
Para as questões 09 e 10
Considere um movimento cuja posição s, em função do tempo t, está representado no gráfico.
09. A distância percorrida pelo móvel entre os instantes t = 0 e t = 20s, em metros, vale:
a) -40
b) zero
c) 20
d) 40
e) 80
10. O móvel passa pela origem no instante:
a) zero
b) 5,0s
c) 10s
d) 15s
e) 20s
Resolução:
01 - B
02 - A 03 - B
04 - D
05 - B
06 - A 07 - C
08 - A
09 - E
10 - C
Testes:
01. A luz solar gasta 5,0 . 102 s para chegar à Terra. O diâmetro do Sol é da ordem de 1,4 . 106 km. Seja 10n a ordem de grandeza do número de corpos idênticos ao Sol que cabem no espaço entre o Sol e a Terra, com centros na reta que una o centro do Sol ao centro da Terra. O valor de n é:
a) 1
b) 2
c) 3
d) 4
e) 10
02. Abaixo estão representados, exatamente como foram obtidos, 5 pedaços de fita, marcados por uma "campainha" que os fere periodicamente e com uma freqüência constante. Estas fitas foram puxadas pela mão, no sentido assinalado, representando, portanto, a velocidade da mão do observador.
Qual das fitas representa, no intervalo de tempo considerado (10 tiques), o movimento que tem velocidade escalar média maior?
a) I
b) II
c) III
d) IV
e) V
03. (FUND. CARLOS CHAGAS) Um trem de 200m de comprimento, com velocidade escalar constante de 60 km/h, gasta 36s para atravessar completamente uma ponte. A extensão da ponte, em metros, é de:
a) 200
b) 400
c) 500
d) 600
e) 800
Para as questões 04 e 05
Dois pontos materiais A e B caminham sobre uma mesma reta e no mesmo sentido. na origem dos tempos a distância entre os pontos é de 5,0 km. A velocidade escalar de A é de 80 km/h e a velocidade escalar de B é de 60 km/h, mantidas constantes.
04. A velocidade escalar de A relativa a B é igual a:
a) zero;
b) 80 km/h;
c) -20 km/h
d) 20 km/h
e) -80 km/h
05. A encontra B:
a) no instante t = 15 h;
b) no instante t = 15 min;
c) no instante t = 1/4 min;
d) nunca
e) n.d.a
Para as questões 06 e 07
Dois pontos materiais A e B caminham sobre uma mesma reta e no mesmo sentido. na origem dos tempos a distância entre os pontos é de 5,0 km. A velocidade escalar de A é de 80 km/h e a velocidade escalar de B é de 60 km/h, mantidas constantes.
06. A função horária que descreve o movimento de B, relativo a A para s em km e t em h, é representada por:
a) s = 5,0 - 20t
b) s = 5,0 + 20 t
c) s = 20t
d) s = -20t
e) n.d.a.
07. A função horária que descreve o movimento de A, relativo a B para s em km e t em h, é representada por:
a) s = -5,0 - 20t
b) s = 5,0 + 20 t
c) s = 20t - 5,0
d) s = -20t
e) n.d.a.
08. Considere dois trens T1 e T2 caminhando em linhas férreas retilíneas e paralelas com velocidades de intensidade V1 = 36 km/h e V2 = 72 km/h, em sentidos opostos. Um observador O1 está no trem T1 e nota que a passagem de T2, diante de sua janela, durou um intervalo de tempo de 10s. O tempo gasto por T2, para passar por um túnel de comprimento 200m, é de:
a) 25s
b) 20s
c) 30s
d) 50s
e) 60s
Para as questões 09 e 10
Considere um movimento cuja posição s, em função do tempo t, está representado no gráfico.
09. A distância percorrida pelo móvel entre os instantes t = 0 e t = 20s, em metros, vale:
a) -40
b) zero
c) 20
d) 40
e) 80
10. O móvel passa pela origem no instante:
a) zero
b) 5,0s
c) 10s
d) 15s
e) 20s
Resolução:
01 - B
02 - A 03 - B
04 - D
05 - B
06 - A 07 - C
08 - A
09 - E
10 - C
Acentuação Gráfica dos Monossílabos
1. MONOSSÍLABO (definição)
Monossílabo é palavra de uma só sílaba. Pode ser átono ou tônico.
a) Átono – É o monossílabo pronunciado tão fracamente na frase que a sua intensidade equivale à de uma sílaba átona. Por isso, não tem autonomia fonética e jamais leva acento gráfico.
Exemplos: de, um, uns, sob, em, sem, dum.
b) Tônico – É o monossílabo cuja intensidade se equipara à de uma sílaba tônica, pois é pronunciado fortemente. Nem todos são acentuados graficamente.
Exemplos: pá, pé, pó, pós, cós, dá-lo, pô-lo, só, sós, nó, nós, trem, bem.
2. MONOSSÍLABOS TÔNICOS ACENTUADOS
Acentuam-se os monossílabos tônicos terminados em:
a) a, as – Pá, pás, Brás, já, lá, má, más; fá-lo-ás, fá-lo-ei, fá-lo-emos, trá-lo-ei, trá-lo-íamos;
b) e, es – Pé, pés, crê, crês, dê, dês, vês, mês; fê-lo, fê-la;
c) o, os – Pó, pós, nó, nós, cós, só, sós, dó, pôs; pô-lo-ás, pô-lo-ei, pô-la-íamos, pô-lo, pô-la.
Acentuação das palavras paroxítonas
1. PAROXÍTONA (definição)
Palavra cuja sílaba tônica é a penúltima.
2. PAROXÍTONAS ACENTUADAS
Levam acento gráfico todos os vocábulos paroxítonos terminados em “um xirus não lei ditongo ps”.
Essa frase mnemônica (fácil de reter na memória) contém todas as terminações das palavras paroxítonas acentuadas: “um”, “x”, “i”, “r”, “us”, “n”, “ão”, “l”, “ei”, “ditongo oral” e “ps”.
Veja, a seguir, as explicações e os exemplos necessários para cada terminação.
a) um, uns – Vale para o singular e para o plural: álbum – álbuns; fórum – fóruns.
b) x – Veja que tórax faz o plural os tórax. Dúplex, tríplex, córtex, xérox, Félix (x = s), fênix (x = s).
c) i – Vale para o singular e para o plural: cáqui – cáquis; táxi – táxis.
d) r – Vale para o singular e para o plural, mas observe: palavras paroxítonas terminadas em “r”, no plural tornam-se proparoxítonas: éter – éteres; revólver – revólveres; hambúrguer – hambúrgueres. Caráter tem plural especial: caracteres.
e) us – Veja que o plural é feito com ajuda do artigo: vírus – os vírus; bônus – os bônus; vênus – as vênus.
f) n – Atenção! Se a palavra paroxítona terminada em “n” fizer o plural em “ens”, a forma plural não será acentuada: hífen – hifens; éden – edens; líquen – liquens; hímen – himens.
Se o plural for feito em “ons”, tanto o plural quanto o singular terão acento gráfico: íon – íons; próton – prótons; nêutron – nêutrons, cátion – cátions.
g) ão – A terminação “ão” vale para o masculino e o feminino, para o singular e o plural: órfão – órfãos; órfã – órfãs; ímã – ímãs; zân-gão – zângãos.
h) l – Vale para o singular e para o plural: réptil – répteis; fóssil – fósseis; jóquei – jóqueis. Veja ainda que répteis e fósseis terminam em ditongo decrescente oral.
i) ei – O encontro vocálico “ei” é ditongo decrescente oral: jóquei – jóqueis; fôreis, amáreis,
j) ditongo – As paroxítonas terminadas em ditongo oral, quer crescente quer decrescente, no singular ou no plural, são sempre acentuadas: água, infância, série, mágoa, nódoa, tábua, sério, rosário.
k) ps – Veja que o plural é feito com a ajuda do artigo: bíceps – os bíceps; tríceps – os tríceps; Quéops.
www.colegioweb.com.br
Monossílabo é palavra de uma só sílaba. Pode ser átono ou tônico.
a) Átono – É o monossílabo pronunciado tão fracamente na frase que a sua intensidade equivale à de uma sílaba átona. Por isso, não tem autonomia fonética e jamais leva acento gráfico.
Exemplos: de, um, uns, sob, em, sem, dum.
b) Tônico – É o monossílabo cuja intensidade se equipara à de uma sílaba tônica, pois é pronunciado fortemente. Nem todos são acentuados graficamente.
Exemplos: pá, pé, pó, pós, cós, dá-lo, pô-lo, só, sós, nó, nós, trem, bem.
2. MONOSSÍLABOS TÔNICOS ACENTUADOS
Acentuam-se os monossílabos tônicos terminados em:
a) a, as – Pá, pás, Brás, já, lá, má, más; fá-lo-ás, fá-lo-ei, fá-lo-emos, trá-lo-ei, trá-lo-íamos;
b) e, es – Pé, pés, crê, crês, dê, dês, vês, mês; fê-lo, fê-la;
c) o, os – Pó, pós, nó, nós, cós, só, sós, dó, pôs; pô-lo-ás, pô-lo-ei, pô-la-íamos, pô-lo, pô-la.
Acentuação das palavras paroxítonas
1. PAROXÍTONA (definição)
Palavra cuja sílaba tônica é a penúltima.
| mesa | tórax | pudica | empresa | hifens |
| série | xérox | sótão | ímã | próton |
| álbum | rubrica | recorde | hífen | prótons |
2. PAROXÍTONAS ACENTUADAS
Levam acento gráfico todos os vocábulos paroxítonos terminados em “um xirus não lei ditongo ps”.
Essa frase mnemônica (fácil de reter na memória) contém todas as terminações das palavras paroxítonas acentuadas: “um”, “x”, “i”, “r”, “us”, “n”, “ão”, “l”, “ei”, “ditongo oral” e “ps”.
Veja, a seguir, as explicações e os exemplos necessários para cada terminação.
a) um, uns – Vale para o singular e para o plural: álbum – álbuns; fórum – fóruns.
b) x – Veja que tórax faz o plural os tórax. Dúplex, tríplex, córtex, xérox, Félix (x = s), fênix (x = s).
c) i – Vale para o singular e para o plural: cáqui – cáquis; táxi – táxis.
d) r – Vale para o singular e para o plural, mas observe: palavras paroxítonas terminadas em “r”, no plural tornam-se proparoxítonas: éter – éteres; revólver – revólveres; hambúrguer – hambúrgueres. Caráter tem plural especial: caracteres.
e) us – Veja que o plural é feito com ajuda do artigo: vírus – os vírus; bônus – os bônus; vênus – as vênus.
f) n – Atenção! Se a palavra paroxítona terminada em “n” fizer o plural em “ens”, a forma plural não será acentuada: hífen – hifens; éden – edens; líquen – liquens; hímen – himens.
Se o plural for feito em “ons”, tanto o plural quanto o singular terão acento gráfico: íon – íons; próton – prótons; nêutron – nêutrons, cátion – cátions.
g) ão – A terminação “ão” vale para o masculino e o feminino, para o singular e o plural: órfão – órfãos; órfã – órfãs; ímã – ímãs; zân-gão – zângãos.
h) l – Vale para o singular e para o plural: réptil – répteis; fóssil – fósseis; jóquei – jóqueis. Veja ainda que répteis e fósseis terminam em ditongo decrescente oral.
i) ei – O encontro vocálico “ei” é ditongo decrescente oral: jóquei – jóqueis; fôreis, amáreis,
j) ditongo – As paroxítonas terminadas em ditongo oral, quer crescente quer decrescente, no singular ou no plural, são sempre acentuadas: água, infância, série, mágoa, nódoa, tábua, sério, rosário.
k) ps – Veja que o plural é feito com a ajuda do artigo: bíceps – os bíceps; tríceps – os tríceps; Quéops.
www.colegioweb.com.br
Aplicações da Função do 2º grau na Física
A função do 2º grau está presente em inúmeras situações cotidianas, na Física ela possui um papel importante na análise dos movimentos uniformemente variados (MUV), pois em razão da aceleração, os corpos variam a velocidade e o espaço em função do tempo.
Uma função do 2º grau obedece à seguinte lei de formação f(x) = ax2 + bx + c,
na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão S = S0 + V0t + (at2)/2, onde
a: aceleração, S: espaço, V: velocidade e t: tempo.
Exemplo 1
Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?
Resolução:
A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:
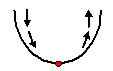
Devemos calcular o ponto mínimo da parábola, dado por:
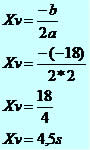
Exemplo 2
Um canhão atira um projétil (figura), descrevendo a função s = -9t2 + 120t, sendo s em metros e t em segundos. Calcule o ponto máximo de altura atingida pelo projétil.
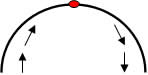
Resolução:
A função do movimento do projétil descreve uma parábola decrescente (a < 0), o ponto máximo da parábola será a altura máxima atingida pelo projétil.
Ponto máximo
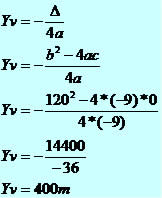
mundoeducacao
Uma função do 2º grau obedece à seguinte lei de formação f(x) = ax2 + bx + c,
na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão S = S0 + V0t + (at2)/2, onde
a: aceleração, S: espaço, V: velocidade e t: tempo.
Exemplo 1
Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?
Resolução:
A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:
Devemos calcular o ponto mínimo da parábola, dado por:
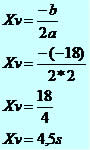
Exemplo 2
Um canhão atira um projétil (figura), descrevendo a função s = -9t2 + 120t, sendo s em metros e t em segundos. Calcule o ponto máximo de altura atingida pelo projétil.
Resolução:
A função do movimento do projétil descreve uma parábola decrescente (a < 0), o ponto máximo da parábola será a altura máxima atingida pelo projétil.
Ponto máximo
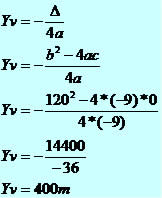
mundoeducacao
Calculo da matriz inversa por meio de determinantes
A determinação de uma matriz inversa de ordem n é dada através da multiplicação por uma matriz B genérica, sendo que o resultado deverá ser uma matriz identidade. Lembrando que matriz identidade de ordem n é uma matriz onde a diagonal principal é preenchida pelo número 1 e os demais espaços são preenchidos com o número 0.
Exemplos de uma Matriz Identidade:
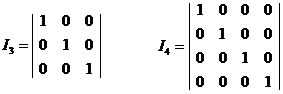
Exemplos de uma Matriz Identidade:
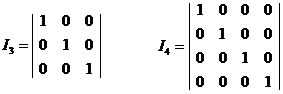
A matriz B será representada por uma matriz genérica de mesmo número de colunas e linhas.
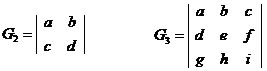
Exemplo 1
Vamos determinar, se existir, a inversa da matriz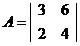
.
Vamos determinar, se existir, a inversa da matriz
.
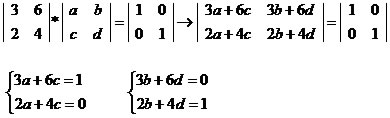
Os sistemas não possuem resolução, são impossíveis. Nesse tipo de situação, onde os sistemas não podem ser solucionados, chegamos à conclusão que a matriz A não possui inversa.
Exemplo 2
Determine, se existir, a inversa da matriz
.
Exemplo 2
Determine, se existir, a inversa da matriz
.
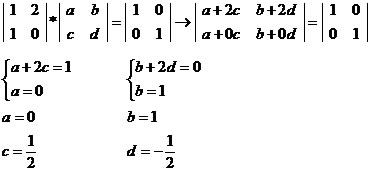
a + 2c = 1
a = 0
b + 2d = 0
b = 1
Portanto, a matriz inversa de
é 
.www.mundoeducacao.com.br
Teoria dos conjuntos
Colégio Estadual Dinah Gonçalves
email accbarroso@hotmail.com
Relação de pertinência
Cada aluno da classe tem uma mesma propriedade: estar na sala de aula. Assim, ao falarmos neste conjunto estabelecemos a possibilidade de averiguar se uma pessoa pertence ou não a ele. O conceito básico da teoria dos conjuntos é a relação de pertinência representada pelo símbolo Î. As letras minúsculas designam os elementos de um conjunto e as maiúsculas, os conjuntos. Assim, o conjunto das vogais (V) é: V = {a, e, i, o, u}
→ A relação de pertinência é expressa por: a Î V, pois o elemento a pertence ao conjunto V.
→ A relação de não-pertinência é expressa por: b Î V, pois o elemento b não pertence ao conjunto V.
Formação de um conjunto
Um conjunto pode ser definido de duas maneiras:
→ Enumerando todos os elementos do conjunto: S = {1, 3, 5, 7, 9}
→ Expressando uma ou mais propriedades que se verificam para todos os seus elementos e somente para eles:
S = {números ímpares de um algarismo} Podemos representá-lo assim:
B = {x Î S / x tem a propriedade P}; (lê-se: x pertence ao conjunto S tal que x possui a propriedade P).
O conjunto B é formado por todos os elementos de S que possuem a propriedade P.
Exemplo: B = {x Î IN / x < 8} = {0, 1, 2, 3, 4, 5, 6, 7}
Conjunto vazio: Ø ou { }
É aquele que não contém nenhum elemento.
Subconjuntos de um conjunto
Quando todos os elementos de um conjunto A pertencem também a outro conjunto B, dizemos que:
A é um subconjunto de B, ou então que ... A é uma parte de B, ou então que ... A está incluído em B e escrevemos A Î B.
Se existir pelo menos um elemento de A que não pertença a B, diremos então que A não está incluído em B e escreveremos A Ë B.
Conjunto das partes de um conjunto
Se tivermos um conjunto de elementos a que chamamos F, o conjunto das partes de F será aquele formado por todos os possíveis subconjuntos de F e será representado por P(F).
Se o conjunto F tem n elementos, então o conjunto das partes de F, P(F), terá 2n elementos.
Exemplo: Sendo F = {3, 5, 9}, vamos escrever todos os possíveis subconjuntos de F:
→ com nenhum elemento Ø
→ com 1 elemento {3}, {5}, {9}
→ com 2 elementos {3, 5}, {3, 9}, {5, 9}
→ com 3 elementos {3, 5, 9}
Podemos então escrever: P(F) = { Ø, {3}, {5}, {9}, {3, 5}, {3, 9}, {5, 9}, {3, 5, 9} }
O número de elementos de um conjunto F é denominado ordem do conjunto e é indicado por n(F).
Repare que no exemplo acima n(F) = 3 e n (P(F)) = 23 = 8
Relação de inclusão
A relação de inclusão possui 3 propriedades:
→ Propriedade reflexiva: A Î A, isto é, um conjunto sempre é subconjunto dele mesmo.
→ Propriedade anti-simétrica: se A Î B e B Î A, então A = B.
→ Propriedade transitiva: se A Î B e B Î C, então A Î C.
Conjunto complementar
Complementar de A com respeito a R e é representada por CRA = R - A.
No caso dos alunos de uma classe, o conjunto complementar do conjunto dos alunos presentes à aula será formado pelos alunos ausentes à aula.
União e intersecção de conjuntos
Dados dois conjuntos A e B, existe sempre um terceiro formado pelos elementos que pertencem a pelo menos um dos conjuntos a que chamamos conjunto união e representamos por: A U B.
Formalmente temos que: A U B = {x / x Î A ou x Î B}
A união de conjuntos obedece às seguintes propriedades:
→ Propriedade comutativa: A U B = B U A
→ Propriedade associativa: A U (B U C) = (A U B) U C
→ Elemento Neutro: A U Ø = A
Utilizando os diagramas de Venn (Figura abaixo), verificamos algumas das propriedades acima.
A intersecção dos conjuntos A e B é o conjunto formado pelos elementos que são ao mesmo tempo de A e de B, e é representada por: A ∩ B
Formalmente temos que: A ∩ B = {x| xÎA e xÎB}
A intersecção dos conjuntos A e B é o conjunto formado pelos elementos que são ao mesmo tempo de A e de B, e é representada por: A ∩ B
Formalmente temos que: A ∩ B = {x| xÎA e xÎB}
A intersecção de dois conjuntos obedece às seguintes propriedades:
→ Propriedade comutativa: A ∩ B = B ∩ A
→ Propriedade associativa: A ∩ (B∩C) = (A∩B) ∩ C
→ Propriedade de idempotência: A ∩ A = A
→ A ∩ Ø = Ø
Relacionando união e intersecção, surgem duas outras propriedades interessantes:
→ Propriedade distributiva da união com relação à intersecção: A U (B∩C) = (AUB) ∩ (AUC);
→ Propriedade distributiva da intersecção com relação à união: A ∩ (BUC) = (A∩B) U (A∩C).
Produto cartesiano
O produto cartesiano de dois conjuntos A e B, escrito A x B, é o conjunto formado por todos os pares ordenados (a, b), em que o primeiro elemento a pertence a A e o segundo elemento b pertence a B.
Simbolicamente, podemos escrever:
A X B = {(a, b)| a Î A, b Î B}
Se A = {1, 2} e B = {x, y, z}, então: A X B = {(1, x), (1, y), (1, z), (2, x), (2, y), (2, z)}
O conjunto A x B tem 2 x 3 = 6 elementos.
Em geral, se A tem a elementos e B tem b elementos, A x B tem a x b elementos, isto é:
se n(A) = a e n(B) = b, temos que n(A x B) = a x b.
É importante salientar que os pares ordenados recebem estes nomes por se constituírem de 2 elementos em que é fundamental a ordem na qual se apresentam.
No exemplo, o par (1, x) pertence a A x B. Mas o mesmo não acontece com o par (x, 1), que pertenceria ao produto B x A.
É por isso que se afirma que o produto cartesiano não tem a propriedade comutativa. Ele pode ser representado de várias formas:
→ Com um diagrama de flechas.
→ Com um diagrama cartesiano.
→ Com um diagrama em árvore.
As propriedades do produto cartesiano são as seguintes:
→ Propriedade associativa: (A x B) x C = A x (B x C) = A x B x C
→ A x Ø = Ø
→ A x B = Ø se, e somente se, A = Ø ou B = Ø
→ Se C ≠ Ø e A x C = B x C, então: A = B
Os conjuntos numéricos
A expansão contínua do campo numérico chegou, no final do século XIX, de forma totalmente desordenada. Os matemáticos estruturaram, então, uma teoria de conjuntos numéricos que, de certa forma, seguiu a lógica do processo histórico de criação do número.
O conjunto dos números naturais IN
O mais simples. Por ser um conjunto discreto, pode ter uma representação explícita:
IN = {0, 1, 2, 3, 4, 5...}
IN = {0, 1, 2, 3, 4, 5...}
O conjunto dos números inteiros Z
É o que resulta da expansão de IN na integração dos números negativos. Por ser um conjunto discreto, pode ter representação explícita: Z = {... -3, -2, -1, 0, 1, 2, 3,...}.
O conjunto dos números racionais Q
É a expansão do conjunto Z, na qual o campo numérico passa a ocupar a parte racional da continuidade.
Por não ocupá-la completamente, é considerado um conjunto denso, sem representação explícita. Pode existir na reta, desde que se indiquem os espaços vazios da descontinuidade, que correspondem aos números irracionais, também à esquerda de zero.
O conjunto dos números reais IR
É a expansão do conjunto Q na qual o campo numérico passa a ocupar toda a continuidade, graças à união dos campos racional e irracional. Por se tratar de um conjunto contínuo, não tem representação explícita. É um conjunto numérico que ocupa todos os pontos da reta, também à esquerda de zero.
fonte:matematiques.com.br
Operações com conjuntos
Operações envolvendo conjuntos
1. União de conjuntos.
Dados dois conjuntos A e B, a união de A com B é o conjunto formado pelos elementos que pertencem ao conjunto A ou ao conjunto B.
Exemplo: Considerando os conjuntos A = {1, 3, 5, 7, 9, 11} e B = {8, 9, 10, 11, 12}, temos que:
A U B = {1, 3, 5, 7, 8, 9, 10, 11, 12}
2. Intersecção de conjuntos.
Dados dois conjuntos A e B, a intersecção de A com B é o conjunto formado pelos elementos que pertencem ao conjunto A e ao conjunto B. De uma forma mais simples, é o conjunto formado pelos elementos que são comuns aos dois conjuntos.
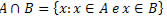
Exemplo 1: Seja A = {1, 3, 5, 7, 9, 11} e B = {8, 9, 10, 11, 12}, temos que:
A ∩ B = {9, 11}
Exemplo 2. A = {1, 3, 5, 7, 9, 11} e C = {2, 4, 6, 8, 10}
A ∩ C = ø, pois os dois conjuntos não apresentam elementos em comum.
A operação de intersecção apresenta algumas propriedades:
a) Propriedade reflexiva.
A ∩ A = A
b) Propriedade comutativa.
A ∩ B = B ∩ A
c) Propriedade associativa.
A ∩ (B ∩ C) = (A ∩ B) ∩ C
d) Propriedade distributiva.
A ∩ (B U C) = (A ∩ B) U (A ∩ C)
A U (B ∩ C) = (A U B) ∩ (A U C)
Graficamente, utilizando os diagramas de Venn, podemos representar a operação de intersecção da seguinte forma:
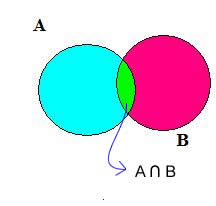
Dados dois conjuntos A e B, a diferença entre A e B é o conjunto formado pelos elementos de A que não pertencem a B.
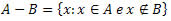
Exemplo: A = {1, 3, 5, 7, 9, 11} e B = {8, 9, 10, 11, 12}
A – B = {1, 3, 5, 7}
B – A = {8, 10, 12}
4. Complementar de um conjunto.
Essa operação é um caso particular de diferença entre conjuntos. Considere dois conjuntos, A e B, sendo que B está contido em A
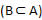, ou seja, B é um subconjunto de A. O complementar de B em relação a A, representado por CAB, é a diferença A – B.Exemplo: Sejam A = {2, 4, 6, 8, 10, 12, 14} e B = {4, 8, 12}, temos que:
CAB = A – B = {2, 6, 10, 14}
Marcelo Rigonatto
Conjunto
Pertencem ao conjunto dos naturais os números inteiros positivos incluindo o zero. Representado pela letra N maiúscula. Os elementos dos conjuntos devem estar sempre entre chaves.
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... }
♦ Quando for representar o Conjunto dos Naturais não – nulos (excluindo o zero) devemos colocar * ao lado do N.
Representado assim:
N* = {1, 2,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12, ... }
A reticência indica que sempre é possível acrescentar mais um elemento.
N = {0, 1, 2, 3, 4, 5, 6, ...} ou N = {0, 1, 2, 3, 4, 5, 6, 7, ... }
Qualquer que seja o elemento de N, ele sempre tem um sucessor. Também falamos em antecessor de um número.
• 6 é o sucessor de 5.
• 7 é o sucessor de 6.
• 19 é antecessor de 20.
• 47 é o antecessor de 48.
Como todo número natural tem um sucessor, dizemos que o conjunto N é infinito.
Quando um conjunto é finito?
O conjunto dos números naturais maiores que 5 é infinito: {6, 7, 8, 9, ...}
Já o conjunto dos números naturais menores que 5 é finito: {0, 1, 2, 3, 4}
Veja mais alguns exemplos de conjuntos finitos.
• O conjunto dos alunos da classe.
• O conjunto dos professores da escola.
• O conjunto das pessoas que formam a população brasileira.
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... }
♦ Quando for representar o Conjunto dos Naturais não – nulos (excluindo o zero) devemos colocar * ao lado do N.
Representado assim:
N* = {1, 2,3 ,4 ,5 ,6 ,7 ,8 ,9 ,10 ,11 ,12, ... }
A reticência indica que sempre é possível acrescentar mais um elemento.
N = {0, 1, 2, 3, 4, 5, 6, ...} ou N = {0, 1, 2, 3, 4, 5, 6, 7, ... }
Qualquer que seja o elemento de N, ele sempre tem um sucessor. Também falamos em antecessor de um número.
• 6 é o sucessor de 5.
• 7 é o sucessor de 6.
• 19 é antecessor de 20.
• 47 é o antecessor de 48.
Como todo número natural tem um sucessor, dizemos que o conjunto N é infinito.
Quando um conjunto é finito?
O conjunto dos números naturais maiores que 5 é infinito: {6, 7, 8, 9, ...}
Já o conjunto dos números naturais menores que 5 é finito: {0, 1, 2, 3, 4}
Veja mais alguns exemplos de conjuntos finitos.
• O conjunto dos alunos da classe.
• O conjunto dos professores da escola.
• O conjunto das pessoas que formam a população brasileira.
Ciclo da cana-de-acúcar
Introdução:
O ciclo da cana-de-açúcar foi a primeira atividade economicamente organizada do Brasil. A partir da fundação do primeiro engenho de cana-de-açúcar pelo Sr Martins Afonso de Souza, em 1532, e por mais de dois séculos o açúcar foi o principal produto brasileiro, convivendo, contribuindo e, às vezes, resistindo às mudanças sócio-politico-culturais deste período.
Este estudo visa resgatar o período de reinado do açúcar, enquanto “embaixador” do Brasil, colônia portuguesa recém descoberta e sem maior expressividade ou mesmo importância econômica, na Europa dos séculos XVI a XIX.
Serão enfocados, neste trabalho, características como motivo, facilitadores, dificultadores, pressões, conflitos e conseqüências decorrentes do ciclo da cana-de-açúcar.
A necessidade de colonizar a terra para defendê-la e explorar suas riquezas fizeram com que o Governo de Portugal instalasse engenhos produtores de açúcar no nosso litoral, essa cultura foi escolhida por se tratar de um produto de alto valor no comércio europeu e por seu consumo crescente na Europa.
Logo, após as dificuldades de sua implantação - a falta de dinheiro para montar a moenda, comprar escravos, refinar o açúcar e sobretudo transportá-lo nos mercados consumidores da Europa - o açúcar tornou-se o principal produto brasileiro e foi a base de sustentação da economia e da colonização do Brasil durante os século XVI e XVII.
Já no século XVIII o surgimento do açúcar de beterraba e a formação dos conhecimentos e técnicas para construção de uma indústria açucareira por parte dos holandeses fizeram com que nosso principal produto entrasse em decadência e perdesse mercado consumidor na Europa. Assim, acabaria o monopólio do açúcar e alteraria o quadro político-econômico da época em nosso país.
Surgimento da Economia Açucareira:
No início da colonização Brasileira o governo metropolitano resolveu estimular alguns portugueses a instalarem engenhos para produzirem açúcar no litoral do Brasil. Era preciso efetivar a aposse da terra para defendê-la e também explorá-la em suas riquezas. Optou-se pela cana de açúcar por se tratar de uma cultura rápida, chegando ao corte a partir do segundo ano e também devido ao tipo de solo existente, o massapé excelente para o plantio de cana. Além disso o Nordeste, por sua localização estratégica, permitia fácil escoamento do açúcar produzido estando mais próximo dos mercados consumidores. Outro fator que contribuiu na decisão de cultivar a cana, foi o preço do açúcar alcançado no comércio europeu.
O consumo do açúcar , em ascendência na Europa, logo seria o principal produto Brasileiro - séculos XVI e XVII - tornando o açúcar a base de sustentação da economia e da colonização do Brasil durante estes períodos.
A utilização do açúcar como adoçante, em substituição ao mel, causou na Europa do século XVI uma revolução comportamental e comercial uma vez que o produto era usado anteriormente apenas como remédio. Esse Fato destacou o Brasil, como grande produtor de açúcar, no mercado europeu.
A cultura da cana de açúcar propiciava aos donatários de terras da ocupação das mesmas pois povoados se formavam em torno dos engenhos. O primeiro engenho foi instalado por Martins Afonso de Souza, em 1532.
Foram grandes as dificuldade encontradas para desenvolver o ciclo do açúcar, tais como: dinheiro para montar as moendas, comprar escravos, transportar os colonos brancos, comprar navios para transportar os equipamentos e sustentar os trabalhadores até que a produção do açúcar desse lucro, além da preocupação com o refino e comercialização do produto.
Os holandeses surgem, então, como financiadores, transportadores e negociadores do nosso açúcar no mercado consumidor europeu. Podemos dizer que foram os holandeses o maiores beneficiados de forma lucrativa com o nosso açúcar.
A produção do açúcar no brasil se tornou motivo de grandes invasões, como as holandesas ocorrida em Pernambuco, maior produtor de açúcar. Estas invasões resultaram em grande perda de engenhos, muitos destruídos, causando um retrocesso na economia, que logo se recuperou pois o declínio da mineração, no final do de século XVII, permitiu um novo florescimento da economia açucareira, não só em Pernambuco, e na Bahia onde era tradicional, mas também na região de Campos e em algumas zonas de São Paulo. Essa economia teve como classe dominante os grandes proprietários senhores de engenho, que eram também os donos de escravos (classe dominada) e os donos do poder.
Desenvolvimento da Economia Açucareira:
Os centros urbanos que se desenvolveram em áreas especializadas na cultura da cana e no fabrico do açúcar foram, no Brasil, os pontos que se tornaram os mais desenvolvidos em valores da nossa cultura moral, intelectual, religiosa, científica e artística.
Em 1560, Portugal ganhava ascendência no comércio europeu, com o açúcar fabricado no Brasil. Com o êxito do açúcar no comércio, o governo português incentivou a expansão das fábricas em sua colônia tropical americana. Com isso Portugal estava, com estímulos oficiais, desenvolvendo a economia brasileira. Lavoura extensivas de cana-de-açúcar surgiram para alimentar os engenhos. Estes por sua vez eram instalados à beira-mar ou nas proximidades dos rios por necessidade não só de seu funcionamento como também pela questão de transporte do produto. Ao lado do canavial, nascia a agricultura de subsistência, para atender a crescente necessidade de alimentos para a casa grande, a senzala e a pequena parcela de assalariados livres. A propriedade rural, verdadeiro feudo, era, então, assim formada:
A casa-grande onde vivia o senhor com sua família, exercendo grande autoridade sobre todos. Era um verdadeiro patriarca.
A senzala era uma grande construção onde os negros escravos viviam miseravelmente, tratados como animais e sujeitos a toda a sorte de violência e castigos.
A capela onde se realizavam as cerimônias religiosas. Além, de centro religioso, a capela era um centro social, pois nela se reuniam todos os homens livres do engenho e das proximidades.
E a moenda, onde a cana-de-açúcar era moída. O caldo corria da moenda para os tachos por meio de calhas. Dos tachos, o caldo era retirado em vasilhas de cobre e levado para a caldeira, onde era fervido e mexido pelos escravos, que tiravam as impurezas e a espuma.
O rápido desenvolvimento da indústria açucareira, fez com que o governo português não se limitasse só a fabrica de moenda e engenho de água, mais numa busca rápida desta lavoura, graças à uma abundante mão-de-obra indígena existente já nas colônias deste século ligada a essa atividade. O começo da colonização se deu em pequenas comunidades que teve importante papel na especialização de mão-de-obra dos escravos. Logo depois veio a mão-de-obra dos escravos africano, que chegou para a expansão da empresa, quando os lucros já se encontravam assegurados. Era um sistema de produção rentável e capitalizado.
Durante o ciclo do açúcar ocorreu a ocupação Holandesa no Brasil. Desde o início do ciclo do açúcar, notava-se o interesse comum entre portugueses e flamengos. Logo após a ocupação holandesa em 1580, os flamengos começaram a trabalhar em Pernambuco registrando-se uma exportação de 512.273 arrobas de açúcar branco, mascavo e “de panela”. Foram também os Holandeses que trouxeram as moedas metálicas para o Brasil.
Durante o domínio holandês foi estimulada a imigração, para Pernambuco e capitanias vizinhas, de europeus qualificados como senhores de engenho ou agricultores, entre eles muitos judeus ricos, oriundos da Holanda, da Alemanha, da Hungria e da Polônia, os quais também adquiriram seus engenhos.
Quando Portugal conseguiu finalmente expulsar os flamengos, que haviam passado a dominar o processo de fabricação do açúcar, estes foram para as Antilhas e lá desenvolveram a produção do açúcar. Assim, Brasil e Antilhas assumiram, durante os séculos XVII e XVIII, o papel de abastecedores de açúcar para o mercado europeu.
Desarticulação da Economia Açucareira:
Quando Portugal foi absorvido pela Espanha modificou-se profundamente o quadro político-econômico do Brasil, surgindo o interesse da Holanda em controlar o comércio do açúcar. Desse interesse surge uma guerra sem quartel contra a Espanha. Como efeito dessa guerra temos o controle, por parte dos holandeses, do transporte e comercialização de açúcar na Europa do século XVII.
Do século XVIII ao XIX o açúcar continuou a ter importância na economia do nosso país, embora o café viesse a se tornar o principal produto brasileiro. Mas pouco a pouco o açúcar perdeu mercado e foi deixando de ser a base de sustentação da nossa economia.
Outros acontecimentos que prejudicaram o açúcar brasileiro foram o Bloqueio de Napoleão Bonaparte contra os navios ingleses transportadores de açúcar do nosso continente para o mercado consumidor europeu e o aparecimento do açúcar de beterraba, o chamado “açúcar alemão”. Esse novo produto foi utilizado pelos países consumidores como um produto substituto ao açúcar da cana, ocorrendo o agravamento da crise do nosso açúcar e os maus efeitos decorrentes da monocultura latifundiária em nossa economia.
Com todos esses problemas e com o descaso do Governo de Portugal em relação a sua colônia ocorreu a desarticulação da economia açucareira no Brasil, isso tendo como forte aliado: o preconceito em relação ao clima e a relação de inferioridade do nosso povo. Em suma, alimentávamos, em relação a nós próprios, praticamente todos os preconceitos e aprendemos a valorizar e admirar o alheio, o que é estrangeiro, e menosprezar o que é nosso, chegando a ter vergonha de nós mesmos.
Encerramento da Economia Açucareira:
A guerra realizada pela Holanda contra a Espanha modificou a nossa colonização, os grandes beneficiados foram os holandeses que passaram a ter praticamente todo o comércio dos países europeus realizado por mar, pois, era o meio de transporte mais rápido e importante da época. Sendo que, no Brasil, os batavos detiveram o controle da produção do açúcar, sendo um grande modificador para nossa economia.
Os holandeses, enquanto estiveram no Brasil, adquiriram todo o conhecimento de técnicas e organizações da indústria açucareira, pois, era isso o que eles precisavam para implantarem uma nova base industrial. A partir desse momento, estaria perdido o monopólio e alterado os dois grupos representativos da época, os portugueses produtores e os holandeses financiadores.
Assim, a partir de meados do século XVIII e durante todo o século XIX, o preço do açúcar permaneceu reduzido à metade. Sem recursos próprios para conter a desvalorização do açúcar o Governo de Portugal e os produtores portugueses mudam atenção para o café, no século XIX.
Dessa forma houve no próprio funcionamento do ciclo do açúcar, elementos negativos que impediram sua viabilidade ao progresso. Ocorrendo, então, o encerramento do monopólio da economia açucareira que manteve sua importância, porém deixou de ser o principal produto e a base de sustentação da economia brasileira.
A essa altura já se ia encerrando o ciclo do açúcar tendo como conseqüência o êxodo da população para a região de mineração no interior do Brasil.
Conclusão:
A cultura do açúcar surgiu, no Brasil, pela necessidade de colonizar a terra, para defendê-la e para explorar suas riquezas.
A importância dessa cultura pode ser exemplificada pelo interesse dos holandeses, que atravessaram mares para invadir Pernambuco, à época maior produtor de açúcar. Mesmo quando expulsos, os holandeses não abandoaram a produção de açúcar. Optaram pela transferência do know how do cultivo da cana e refino do produto para as Antilhas que, ao lado do Brasil, dominaram o comércio de açúcar na Europa nos séculos XVII e XVIII.
Embora essa cultura tenha sido responsável pela base de sustentação da economia e da colonização do nosso país durante os século XVI e XVII, o governo português não assegurou à sua colônia condições para manutenção do monopólio sobre seu domínio, que primeiro passa aos holandeses e posteriormente é compartilhado com os mesmos.
Também contribui para o declínio do produto a perda de importância do mesmo no mercado europeu em decorrência ao surgimento do açúcar de beterraba.
Assim, no século XIX, o açúcar deixa de ser principal produto nacional papel que passa, então, a ser exercido pelo café.
Autoria: Fabíola Schwartz
O ciclo da cana-de-açúcar foi a primeira atividade economicamente organizada do Brasil. A partir da fundação do primeiro engenho de cana-de-açúcar pelo Sr Martins Afonso de Souza, em 1532, e por mais de dois séculos o açúcar foi o principal produto brasileiro, convivendo, contribuindo e, às vezes, resistindo às mudanças sócio-politico-culturais deste período.
Este estudo visa resgatar o período de reinado do açúcar, enquanto “embaixador” do Brasil, colônia portuguesa recém descoberta e sem maior expressividade ou mesmo importância econômica, na Europa dos séculos XVI a XIX.
Serão enfocados, neste trabalho, características como motivo, facilitadores, dificultadores, pressões, conflitos e conseqüências decorrentes do ciclo da cana-de-açúcar.
A necessidade de colonizar a terra para defendê-la e explorar suas riquezas fizeram com que o Governo de Portugal instalasse engenhos produtores de açúcar no nosso litoral, essa cultura foi escolhida por se tratar de um produto de alto valor no comércio europeu e por seu consumo crescente na Europa.
Logo, após as dificuldades de sua implantação - a falta de dinheiro para montar a moenda, comprar escravos, refinar o açúcar e sobretudo transportá-lo nos mercados consumidores da Europa - o açúcar tornou-se o principal produto brasileiro e foi a base de sustentação da economia e da colonização do Brasil durante os século XVI e XVII.
Já no século XVIII o surgimento do açúcar de beterraba e a formação dos conhecimentos e técnicas para construção de uma indústria açucareira por parte dos holandeses fizeram com que nosso principal produto entrasse em decadência e perdesse mercado consumidor na Europa. Assim, acabaria o monopólio do açúcar e alteraria o quadro político-econômico da época em nosso país.
Surgimento da Economia Açucareira:
No início da colonização Brasileira o governo metropolitano resolveu estimular alguns portugueses a instalarem engenhos para produzirem açúcar no litoral do Brasil. Era preciso efetivar a aposse da terra para defendê-la e também explorá-la em suas riquezas. Optou-se pela cana de açúcar por se tratar de uma cultura rápida, chegando ao corte a partir do segundo ano e também devido ao tipo de solo existente, o massapé excelente para o plantio de cana. Além disso o Nordeste, por sua localização estratégica, permitia fácil escoamento do açúcar produzido estando mais próximo dos mercados consumidores. Outro fator que contribuiu na decisão de cultivar a cana, foi o preço do açúcar alcançado no comércio europeu.
O consumo do açúcar , em ascendência na Europa, logo seria o principal produto Brasileiro - séculos XVI e XVII - tornando o açúcar a base de sustentação da economia e da colonização do Brasil durante estes períodos.
A utilização do açúcar como adoçante, em substituição ao mel, causou na Europa do século XVI uma revolução comportamental e comercial uma vez que o produto era usado anteriormente apenas como remédio. Esse Fato destacou o Brasil, como grande produtor de açúcar, no mercado europeu.
A cultura da cana de açúcar propiciava aos donatários de terras da ocupação das mesmas pois povoados se formavam em torno dos engenhos. O primeiro engenho foi instalado por Martins Afonso de Souza, em 1532.
Foram grandes as dificuldade encontradas para desenvolver o ciclo do açúcar, tais como: dinheiro para montar as moendas, comprar escravos, transportar os colonos brancos, comprar navios para transportar os equipamentos e sustentar os trabalhadores até que a produção do açúcar desse lucro, além da preocupação com o refino e comercialização do produto.
Os holandeses surgem, então, como financiadores, transportadores e negociadores do nosso açúcar no mercado consumidor europeu. Podemos dizer que foram os holandeses o maiores beneficiados de forma lucrativa com o nosso açúcar.
A produção do açúcar no brasil se tornou motivo de grandes invasões, como as holandesas ocorrida em Pernambuco, maior produtor de açúcar. Estas invasões resultaram em grande perda de engenhos, muitos destruídos, causando um retrocesso na economia, que logo se recuperou pois o declínio da mineração, no final do de século XVII, permitiu um novo florescimento da economia açucareira, não só em Pernambuco, e na Bahia onde era tradicional, mas também na região de Campos e em algumas zonas de São Paulo. Essa economia teve como classe dominante os grandes proprietários senhores de engenho, que eram também os donos de escravos (classe dominada) e os donos do poder.
Desenvolvimento da Economia Açucareira:
Os centros urbanos que se desenvolveram em áreas especializadas na cultura da cana e no fabrico do açúcar foram, no Brasil, os pontos que se tornaram os mais desenvolvidos em valores da nossa cultura moral, intelectual, religiosa, científica e artística.
Em 1560, Portugal ganhava ascendência no comércio europeu, com o açúcar fabricado no Brasil. Com o êxito do açúcar no comércio, o governo português incentivou a expansão das fábricas em sua colônia tropical americana. Com isso Portugal estava, com estímulos oficiais, desenvolvendo a economia brasileira. Lavoura extensivas de cana-de-açúcar surgiram para alimentar os engenhos. Estes por sua vez eram instalados à beira-mar ou nas proximidades dos rios por necessidade não só de seu funcionamento como também pela questão de transporte do produto. Ao lado do canavial, nascia a agricultura de subsistência, para atender a crescente necessidade de alimentos para a casa grande, a senzala e a pequena parcela de assalariados livres. A propriedade rural, verdadeiro feudo, era, então, assim formada:
A casa-grande onde vivia o senhor com sua família, exercendo grande autoridade sobre todos. Era um verdadeiro patriarca.
A senzala era uma grande construção onde os negros escravos viviam miseravelmente, tratados como animais e sujeitos a toda a sorte de violência e castigos.
A capela onde se realizavam as cerimônias religiosas. Além, de centro religioso, a capela era um centro social, pois nela se reuniam todos os homens livres do engenho e das proximidades.
E a moenda, onde a cana-de-açúcar era moída. O caldo corria da moenda para os tachos por meio de calhas. Dos tachos, o caldo era retirado em vasilhas de cobre e levado para a caldeira, onde era fervido e mexido pelos escravos, que tiravam as impurezas e a espuma.
O rápido desenvolvimento da indústria açucareira, fez com que o governo português não se limitasse só a fabrica de moenda e engenho de água, mais numa busca rápida desta lavoura, graças à uma abundante mão-de-obra indígena existente já nas colônias deste século ligada a essa atividade. O começo da colonização se deu em pequenas comunidades que teve importante papel na especialização de mão-de-obra dos escravos. Logo depois veio a mão-de-obra dos escravos africano, que chegou para a expansão da empresa, quando os lucros já se encontravam assegurados. Era um sistema de produção rentável e capitalizado.
Durante o ciclo do açúcar ocorreu a ocupação Holandesa no Brasil. Desde o início do ciclo do açúcar, notava-se o interesse comum entre portugueses e flamengos. Logo após a ocupação holandesa em 1580, os flamengos começaram a trabalhar em Pernambuco registrando-se uma exportação de 512.273 arrobas de açúcar branco, mascavo e “de panela”. Foram também os Holandeses que trouxeram as moedas metálicas para o Brasil.
Durante o domínio holandês foi estimulada a imigração, para Pernambuco e capitanias vizinhas, de europeus qualificados como senhores de engenho ou agricultores, entre eles muitos judeus ricos, oriundos da Holanda, da Alemanha, da Hungria e da Polônia, os quais também adquiriram seus engenhos.
Quando Portugal conseguiu finalmente expulsar os flamengos, que haviam passado a dominar o processo de fabricação do açúcar, estes foram para as Antilhas e lá desenvolveram a produção do açúcar. Assim, Brasil e Antilhas assumiram, durante os séculos XVII e XVIII, o papel de abastecedores de açúcar para o mercado europeu.
Desarticulação da Economia Açucareira:
Quando Portugal foi absorvido pela Espanha modificou-se profundamente o quadro político-econômico do Brasil, surgindo o interesse da Holanda em controlar o comércio do açúcar. Desse interesse surge uma guerra sem quartel contra a Espanha. Como efeito dessa guerra temos o controle, por parte dos holandeses, do transporte e comercialização de açúcar na Europa do século XVII.
Do século XVIII ao XIX o açúcar continuou a ter importância na economia do nosso país, embora o café viesse a se tornar o principal produto brasileiro. Mas pouco a pouco o açúcar perdeu mercado e foi deixando de ser a base de sustentação da nossa economia.
Outros acontecimentos que prejudicaram o açúcar brasileiro foram o Bloqueio de Napoleão Bonaparte contra os navios ingleses transportadores de açúcar do nosso continente para o mercado consumidor europeu e o aparecimento do açúcar de beterraba, o chamado “açúcar alemão”. Esse novo produto foi utilizado pelos países consumidores como um produto substituto ao açúcar da cana, ocorrendo o agravamento da crise do nosso açúcar e os maus efeitos decorrentes da monocultura latifundiária em nossa economia.
Com todos esses problemas e com o descaso do Governo de Portugal em relação a sua colônia ocorreu a desarticulação da economia açucareira no Brasil, isso tendo como forte aliado: o preconceito em relação ao clima e a relação de inferioridade do nosso povo. Em suma, alimentávamos, em relação a nós próprios, praticamente todos os preconceitos e aprendemos a valorizar e admirar o alheio, o que é estrangeiro, e menosprezar o que é nosso, chegando a ter vergonha de nós mesmos.
Encerramento da Economia Açucareira:
A guerra realizada pela Holanda contra a Espanha modificou a nossa colonização, os grandes beneficiados foram os holandeses que passaram a ter praticamente todo o comércio dos países europeus realizado por mar, pois, era o meio de transporte mais rápido e importante da época. Sendo que, no Brasil, os batavos detiveram o controle da produção do açúcar, sendo um grande modificador para nossa economia.
Os holandeses, enquanto estiveram no Brasil, adquiriram todo o conhecimento de técnicas e organizações da indústria açucareira, pois, era isso o que eles precisavam para implantarem uma nova base industrial. A partir desse momento, estaria perdido o monopólio e alterado os dois grupos representativos da época, os portugueses produtores e os holandeses financiadores.
Assim, a partir de meados do século XVIII e durante todo o século XIX, o preço do açúcar permaneceu reduzido à metade. Sem recursos próprios para conter a desvalorização do açúcar o Governo de Portugal e os produtores portugueses mudam atenção para o café, no século XIX.
Dessa forma houve no próprio funcionamento do ciclo do açúcar, elementos negativos que impediram sua viabilidade ao progresso. Ocorrendo, então, o encerramento do monopólio da economia açucareira que manteve sua importância, porém deixou de ser o principal produto e a base de sustentação da economia brasileira.
A essa altura já se ia encerrando o ciclo do açúcar tendo como conseqüência o êxodo da população para a região de mineração no interior do Brasil.
Conclusão:
A cultura do açúcar surgiu, no Brasil, pela necessidade de colonizar a terra, para defendê-la e para explorar suas riquezas.
A importância dessa cultura pode ser exemplificada pelo interesse dos holandeses, que atravessaram mares para invadir Pernambuco, à época maior produtor de açúcar. Mesmo quando expulsos, os holandeses não abandoaram a produção de açúcar. Optaram pela transferência do know how do cultivo da cana e refino do produto para as Antilhas que, ao lado do Brasil, dominaram o comércio de açúcar na Europa nos séculos XVII e XVIII.
Embora essa cultura tenha sido responsável pela base de sustentação da economia e da colonização do nosso país durante os século XVI e XVII, o governo português não assegurou à sua colônia condições para manutenção do monopólio sobre seu domínio, que primeiro passa aos holandeses e posteriormente é compartilhado com os mesmos.
Também contribui para o declínio do produto a perda de importância do mesmo no mercado europeu em decorrência ao surgimento do açúcar de beterraba.
Assim, no século XIX, o açúcar deixa de ser principal produto nacional papel que passa, então, a ser exercido pelo café.
Autoria: Fabíola Schwartz
Assinar:
Postagens (Atom)