Logaritmo quociente

Logaritmo do quociente:




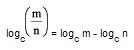
3. FUNÇÃO LOGARÍTMICA

É toda função f: que associa a cada x o logaritmo, na base b, de x:

f(x) = logb x

Exemplos:

a) f(x) = log3 x

b) g(x) = log1/3 x

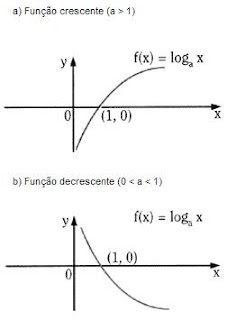
Gráficos da função logarítmica




Observações:

a) O gráfico da função logarítmica passa sempre pelo ponto (1,0).

b) O gráfico nunca toca o eixo y e não ocupa pontos dos quadrantes II e III.

c) Quando a > 1, a função logarítmica é crescente (x1 > x2 loga x1 > loga x2).

d) Quando 0 < a <1 data-blogger-escaped-a="" data-blogger-escaped-decrescente="" data-blogger-escaped-fun="" data-blogger-escaped-logar="" data-blogger-escaped-o="" data-blogger-escaped-tmica="" data-blogger-escaped-x1=""> x2 loga x1 < loga x2).


4. EQUAÇÕES LOGARÍTMICAS

Para resolver equações logarítmicas, devemos aplicar as propriedades e, em seguida, verificar se os valores obtidos para a incógnita estão de acordo com as condições de existência estabelecidas.

Exemplo:

Resolver a equação log2 x + log2 2x = 3.

Solução:

Condições de existência:



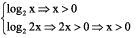
Aplicando a propriedade do logaritmo do produto, e a definição de logaritmo, temos:

log2 x + log2 2x = 3 →log2 (x . 2x) = 3 →

log2 2x2 = 3 →23 = 2x2 →8 = 2x2 → x2 = 4→ x = 2 ou x = -2

Comparando os valores obtidos com as condições de existência estabelecidas, verificamos que – 2 é um valor impróprio.

Logo:

V = {2}