Considere o triângulo de vértices A, B e C abaixo. Os pontos M, N e P são os pontos médios dos lados AB, BC e AC, respectivamente. Os segmentos de reta MC, AN e PB são as medianas do triângulo. Denominamos baricentro (G) de um triângulo o ponto de encontro das medianas.
Agora vamos considerar um triângulo no plano cartesiano de vértices A(xA, yA), B(xB, yB) e C(xC, yC) e baricentro G(xG, yG).
As coordenadas do baricentro do triângulo ABC serão dadas por:

Exemplo 1. Determine as coordenadas do baricentro do triângulo de vértices A(2, 7), B(5, 3) e C(2, 2).
Solução: Vamos calcular as coordenadas do Baricentro do triângulo separadamente, para não haver confusão no entendimento da fórmula, que é muito simples.
Sabemos que:
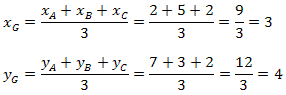
Portanto, o baricentro do triângulo ABC tem coordenadas G(3, 4).
Exemplo 2. Determine as coordenadas do vértice B do triângulo ABC sabendo que seu baricentro tem coordenadas G(5, 8) e que os outros dois vértices são A(5, 8) e C(7, 6).
Solução: Como conhecemos as coordenadas do baricentro do triângulo e as coordenadas de dois vértices, vamos utilizar a fórmula para a determinação do baricentro para determinar as coordenadas de B.
Segue que:
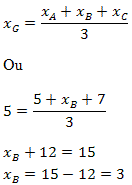
Temos também que:

Portanto, o vértice B tem coordenadas B(3, 10).
Marcelo Rigonatto

Exemplo 1. Determine as coordenadas do baricentro do triângulo de vértices A(2, 7), B(5, 3) e C(2, 2).
Solução: Vamos calcular as coordenadas do Baricentro do triângulo separadamente, para não haver confusão no entendimento da fórmula, que é muito simples.
Sabemos que:
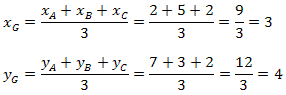
Portanto, o baricentro do triângulo ABC tem coordenadas G(3, 4).
Exemplo 2. Determine as coordenadas do vértice B do triângulo ABC sabendo que seu baricentro tem coordenadas G(5, 8) e que os outros dois vértices são A(5, 8) e C(7, 6).
Solução: Como conhecemos as coordenadas do baricentro do triângulo e as coordenadas de dois vértices, vamos utilizar a fórmula para a determinação do baricentro para determinar as coordenadas de B.
Segue que:
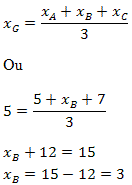
Temos também que:

Portanto, o vértice B tem coordenadas B(3, 10).
Nenhum comentário:
Postar um comentário