Ângulos formados por duas retas

Considere duas retas distintas e concorrentes do plano, r e s, ambas oblíquas aos eixos coordenados e não perpendiculares entre si. As duas retas formam um ângulo entre si, que denominaremos de α. Esse ângulo α é tal que:

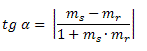
Onde m_s e m_r são os coeficientes angulares das retas s e r, respectivamente.
Se ocorrer de uma das retas ser vertical e a outra oblíqua, o ângulo α formado entre elas é tal que:

Exemplo 1. Determine o ângulo formado entre as retas r: x - y = 0 e s: 3x + 4y – 12 =0

Solução: Para determinar o ângulo formado entre as duas retas, precisamos conhecer o coeficiente angular de cada uma delas. Assim, vamos determinar o coeficiente angular das retas r e s.

Para a reta r, temos:

x - y = 0
y = x

Portanto, m_r = 1.
Para a reta s, temos:

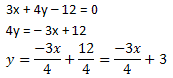
Portanto, m_s = -3/4
Conhecendo os valores dos coeficientes angulares, basta aplicar a fórmula do ângulo entre duas retas:

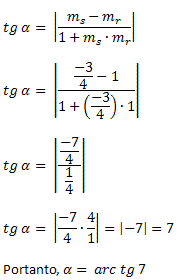
Exemplo 2. Determine o ângulo formado entre as retas r: y = 3x + 4 e s: y = – 2x + 8.

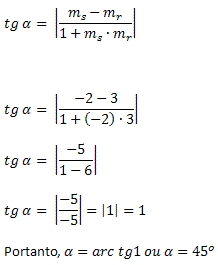
Solução: Vamos determinar o coeficiente angular de cada uma das retas dadas.

Para a reta r, temos:
y = 3x + 4
m_r = 3
Para a reta s, temos:
y = – 2x + 8
m_s = – 2
Aplicando a fórmula do ângulo entre duas retas, obtemos:

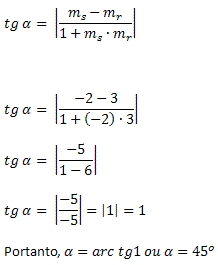
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática