Área do Segmento Circular

Um conjunto de pontos que possuem a mesma distância de um ponto central é denominado círculo ou circunferência. O círculo é a área interna e circunferência é o limite do círculo. Observe:

Toda região circular possui comprimento e área, que dependem do tamanho do raio, que é a distância do centro até a extremidade do corpo circular.

Todo segmento de reta que liga dois pontos de uma circunferência recebe o nome de corda. A corda que passa pelo centro, dividindo a região em duas partes iguais, é chamada de diâmetro e corresponde ao dobro da medida do raio.

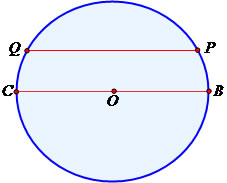
QP: corda da região circular

CB: é uma corda que passa pelo centro, dessa forma recebe o nome de diâmetro.

O segmento de uma região circular é limitado por uma corda e um arco. Observe:

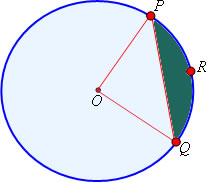
Para determinarmos a área do segmento circular PQR formado pela corda PQ, devemos realizar o seguinte cálculo:

Área do segmento circular = Área do setor OPRQ – Área do triângulo OPQ


Nos casos em que o segmento é maior que o semicírculo, utilizamos a seguinte condição:

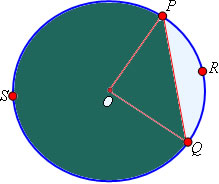
Área do segmento circular = Área do setor OPSQ + Área do triângulo POQ
mundoeducacao