Poliedros

Poliedros são sólidos geométricos ou figuras geométricas espaciais formadas por três elementos básicos: faces, arestas e vértices.

Os Poliedros podem ser convexos e não convexos.

Ao estudarmos os poliedros convexos verificamos uma importante relação existente entre o número de faces, arestas e vértices. Leonhard Euler foi um matemático suíço que, dentre várias contribuições para a Matemática, desenvolveu uma relação que calcula o número de arestas (A), faces (F) e vértices (V) de um poliedro, desde que haja dois valores.

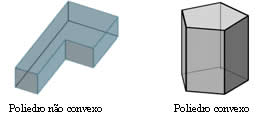
Relação de Euler: V – A + F = 2 ou V + F = A + 2
Exemplo 1
Calcule o número de arestas de um sólido que possui 8 vértices e 6 faces.

V – A + F = 2
8 – A + 6 = 2
A = 14 – 2
A = 12

Exemplo 2
Um sólido geométrico tem 6 vértices e 10 arestas. Calcule o número de faces desse sólido.

V – A + F = 2
6 – 10 + F = 2
F = 2 + 4
F = 6

Poliedros de PlatãoTodo poliedro considerado de Platão deve obedecer algumas condições:

O número de arestas tem que ser igual ao número de faces.
Os ângulos do poliedro devem possuir o mesmo número de arestas.
A equação de Euler precisa ser aplicada e aceita.

Poliedros regulares
Todas as faces iguais e regulares
Os ângulos poliédricos precisam possuir o mesmo valor.

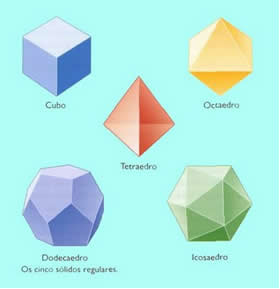
Temos a certeza da existência de cinco poliedros regulares, os chamados poliedros de Platão: tetraedro, hexaedro ou cubo, dodecaedro, octaedro e icosaedro.

www.mundoeducacao.com.br