Uma matriz constitui uma ferramenta matemática utilizada em diversas situações relacionadas à Informática e Engenharia. Elas são formadas por elementos distribuídos em linhas e colunas (aij), onde i: linhas e j: colunas. As matrizes possuem inúmeras situações especiais, como matriz coluna, matriz quadrada, matriz nula, matriz identidade, matriz diagonal e matriz triangular.
Vamos abordar as características de uma matriz triangular, classificada em superior ou inferior. Observe:
Matriz triangular superior
Matriz em que os elementos abaixo da diagonal principal são iguais a zero.
Vamos abordar as características de uma matriz triangular, classificada em superior ou inferior. Observe:
Matriz triangular superior
Matriz em que os elementos abaixo da diagonal principal são iguais a zero.

Matriz triangular inferior
Matriz em que os elementos acima da diagonal são iguais a zero.
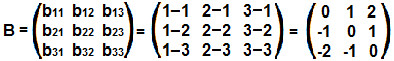
Dada a matriz triangular
 , calcularemos o seu determinante aplicando Sarrus e, logo na sequência, verificar se o valor do determinante corresponde à multiplicação dos elementos da diagonal principal da matriz triangular.
, calcularemos o seu determinante aplicando Sarrus e, logo na sequência, verificar se o valor do determinante corresponde à multiplicação dos elementos da diagonal principal da matriz triangular.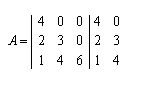
Aplicando Sarrus
Diagonal principal
4 * 3 * 6 = 72
0 * 0 * 1 = 0
0 * 2 * 4 = 0
72 + 0 + 0 = 72
Diagonal secundária
0 * 2 * 6 = 0
4 * 0 * 4 = 0
0 * 3 * 1 = 0
–16 + 0 + 0 = –16
Determinante de A72 + 0
72
Multiplicando os elementos da diagonal principal
4 * 3 * 6 = 72
Observe que os resultados são os mesmos, portanto, a regra para o cálculo do determinante nas matrizes triangulares é válida.
Nenhum comentário:
Postar um comentário