Equações paramétricas da reta

Marcelo Rigonatto

Equações da reta

A geometria analítica estuda as formas geométricas do ponto de vista da álgebra, utilizando equações para analisar o comportamento e os elementos dessas figuras. A reta é uma das formas geométricas estudas pela geometria analítica, possuindo três tipos de equações: equação geral, equação reduzida e equação paramétrica.

As equações paramétricas são duas equações que representam a mesma reta utilizando uma incógnita t. Essa incógnita recebe o nome de parâmetro e faz a ligação entre as duas equações que representam a mesma reta.

As equações x = 5 + 2t e y = 7 + t são as equações paramétricas de uma reta s. Para obter a equação geral dessa reta, basta isolar t em uma das equações e substituir na outra. Vejamos como isso é realizado.

As equações paramétricas são:
x = 5 + 2t (I)
y = 7 + t (II)

Isolando t na equação (II), obtemos t = y – 7. Vamos substituir o valor de t na equação (I).
x = 5 + 2(y – 7)
x = 5 + 2y – 14
x – 2y + 9 = 0 → equação geral da reta s.

Exemplo 1. Determine a equação geral da reta de equações paramétricas abaixo.
x = 8 – 3t
y = 1 – t

Solução: Devemos isolar t em uma das equações e substituir na outra. Assim, segue que:

x = 8 – 3t (I)
y = 1 – t (II)

Isolando t na equação (II), obtemos:
y – 1 = – t
ou
t = – y + 1

Substituindo na equação (II), teremos:
x = 8 – 3(– y + 1)
x = 8 + 3y – 3
x = 5 + 3y
x – 3y – 5 = 0 → equação geral da reta

Nos dois exemplos feitos obtemos a equação geral da reta através das equações paramétricas. O contrário também pode ser feito, ou seja, utilizar a equação geral da reta para obter a equação paramétrica.

Exemplo 2. Determine as equações paramétricas da reta r de equação geral 2x – y -15 = 0.
Solução: Para determinar as equações paramétricas da reta r a partir da equação geral, devemos proceder da seguinte forma:

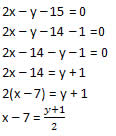
Podemos fazer:

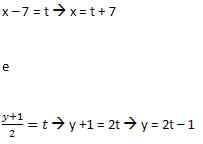
Assim, as equações paramétricas da reta são:
x = t + 7 e y = 2t – 1