Função exponencial

A principal característica de uma função exponencial é o aparecimento da variável no expoente. Esse tipo de função expressa situações onde ocorre grandes variações em períodos curtos. As exponenciais, como são conhecidas, possuem diversas aplicações no cotidiano, na Matemática financeira está presente nos cálculos relacionados aos juros compostos, pois ocorre acumulação de capital durante o período da aplicação. Vamos analisar alguns exemplos e verificar a praticidade das funções exponenciais.

Exemplos

Num depósito a prazo efetuado em um banco, o capital acumulado ao fim de certo tempo é dado pela fórmula C = D * (1 + i)^t, onde C representa o capital acumulado, D o valor do depósito, i a taxa de juros ao mês e t o tempo de meses em que o dinheiro está aplicado. Nesse sistema, ao final de cada mês os juros capitalizados são incorporados ao depósito.

a) Para um depósito de R$ 1 000,00, com taxa de 2% ao mês, qual o capital acumulado ao fim de 6 meses? E de 1 ano?

6 meses
C = D * (1 + i)^t
C = 1000 * (1 + 0,02)⁶
C = 1000 * 1,02⁶
C = 1000 * 1,126162419264
C = 1 126,16
O capital acumulado será de R$ 1.126,16.

1 ano = 12 meses

C = D * (1 + i)^t
C = 1000 * 1,02¹²
C = 1000 * 1,268241794562545318301696
C = 1 268,24
O capital acumulado será de R$ 1.268,24.


b) Para um depósito de R$ 5 000,00, a uma taxa de 5% ao mês, qual o capital acumulado durante 4 meses?

C = D * (1 + i)^t
C = 5000 * (1 + 0,05)⁴
C = 5000 * 1,05⁴
C = 5000 * 1,21550625
C = 6 077,53
O capital acumulado será de R$ 6.077,53.


c) Para um depósito de R$ 2 500,00, a uma taxa de juros de 10% ao ano, qual será o capital acumulado durante 10 anos?

C = D * (1 + i)^t
C = 2500 * (1 + 0,1)¹⁰
C = 2500 * 1,01¹⁰
C = 2500 * 2,5937424601
C = 6484,36
O capital acumulado em 10 anos será de R$ 6.484,36.
Dizemos que uma função é exponencial quando a variável se encontra no expoente de um número real, sendo que esse número precisa ser maior que zero e diferente de um. Podemos explicitar tal condição usando a seguinte definição geral:

f: R→R tal que y = ax, sendo que a > 0 e a ≠ 1.


O gráfico de uma função exponencial é definido de acordo com o valor da base a, observe os dois gráficos a seguir:

a > 0 0 < a < 1

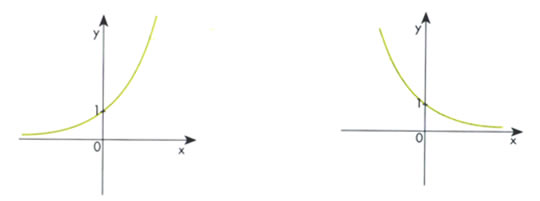
A função exponencial é caracterizada pelo crescimento e decrescimento muito rápido, por isso é muito utilizada na Matemática e em outras ciências correlacionadas com cálculos, como: Química, Biologia, Física, Engenharia, Astronomia, Economia, Geografia, entre outras. Na Matemática, serve para demonstrar o crescimento de um capital aplicado a uma determinada taxa de juros compostos. Na Química está diretamente ligada ao decaimento radioativo, na Biologia se apresenta em situações envolvendo o crescimento de bactérias em uma colônia. Usada também na Geografia no intuito de determinar o crescimento populacional.

O gráfico de uma função exponencial permite o estudo de situações que se enquadram em uma curva de crescimento ou decrescimento, sendo possível analisar as quantidades relacionadas à curva, por isso os Psicólogos e Educadores utilizam-se da exponencial a fim de demonstrarem as curvas de aprendizagem.
Em razão dessa propriedade, a função exponencial é considerada uma importante ferramenta da Matemática, abrangendo diversas situações cotidianas e contribuindo de forma satisfatória na obtenção de resultados que exigem uma análise quantitativa e qualitativa.

mundoeducacao