 O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas. Existem outras formas cilíndricas diferentes das comuns, como por exemplo o cilindro sinuzoidal obtido pela translação da função seno.
O conceito de cilindro é muito importante. Nas cozinhas encontramos aplicações intensas do uso de cilindros. Nas construções, observamos caixas d'água, ferramentas, objetos, vasos de plantas, todos eles com formas cilíndricas. Existem outras formas cilíndricas diferentes das comuns, como por exemplo o cilindro sinuzoidal obtido pela translação da função seno. Aplicações práticas: Os cilindros abaixo recomendam alguma aplicação importante em sua vida?



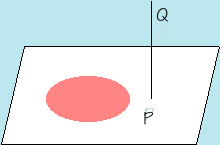 Seja P um plano e nele vamos construir um círculo de raio r. Tomemos também um segmento de reta PQ que não seja paralelo ao plano P e nem esteja contido neste plano P.
Seja P um plano e nele vamos construir um círculo de raio r. Tomemos também um segmento de reta PQ que não seja paralelo ao plano P e nem esteja contido neste plano P. Um cilindro circular é a reunião de todos os segmentos congruentes e paralelos a PQ com uma extremidade no círculo.
Observamos que um cilindro é uma superfície no espaço R3, mas muitas vezes vale a pena considerar o cilindro com a região sólida contida dentro do cilindro. Quando nos referirmos ao cilindro como um sólido usaremos aspas, isto é, "cilindro" e quando for à superfície, simplesmente escreveremos cilindro.
A reta que contém o segmento PQ é denominada geratriz e a curva que fica no plano do "chão" é a diretriz.
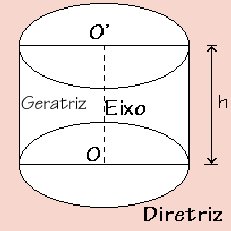
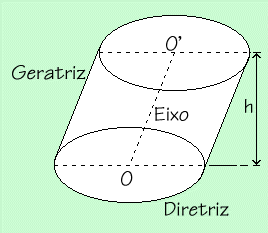
Objetos geométricos em um "cilindro"
Num cilindro, podemos identificar vários elementos:
- Base
É a região plana contendo a curva diretriz e todo o seu interior. Num cilindro existem duas bases. - Eixo
É o segmento de reta que liga os centros das bases do "cilindro". - Altura
A altura de um cilindro é a distância entre os dois planos paralelos que contêm as bases do "cilindro". - Superfície Lateral
É o conjunto de todos os pontos do espaço, que não estejam nas bases, obtidos pelo deslocamento paralelo da geratriz sempre apoiada sobre a curva diretriz. - Superfície Total
É o conjunto de todos os pontos da superfície lateral reunido com os pontos das bases do cilindro. - Área lateral
É a medida da superfície lateral do cilindro. - Área total
É a medida da superfície total do cilindro. - Seção meridiana de um cilindro
É uma região poligonal obtida pela interseção de um plano vertical que passa pelo centro do cilindro com o cilindro.
As características apresentadas anteriormente para cilindros circulares, são também possíveis para outros tipos de curvas diretrizes, como: elipse, parábola, hipérbole, seno ou outra curva simples e suave num plano.
Mesmo que a diretriz não seja uma curva conhecida, ainda assim existem cilindros obtidos quando a curva diretriz é formada por uma reunião de curvas simples. Por exemplo, se a diretriz é uma curva retangular, temos uma situação patológica e o cilindro recebe o nome especial de prisma.
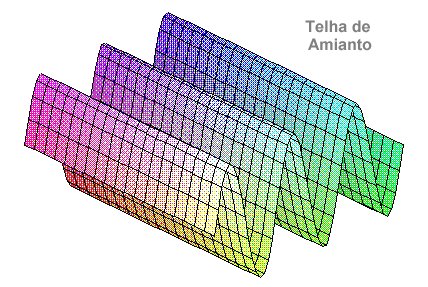
Em função da curva diretriz, o cilindro terá o nome de cilindro: elíptico, parabólico, hiperbólico, sinuzoidal (telha de eternit).
- Cilindro circular oblíquo
Apresenta as geratrizes oblíquas em relação aos planos das bases. - Cilindro circular reto
As geratrizes são perpendiculares aos planos das bases. Este tipo de cilindro é também chamado de cilindro de revolução, pois é gerado pela rotação de um retângulo. - Cilindro eqüilátero
É um cilindro de revolução cuja seção meridiana é um quadrado.
Em um cilindro, o volume é dado pelo produto da área da base pela altura.
V = Abase × h
Se a base é um círculo de raio r, então:
V = 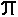 r2 h
r2 h
Exercício: Calcular o volume de um cilindro oblíquo com base elíptica (semi-eixos a e b) e altura h. Sugestão: Veja nesta mesma Página um material sobre a área da região elíptica.Áreas lateral e total de um cilindro circular reto
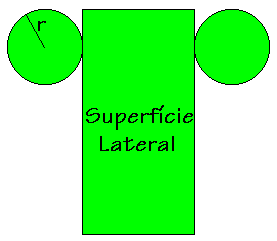 Quando temos um cilindro circular reto, a área lateral é dada por:
Quando temos um cilindro circular reto, a área lateral é dada por: Alat = 2
onde r é o raio da base e h é a altura do cilindro.
Atot = Alat + 2 Abase
Atot = 2
Atot = 2

Exercício: Dado o cilindro circular equilátero (h=2r), calcular a área lateral e a área total.
No cilindro equilátero, a área lateral e a área total é dada por:
Alat = 2
Atot = Alat + 2 Abase
Atot = 4
V = Abase h =
Exercício: Seja um cilindro circular reto de raio igual a 2cm e altura 3cm. Calcular a área lateral, área total e o seu volume.
- Cálculo da Área lateral
Alat = 2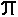 r h = 2
r h = 2 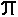 2.3 = 12
2.3 = 12 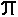 cm2
cm2 - Cálculo da Área total
Atot = Alat + 2 Abase
Atot = 12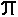 + 2
+ 2 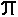 22 = 12
22 = 12 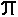 + 8
+ 8 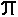 = 20
= 20 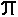 cm2
cm2 - Cálculo do Volume
V = Abase × h =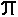 r2 × h
r2 × h
V =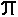 22 × 3 =
22 × 3 = 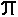 × 4 × 3 = 12
× 4 × 3 = 12 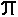 cm33
cm33
Nenhum comentário:
Postar um comentário