Todo polígono regular pode ser inscrito em uma circunferência. Ao decompormos esse polígono notamos várias regiões triangulares, então se o polígono for decomposto em n triângulos basta calcularmos sua área e multiplicarmos pelo número de triângulos.
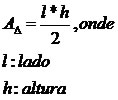
Obs.: O número de lados da figura é igual ao número de triângulos que compõem a figura.
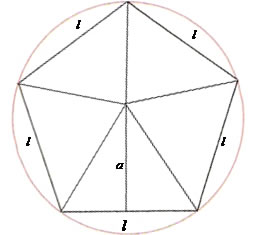
No pentágono inscrito abaixo podemos notar que a altura de cada triângulo que o compõe corresponde ao apótema do polígono, podemos substituir a altura h pelo apótema a, na expressão que calcula a área de cada triângulo:
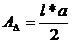
Para calcular a área total basta multiplicarmos a expressão da área de cada triângulo pelo perímetro do polígono e dividir por dois como demonstra a expressão final:
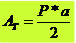
Vamos calcular a área de um pentágono regular, onde cada lado mede 4m.
Já vimos que o pentágono é formado por cinco triângulos e vale lembrarmos que em qualquer polígono a soma dos ângulos externos é sempre igual a 360º. Para calcularmos o apótema deste triângulo devemos recorrer à relação trigonométrica tangente. Veja que o apótema divide a base em duas partes iguais.
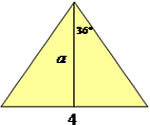
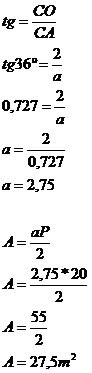
A área total de um pentágono cujo lado mede 4 metros é de 27,5 m2.
Marcos Noé
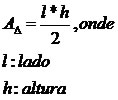
Obs.: O número de lados da figura é igual ao número de triângulos que compõem a figura.
No pentágono inscrito abaixo podemos notar que a altura de cada triângulo que o compõe corresponde ao apótema do polígono, podemos substituir a altura h pelo apótema a, na expressão que calcula a área de cada triângulo:
Para calcular a área total basta multiplicarmos a expressão da área de cada triângulo pelo perímetro do polígono e dividir por dois como demonstra a expressão final:

Vamos calcular a área de um pentágono regular, onde cada lado mede 4m.
Já vimos que o pentágono é formado por cinco triângulos e vale lembrarmos que em qualquer polígono a soma dos ângulos externos é sempre igual a 360º. Para calcularmos o apótema deste triângulo devemos recorrer à relação trigonométrica tangente. Veja que o apótema divide a base em duas partes iguais.

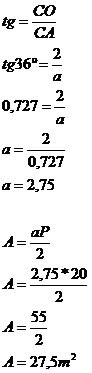
A área total de um pentágono cujo lado mede 4 metros é de 27,5 m2.
Marcos Noé
Comentários
Postar um comentário