Dizimas

Dízimas periódicas

Há frações que não possuem representações decimal exata. Por exemplo:

Aos numerais decimais em que há repetição periódica e infinita de um ou mais algarismos, dá-se o nome de numerais decimais periódicos ou dízimas periódicas.

Numa dízima periódica, o algarismo ou algarismos que se repetem infinitamente, constituem o período dessa dízima.

As dízimas classificam-se em dízimas periódicas simples e dízimas periódicas compostas. Exemplos:

(período: 5)

(período: 3)

(período: 12)

São dízimas periódicas simples, uma vez que o período apresenta-se logo após a vírgula.

Período: 2 Parte não periódica: 0

Período: 4 Período não periódica: 15

Período: 23 Parte não periódica: 1

São dízimas periódicas compostas, uma vez que entre o período e a vírgula existe uma parte não periódica.

Observações:

Consideramos parte não periódica de uma dízima o termo situado entre vírgulas e o período. Excluímos portanto da parte não periódica o inteiro.

Podemos representar uma dízima periódica das seguintes maneiras:

Geratriz de uma dízima periódica

É possível determinar a fração (número racional) que deu origem a uma dízima periódica. Denominamos esta fração de geratriz da dízima periódica.

Procedimentos para determinação da geratriz de uma dízima:

Dízima simples

A geratriz de uma dízima simples é uma fração que tem para numerador o período e para denominador tantos noves quantos forem os algarismos do período.

Exemplos:

Dízima Composta:
A geratriz de uma dízima composta é uma fração da forma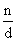 , onde

n é a parte não periódica seguida do período, menos a parte não periódica. d tantos noves quantos forem os algarismos do período seguidos de tantos zeros quantos forem os algarismos da parte não periódica.

Exemplos: