Um sistema linear pode ser resolvido através do método da substituição ou cabelo método de Cramer, com o auxílio da régua de Sarrus. Uma nova forma de resolução será apresentada no intuito de ampliar as técnicas capaz de determinar os valores das incógnitas de UM sistema de equações lineares. Vamos demonstrar como o escalonamento de UM sistema na forma de matriz completa dos coeficientes. Observe:
Dado o sistema de equações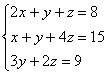 , vamos escreve-lo na forma de umha matriz completa dos coeficientes.
, vamos escreve-lo na forma de umha matriz completa dos coeficientes.
Dado o sistema de equações
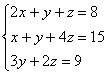 , vamos escreve-lo na forma de umha matriz completa dos coeficientes.
, vamos escreve-lo na forma de umha matriz completa dos coeficientes.
Vamos subtrair os itens LINHA 2 (L2) Pela metade dos elementos da LINHA 1 (L1).
L2 - L1 * 1/2

Vamos subtrair os itens LINHA 3 (L3) Cabelo sêxtupla dos elementos da LINHA 2 (L2).
L3 - 6 * L2
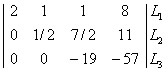
L2 - L1 * 1/2

Vamos subtrair os itens LINHA 3 (L3) Cabelo sêxtupla dos elementos da LINHA 2 (L2).
L3 - 6 * L2
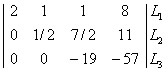
Observe que ao realizarmos as Operaçõe demonstradas, conseguimos zerar alguns elementos da matriz e, respectivamente, coeficientes do sistema de equações. Veja o sistema simplificado que obtemos com o escalonamento da matriz completa dos coeficientes numéricos:
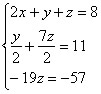
-19z = -57
19z = 57
z = 57/19
z = 3
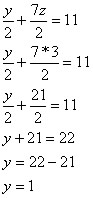
2x + y + z = 8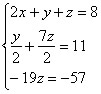
-19z = -57
19z = 57
z = 57/19
z = 3
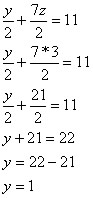
2x + 1 + 3 = 8
2x = 8 - 4
2x = 4
x = 2
O conjunto solução do sistema proposto é: x = 2, y = 1 ez = 3.
O sistema de escalonamento de matrizes completas dos coeficientes numéricos de UM sistema de equações lineares possuia a finalidade de simplificar o sistema através de Operaçõe entre os elementos pertencentes às Linhas da matriz.
www.mundoeducacao.com.br
Calculadora: escalonar matriz.
ResponderExcluirhttps://mathematicalramblings.blogspot.com/2019/08/calculadora-escalonar-matriz.html