Relações métricas no triângulo retângulo

Marcelo Rigonatto

Triângulo retângulo

O triângulo é o polígono com menor número de lados, mas é uma das formas geométricas mais importantes no estudo da geometria. Sempre intrigou matemáticos desde a Antiguidade. Triângulo retângulo é aquele que apresenta um ângulo interno medindo 90^o. Esse tipo de triângulo apresenta propriedades e características muito relevantes. Faremos o estudo das relações entre as medidas dos lados do triângulo retângulo.

Todo triângulo retângulo é composto por dois catetos e uma hipotenusa. A hipotenusa é o maior lado do triângulo retângulo e está oposto ao ângulo reto.

Observe a figura abaixo.

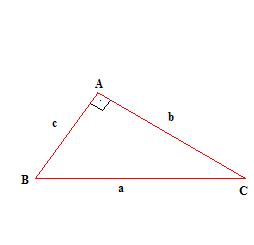
Temos que:
a → é a hipotenusa
b e c → são os catetos.

A perpendicular a BC, traçada por A, é a altura h, relativa à hipotenusa do triângulo.

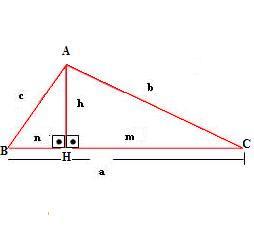
BH = n e CH = m são as projeções dos catetos sobre a hipotenusa.

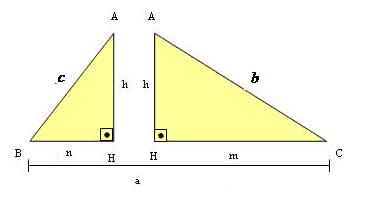
Os três triângulos são semelhantes

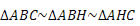
Da semelhança de triângulos obtemos as seguintes relações:

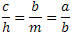
Daí segue que:

b² = am e ah = bc

Temos, também, as seguintes relações:

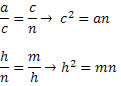
E a mais famosa das relações métricas no triângulo retângulo:

a² = b² + c²

Que é o teorema de Pitágoras.

Observe que temos cinco relações métricas no triângulo retângulo:

1. b² = am
2. ah = bc
3. c² = an
4. h² = mn
5. a² = b² + c²

Todas elas são de grande utilidade na resolução de problemas que envolvem triângulos retângulos.

Exemplo. Determine as medidas da altura relativa à hipotenusa e dos dois catetos do triângulo abaixo.

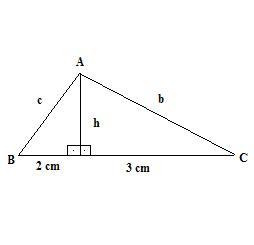
Solução: Temos que

n = 2 cm
m = 3 cm

Utilizando a quarta relação descrita anteriormente, obtemos:

h² = mn
h² = 3∙2
h² = 6
h = √6
Segue que:

a = 2 + 3 = 5 cm

Daí, utilizando a primeira relação, obtemos:

b² = am
b² = 5∙3
b² = 15
b = √15

Da terceira relação, obtemos:

c² = an
c² = 5∙2
c² = 10
c = √10