Regra de três Composta

Regra de três composta

A regra de três composta é utilizada em problemas com mais de duas grandezas, direta ou inversamente proporcionais.
Exemplos:
1) Em 8 horas, 20 caminhões descarregam 160m³ de areia. Em 5 horas, quantos caminhões serão necessários para descarregar 125m³?
Solução: montando a tabela, colocando em cada coluna as grandezas de mesma espécie e, em cada linha, as grandezas de espécies diferentes que se correspondem:

Horas	Caminhões	Volume
8	20	160
5	x	125

Identificação dos tipos de relação: Inicialmente colocamos uma seta para baixo na coluna que contém o x (2ª coluna).

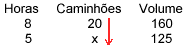
A seguir, devemos comparar cada grandeza com aquela onde está o x.
Observe que:
Aumentando o número de horas de trabalho, podemos diminuir o número de caminhões. Portanto a relação é inversamente proporcional (seta para cima na 1ª coluna).

Aumentando o volume de areia, devemos aumentar o número de caminhões. Portanto a relação é diretamente proporcional (seta para baixo na 3ª coluna). Devemos igualar a razão que contém o termo x com o produto das outras razões de acordo com o sentido das setas.

Montando a proporção e resolvendo a equação temos:

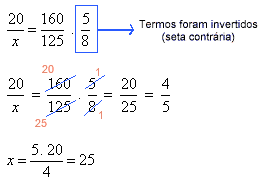Logo, serão necessários 25 caminhões.

---

2) Numa fábrica de brinquedos, 8 homens montam 20 carrinhos em 5 dias. Quantos carrinhos serão montados por 4 homens em 16 dias?
Solução: montando a tabela:

Homens	Carrinhos	Dias
8	20	5
4	x	16

Observe que:
Aumentando o número de homens, a produção de carrinhos aumenta. Portanto a relação é diretamente proporcional (não precisamos inverter a razão).

Aumentando o número de dias, a produção de carrinhos aumenta. Portanto a relação também é diretamente proporcional (não precisamos inverter a razão). Devemos igualar a razão que contém o termo x com o produto das outras razões.

Montando a proporção e resolvendo a equação temos:

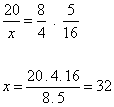
Logo, serão montados 32 carrinhos.

---

3) Dois pedreiros levam 9 dias para construir um muro com 2m de altura. Trabalhando 3 pedreiros e aumentando a altura para 4m, qual será o tempo necessário para completar esse muro?
Inicialmente colocamos uma seta para baixo na coluna que contém o x. Depois colocam-se flechas concordantes para as grandezas diretamente proporcionais com a incógnita e discordantes para as inversamente proporcionais, como mostra a figura abaixo:

Montando a proporção e resolvendo a equação temos:

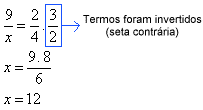
Logo, para completar o muro serão necessários 12 dias.

---

Exercícios complementares
Agora chegou a sua vez de tentar. Pratique tentando fazer esses exercícios:
1) Três torneiras enchem uma piscina em 10 horas. Quantas horas levarão 10 torneiras para encher 2 piscinas? Resposta: 6 horas.
2) Uma equipe composta de 15 homens extrai, em 30 dias, 3,6 toneladas de carvão. Se for aumentada para 20 homens, em quantos dias conseguirão extrair 5,6 toneladas de carvão? Resposta: 35 dias.
3) Vinte operários, trabalhando 8 horas por dia, gastam 18 dias para construir um muro de 300m. Quanto tempo levará uma turma de 16 operários, trabalhando 9 horas por dia, para construir um muro de 225m? Resposta: 15 dias.
4) Um caminhoneiro entrega uma carga em um mês, viajando 8 horas por dia, a uma velocidade média de 50 km/h. Quantas horas por dia ele deveria viajar para entregar essa carga em 20 dias, a uma velocidade média de 60 km/h? Resposta: 10 horas por dia.
5) Com uma certa quantidade de fio, uma fábrica produz 5400m de tecido com 90cm de largura em 50 minutos. Quantos metros de tecido, com 1 metro e 20 centímetros de largura, seriam produzidos em 25 minutos? Resposta: 2025
www.somatematica.com.br