Som

SomO ouvido íntegro pode ser sensibilizado por uma onda mecânica que se propaga num campo ondulatório (meio material), como o ar, desde que essa onda apresente intensidade suficiente e sua freqüência encontre-se dentro de um certo intervalo subjetivo. À estas sensibilizações denominaremos por sensações sonoras. Em geral, ao estudo da produção (fontes sonoras), propagação e fenômenos correlatos sofridos pela onda mecânica sonora ou audível, denomina-se Acústica e, em particular, denominaremos por som à toda onda mecânica nas condições acima especificadas (intensidade suficiente e freqüência limitada num certo intervalo). Se a freqüência da onda sonora pertence ao intervalo subjetivo (depende do observador), 16Hz -------- 20000 Hz, esse som é audível para o ser humano.
Ultra-som e Infra-somOndas longitudinais de freqüências superiores a 20 kHz, caracterizam sons inaudíveis e denominam-se ultra-sons; e aquelas de freqüências inferiores a 16 Hz, também inaudíveis, são ditas infra-sons.

Escala das Ondas Mecânicas

Freqüência Hz	Denominação	Método de excitação	Aplicação
0,5 ---- 20	Infra-sons	Vibração da água em grandes reservatórios, batidas do coração.	Prognóstico do tempo, diagnóstico de doenças do coração.
20 ---- 2.104	Sons Audíveis	Voz humana e dos a- nimais, instrumentos musicais, apitos, se- reias, alto-falantes ...	Para comunicação e si- nalização, assim como para a medição de dis- tâncias.
2.104---- 1010	Ultra-sons	Emissores magnetos- trictivos e piezoelétri- cos, apitos de Galton, também são excitados por alguns animais e insetos (morcegos, gri- los, gafanhotos etc.)	Deteção submarina por eco, limpeza e deteção de defeitos em peças e estruturas de constru- ções, aceleração de re- ações químicas, inves- tigação em medicina, biologia e física molecu- lar.
1011 ....	Hipersons	Vibrações térmicas das moléculas	Em investigações cien- tíficas.

Como citamos na tabela acima, os ultra-sons de altas potencias podem ser produzidos por emissores piezelétricos (quartzo vibrante) e encontram larga aplicação nos sonares. Em Química, os ultra-sons provocam oxidações e despolimerizações; em Físico-Química, fazem cessar estados de equilíbrio instáveis (superfusão, supersaturação) e impressionam a chapa fotográfica. Em Física, provocam a coagulação dos aerossóis, determinam nos líquidos o fenômeno de cavitação, excitam a luminescência de certos líquidos. Em Biologia, determinam a segmentação dos microrganismos e, por vezes, sua destruição (aplicação a esterilização do leite).
Sons Musicais e Ruídos
Quanto ao efeito sobre o ouvido, os sons são classificados em sons musicais e ruídos. Subjetivamente esta classificação deixa muito a desejar, pois há quem (muito propriamente) considere o rock'n rol um ruído e outros (mais desprovidos de sensibilidade) um som musical.

Fisicamente, entende-se por som musical ao resultado da superposição de ondas sonoras periódicas ou aproximadamente periódicas; ruídos correspondem a ondas sonoras não-periódicas e breves, que mudam imprevisivelmente de características. O som musical pode ser simples, quando corresponde a uma única onda harmônica e composto quando compõe-se de duas ou mais ondas harmônicas.

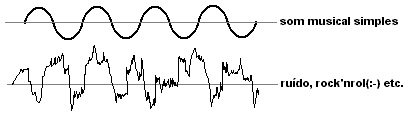
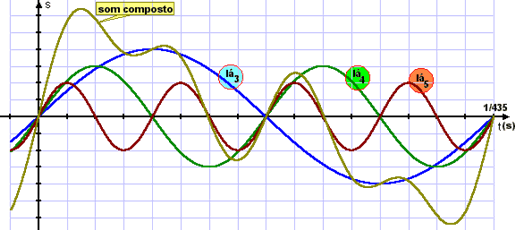Superposição de 3 sons musicais simples (lá3,lá4 e lá5) resultando num som composto.

Fontes SonorasÉ todo e qualquer dispositivo capaz de produzir ondas sonoras num meio material elástico (campo ondulatório); citaremos alguns de destaque em Acústica:

a) cordas vibrantes — violão — violino — piano — cordas vocais etc.
b) tubos sonoros — órgão - flauta — clarineta — oboé etc.
c) membranas e placas vibrantes: tambor — címbalos etc.
d) hastes vibrantes: diapasão — “triangulo” etc.

Qualidades Fisiológicas do SomOs sons simples distinguem-se uns dos outros por duas características, a saber, INTENSIDADE e ALTURA; os sons compostos, além daquelas, diferenciam-se pelo TIMBRE.
A intensidade fisiológica do som esta ligada à amplitude das vibrações (e, portanto à energia transportada pela onda sonora); é a qualidade pela qual um som forte (grande amplitude — muita energia) se distingue de um som fraco (pequena amplitude — pouca energia).

Apesar de variarem num mesmo sentido, é preciso não confundir intensidade fisiológica (ou intensidade auditiva ou ainda nível sonoro) com a intensidade física (ou intensidade sonora, quando se trata de onda sonora) da onda que é uma grandeza física associada ao fenômeno vibratório. Vamos detalhar isso um pouco mais.
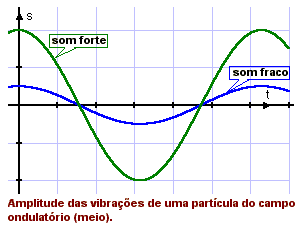
Vale lembrar que, durante a propagação das ondas tem lugar um transporte de energia, no entanto, as partículas do meio não se deslocam no sentido da propagação das ondas, limitando-se a realizar movimentos oscilatórios nas proximidades da posição de equilíbrio (quando a amplitude das ondas é pequena e o meio em que se propagam não é viscoso). A grandeza que é numericamente igual à energia média transportada pela onda, por unidade de tempo, através de uma unidade de área da superfície da onda é denominada intensidade física da onda. Essa intensidade é medida em W/m2. A intensidade das ondas acústicas é denominada intensidade física do som ou, simplesmente, intensidade sonora.
Durante a propagação das ondas mecânicas, a velocidade e a aceleração das partículas do meio variam de acordo com a mesmo tipo da lei do deslocamento (espaço, elongação), ou seja, uma lei harmônica. Quando a 'amplitude' do deslocamento (elongação máxima) das partículas durante a propagação de uma onda harmônica plana de pulsação w apresenta o valor a,
a 'amplitude' máxima da velocidade da oscilação terá o valor vmáx. = w.a
a 'amplitude' máxima da aceleração da oscilação terá o valor gmáx.= w2.a
e a intensidade física da onda será dada por I = (1/2).V.r.w2.a2
onde r é a massa específica do meio onde a onda se propaga, V é a velocidade de propagação.
Como w = 2.p.f e, uma vez que r e V são características do meio elástico, supondo-o homogêneo e à temperatura constante podemos escrever:

I = k.f2.a2

--- para uma dada freqüência, a intensidade física é diretamente proporcional ao quadrado da amplitude;
--- para uma dada amplitude, a intensidade física é diretamente proporcional ao quadrado da freqüência (e isso explica claramente a alta energia transportada por um ultra-som).
O nível de variação da intensidade fisiológica (DS) cuja unidade é o bell (b) e a intensidade física (I) cuja unidade é o W/m2 relacionam-se mediante uma lei experimental ou lei de Weber-Fechner:
A variação da intensidade fisiológica (DS), na zona central do campo de audibilidade é proporcional à variação dos logaritmos das intensidades físicas correspondentes.
Assim, seja So uma intensidade fisiológica de referência e Io a correspondente intensidade física. Se S é outra intensidade fisiológica qualquer e I a intensidade física correspondente, a lei de Weber-Fechner permite escrever:

adotando-se So ==> Io e tomando-se S ==> I vem S - So = log(I/Io), em bell (b).

Exemplo: Numa conversação fraca (conversa baixa), seja I1 = 10 mW/cm2 a intensidade física recebida por um ouvinte. Calcular qual será a variação da intensidade auditiva percebida pelo ouvinte, quando a intensidade da onda sonora da conversação aumentar para I2 = 100 mW/cm2.
Solução: I1 = 10 mW/cm2 ==> S1 e I2 = 100 mW/cm2 ==> S2 , pergunta-se o valor de DS = S2 - S1 ; pomos

DS = log10(I2/I1) = log10(100/10) = log1010 = 1 bell

Comumente, em vez de usarmos o bell como nível de variação de intensidade auditiva, usa-se o decibel, de modo que, podemos por:

DS = S2 - S1 = 10.log10(I2/I1) (db)

Por convenção internacional, definiu-se So= 0, para Io = 10-12 W/m2 como sendo a intensidade auditiva de referência, relativa a um som simples de freqüência 1000 Hz. Essa intensidade corresponde ao limiar de audição.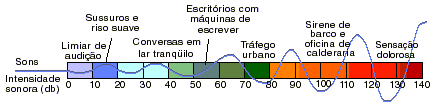

A intensidade do som captada pelo ouvido corresponde à sensação do que se denomina popularmente de volume do som. Quando o som tem uma determinada intensidade mínima, o ouvido humano não capta o som. Essa intensidade mínima é denominada nível mínimo de audição, ou como colocamos acima, limiar de audição e esse mínimo difere segundo a freqüência dos sons. Quando a intensidade é elevada, o som provoca uma sensação dolorosa. A intensidade mínima a que um som ainda provoca sensação dolorosa tem o nome de limiar da sensação dolorosa.
A intensidade auditiva também pode ser referida em fons e, para tanto, basta que se fixe as seguintes referências: freqüência de 1000 Hz; intensidade física de 10-12 W/m2 ==> So = 0 fon. Com essas convenções a lei de Weber-Fechner torna-se:

S (em fons) = 10.log10 (I/10-12), com I em W/m2 .

Exemplo: Sabendo-se que uma onda sonora apresenta intensidade física de 1 W/m2 dizer, em fons, a intensidade auditiva percebida por um observador.
Solução: So = 0 ==> 10-12 W/m2
S = ? ==> 1 W/m2

S = 10.log10(1/10-12) = 10.log101012 = 120 fons

Notas:
a) No ar, o som se propaga, normalmente, sob a forma de ondas esféricas, valendo: I1/I2 = d22/d12 , ou em palavras: a intensidade física da onda diminui com o quadrado da distância à fonte.
b) No ar, o som se propaga, normalmente, sob a forma de ondas esféricas, valendo: a1/a2 = d2/d1 , ou em palavras: a amplitude de vibração das partículas do meio diminui com a distância da partícula considerada à fonte.
A altura do som está ligada unicamente à sua freqüência; é a qualidade pela qual um som grave (som baixo --- freqüência baixa) se distingue de um som agudo (som alto --- freqüência alta).

É fácil perceber que essa característica do som depende tão somente da freqüência; sabe-se, por exemplo, que encurtando-se uma lamina elástica (gilete presa no bordo da mesa), aumenta-se a freqüência de suas vibrações e, correlativamente, constata-se que o som emitido se torna mais e mais agudo.

O quociente das freqüências de dois sons, define um intervalo sonoro (i), em particular, se i = 2, ou seja, f2/f1 = 2, teremos um intervalo de uma oitava — a freqüência do som mais agudo é o dobro da freqüência do outro.
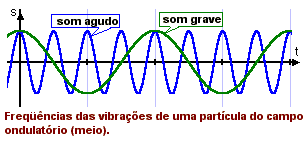
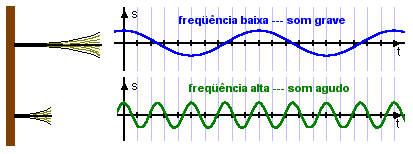
A definição dos diversos intervalos musicais levam ao estabelecimento de uma ESCALA MUSICAL. Em música, usam-se apenas determinados sons, de freqüências convencionais e que se denominam notas musicais. Denomina-se gama ao conjunto das notas musicais pertencentes ao intervalo de uma oitava.

Gama natural de Zarlino

dó1

ré1

mi1

fá1

sol1

lá1

si1

dó2

Intervalos fundamentais:
1°) tom maior = 9/8 ... (f2/f1 = 9/8)2°) tom menor = 10/9 ... (f2/f1 = 10/9)3°) semi-tom = 16/15 ... (f2/f1 = 16/15)

Relação com a tônica (dó1):

1

9/8

5/4

4/3

3/2

5/3

15/8

2

Notas

dó1

ré1

mi1

fá1

sol1

lá1

si1

dó2

Intervalos relativos

9/8

10/9

16/15

9/8

10/9

9/8

16/15

Relação entre notas

24

27

30

32

36

40

45

48

A fim de que os diversos instrumentos musicais possam dar as mesmas notas,foi necessário fixar a altura absoluta de uma certa nota, isto é, sua freqüência. Um congresso internacional fixou:

freqüência do lá3 = 435 Hz

Em musica, utilizam-se nove oitavas, cada uma delas sendo caracterizada por um índice compreendido entre -1 e +9 (não se usa o índice zero): -1__1__2__3__4__5__6__7__8__9.
Cada nota de uma certa oitava (por exemplo ré4) tem freqüência igual ao dobro da nota correspondente da escala anterior (no caso, ré3 ) assim, no exemplo: fré4 = 2.fré3 .
Exemplo: Conhecida a freqüência do lá3 = 435 Hz, determinar a freqüência do si-1.
Solução: Inicialmente deve-se determinar a freqüência do lá-1(que pertence à mesma gama do si-1):

Os limites extremos da voz humana são cerca de 60 e 550 Hz para o homem e 110 e 1300 Hz para a mulher. Imagine a 'incompatibilidade auditiva' que deve existir entre um casal cujo homem fala na base dos 60 Hz e a mulher na base dos 1300 Hz! [Nota: Nos E.U.A. há casos de divórcios baseados em incompatibilidade auditiva.]
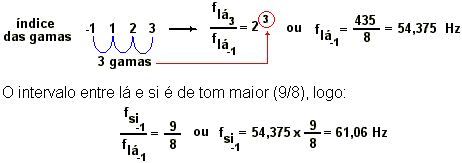
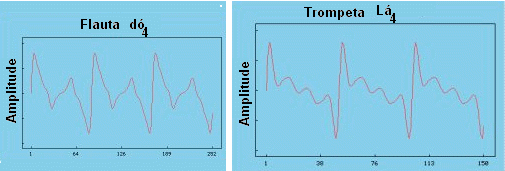
O timbre depende dos harmônicos associados ao som fundamental no caso dos sons musicais ou das ondas que se superpõem, no caso dos sons compostos em geral. No caso dos sons musicais, é a qualidade que permite distinguir dois sons de mesma altura emitidos por fontes sonoras diferentes; uma flauta e um violino, por exemplo, ambos emitindo, digamos, o dó3.
É o número (quantidade) e as intensidades dos harmônicos (que sempre existem ao se tocar um instrumento musical) que acompanham o som fundamental que dão ao som musical essa característica (enfeite) particular.

Abaixo, esquerda, ilustramos a forma de onda denominada dente de serra. O som correspondente é produzido à partir do som fundamental de freqüência f ao qual se superpõem os sons de freqüências 2f, 3f, 4f, ..., respectivamente, com amplitudes 1/2, 1/3, 1/4, ...
Mediante softwares geradores de gráficos de funções, tal curva pode ser posta assim:

f(t)=sin(2·p·440·t)+sin(2·p·880·t)/2+sin(2·p·1320·t)/3+sin(2·p·1760·t)/4+....

Nesse exemplo, a freqüência fundamental é a de 440 Hz. Fazendo 2·p·440·t = x, 2·p·880·t = 2x, etc. a função será: y = f(x) = sinx + (sin2x)/2 + (sin3x)/3 + (sin4x)/4 + ...

Acima, direita, ilustramos a forma de onda denominada onda quadrada. O som correspondente é produzido à partir do som fundamental de freqüência f ao qual se superpõem os sons de freqüências 3f, 5f, 7f, ..., respectivamente, com amplitudes 1/3, 1/5, 1/7, ...
Mediante softwares geradores de gráficos de funções (Equation Grapher), tal curva pode ser posta assim:

f(t)=sin(2·p·440·t)+sin(2·p·1320·t)/3+sin(2·p·2200·t)/5+sin(2·p·3080·t)/7+...

Nesse exemplo, a freqüência fundamental é a de 440 Hz.
Fazendo 2·p·440·t = x, 2·p·1320·t = 3x, etc. a função será: y = f(x) = sin(x) + sin(3x)/3 + sin(5x)/5 + sin(7x)/7 + .. ...

www.algosobre.com.br