Área do triângulo

Considere um triângulo no plano cartesiano de vértices A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C). A área desse triângulo é dada por:

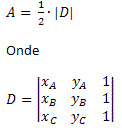
Observe que a área é obtida multiplicando ½ pelo módulo do determinante das coordenadas dos vértices.

Exemplo 1. Determine a área de um triângulo de vértices A(3, 3), B(6, 3) e C(3, 5).
Solução: vamos fazer o cálculo do determinante das coordenas dos vértices do triângulo.


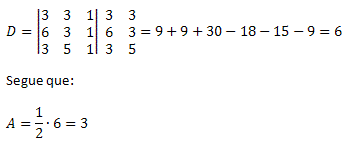
Exemplo 2. Determine o valor de k para que o triângulo de vértices A(0, 0), B(k, 0) e C(0, k) tenha uma área de 32 unidades de área.
Solução: primeiro devemos realizar o cálculo do determinante das coordenadas dos vértices do triângulo. Teremos:



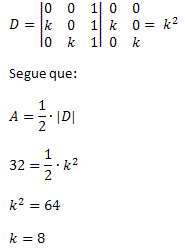
Exemplo 3. Calcule a área do triângulo de vértices A(0, 2), B(8, 6) e C(14, – 8).
Solução: realizando o cálculo do determinante das coordenadas dos vértices dos triângulos, obtemos:

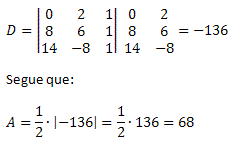
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática