Circunferência

Marcos Noé

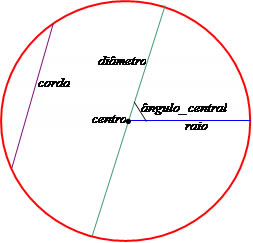
Circunferência e seus elementos

No cotidiano identificamos objetos e construções que lembram uma circunferência, um contorno ou regiões circulares. A circunferência possui propriedades e definições que precisam ser conhecidas na sua utilização. Ela possui alguns elementos como: raio, diâmetro, centro, arco, corda, comprimento e área.

Raio (r): Distância entre o centro e a extremidade da circunferência;

Diâmetro (D): corda que vai de uma extremidade a outra passando pelo centro;

Corda: qualquer reta traçada de uma extremidade a outra;

Ângulo central: ângulo que possui como vértice o centro da circunferência;

Comprimento: medida linear da circunferência;

Área: determina a superfície delimitada pela circunferência;

Arco: parte da circunferência limitada por dois pontos.

Um importante número utilizado nos cálculos envolvendo a circunferência é o π (pi), que resulta da divisão entre o comprimento e o diâmetro da figura circular. O π é um número irracional e vale aproximadamente 3,14. Para calcularmos o comprimento e a área da circunferência utilizamos as respectivas fórmulas matemáticas: C = 2πr e
A = πr².

Exemplo 1

Determine o comprimento de uma praça circular que possui um raio de 10 metros.

C = 2*π*r
C = 2*3,14*10
C = 62,8

O comprimento da praça é de 62,8 metros.

Exemplo 2

Calcule a área da superfície limitada por uma circunferência que possui um raio de 4 metros.
A = π * r²
A = 3,14 * 4²
A = 3,14 * 16
A = 50,24 m²

A área é de aproximadamente 50,24 m²

Exemplo 3

Calcule a área em negrito da figura a seguir, sabendo que o raio da circunferência maior mede 10 cm e o raio da menor é 3 cm.

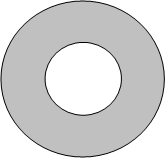
Basta calcularmos a área da circunferência maior e subtrairmos da circunferência menor. Observe:

Área total = πr² – πr²
Área total = 3,14 * 10² – 3,14 * 3²
Área total = 3,14 * 100 – 3,14 * 9
Área total = 314 – 58,26
Área total = 285,74 m²

A área da região demarcada equivale a 285,74 m².