Os estudos em Geometria Analítica possibilitam a relação entre a álgebra e a geometria, abrangendo situações em que são envolvidos ponto, reta e figuras espaciais. Um conceito básico de geometria deve ser aproveitado na GA, a fim de estabelecer a distância entre dois pontos, “por dois pontos passa apenas uma reta”.
Dado o plano cartesiano, vamos estabelecer a distância entre os pontos A e B.
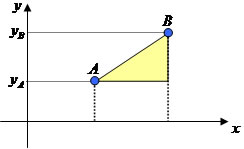
Podemos observar que os pontos possuem coordenadas, sendo o ponto A(xa,ya) e B(xb,yb), note a formação do triângulo retângulo ABC, onde os lados BC: cateto, AC: cateto e AB: hipotenusa.
Verificamos que a distância entre os pontos A e B é a hipotenusa do triângulo retângulo, que pode ser calculada aplicando o Teorema de Pitágoras. Com o auxílio da álgebra e de conhecimentos geométricos podemos generalizar e construir uma fórmula que determine a distância entre dois pontos no plano, conhecendo suas coordenadas.
Cateto BC: yb – yaCateto AC: xb – xa
Hipotenusa AB: distância (D)
Pelo Teorema de Pitágoras temos: “o quadrado da hipotenusa é igual à soma dos quadrados dos catetos”
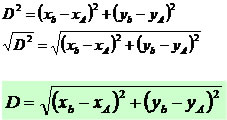
Exemplo 1
Dados os pontos A (2,-3) e B (4,5), determine a distância entre eles.
xa: 2
xb: 4
ya: -3
yb: 5
Dado o plano cartesiano, vamos estabelecer a distância entre os pontos A e B.

Podemos observar que os pontos possuem coordenadas, sendo o ponto A(xa,ya) e B(xb,yb), note a formação do triângulo retângulo ABC, onde os lados BC: cateto, AC: cateto e AB: hipotenusa.
Verificamos que a distância entre os pontos A e B é a hipotenusa do triângulo retângulo, que pode ser calculada aplicando o Teorema de Pitágoras. Com o auxílio da álgebra e de conhecimentos geométricos podemos generalizar e construir uma fórmula que determine a distância entre dois pontos no plano, conhecendo suas coordenadas.
Cateto BC: yb – yaCateto AC: xb – xa
Hipotenusa AB: distância (D)
Pelo Teorema de Pitágoras temos: “o quadrado da hipotenusa é igual à soma dos quadrados dos catetos”
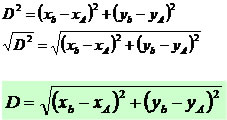
Exemplo 1
Dados os pontos A (2,-3) e B (4,5), determine a distância entre eles.
xa: 2
xb: 4
ya: -3
yb: 5
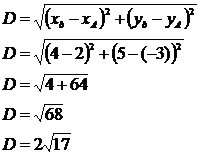
Exemplo 2
Calcule a distância entre os pontos P(-2,3) e Q(-5,-9).
xa: -2
xb: -5
ya: 3
yb: -9
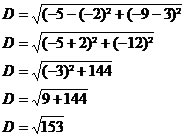
www.mundoeducacao.com.br
Nenhum comentário:
Postar um comentário